卷积-CNN-GCN-LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation论文笔记
参考博客:https://www.zhihu.com/question/54504471/answer/332657604
1. 卷积
连续: ( f ∗ g ) ( n ) = ∫ − ∞ + ∞ f ( τ ) g ( n − τ ) d t (f*g)(n)=\int_{-\infty}^{+\infty}f(\tau)g(n-\tau)dt (f∗g)(n)=∫−∞+∞f(τ)g(n−τ)dt
离散: ( f ∗ g ) ( n ) = ∑ τ = − ∞ + ∞ f ( τ ) g ( n − τ ) (f*g)(n)=\sum_{\tau=-\infty}^{+\infty}f(\tau)g(n-\tau) (f∗g)(n)=∑τ=−∞+∞f(τ)g(n−τ)
其中 g ( n − τ ) g(n-\tau) g(n−τ) 作翻转——卷,平移 n 个单位;让两个函数对应点相乘,然后相加——积。
应用场景
1. 信号分析
f ( t ) ⟶ f(t)\longrightarrow f(t)⟶单位冲击响应函数 g ( t ) g(t) g(t)
卷积的结果不仅跟当前时刻输入信息的响应值有关,也跟过去所有时刻输入信号的响应值都有关系。考虑了对过去所有输入的效果累积。
2. 图像处理
f ( x , y ) ⟶ f(x,y)\longrightarrow f(x,y)⟶单位冲击响应函数 g ( x , y ) g(x,y) g(x,y)
在图像处理中,卷积处理的结果其实就是把每个像素同边的,甚至是整个图像的像素都考虑进来,对当前像素进行某种加权处理(GCN 中的邻域聚合就是从这演变来的?)。
“积”:全局概念,把两个函数在时间/空间上进行混合。
为什么要“卷”?
施加一种约束, τ + ( n − τ ) = n \tau+(n-\tau)=n τ+(n−τ)=n
例如:丢两个骰子,求总和为 4 的概率。约束条件:点数和,相当于上面的 n。
图像处理例子(一维信号到二维图像)
【一幅图】 ⟹ [ a 00 a 01 ⋯ a 0 n a 10 a 11 ⋯ a 1 n ⋮ ⋮ ⋱ ⋮ a m 0 a m 1 ⋯ a m n ] \Longrightarrow \left[\begin{array}{cccc} a_{00} & a_{01} & \cdots & a_{0n}\\ a_{10} & a_{11} & \cdots & a_{1n}\\ \vdots & \vdots & \ddots & \vdots\\ a_{m0} & a_{m1} & \cdots & a_{mn}\\ \end{array}\right] ⟹⎣⎢⎢⎢⎡a00a10⋮am0a01a11⋮am1⋯⋯⋱⋯a0na1n⋮amn⎦⎥⎥⎥⎤
对图像的处理函数(如平滑、边缘提取)
g = [ b − 1 , − 1 b − 1 , 0 b − 1 , 1 b 0 , − 1 b 0 , 0 b 0 , 1 b 1 , − 1 b 1 , 0 b 1 , 1 ] g=\left[\begin{array}{ccc} b_{-1,-1} & b_{-1,0} & b_{-1,1}\\ b_{0,-1} & b_{0,0} & b_{0,1}\\ b_{1,-1} & b_{1,0} & b_{1,1}\\ \end{array}\right] g=⎣⎡b−1,−1b0,−1b1,−1b−1,0b0,0b1,0b−1,1b0,1b1,1⎦⎤
( f ∗ g ) ( u , v ) = ∑ i ∑ j f ( i , j ) g ( u − i , v − j ) = ∑ i ∑ j a i , j ⋅ b u − i , v − j (f*g)(u,v)=\sum_i\sum_jf(i,j)g(u-i,v-j)=\sum_i\sum_j a_{i,j}\cdot b_{u-i,v-j} (f∗g)(u,v)=∑i∑jf(i,j)g(u−i,v−j)=∑i∑jai,j⋅bu−i,v−j
f = [ a u − 1 , v − 1 a u − 1 , v a u − 1 , v + 1 a u . v − 1 a u , v a u , v + 1 a u + 1 , v − 1 a u + 1 , v a m n ] f=\left[\begin{array}{ccc} a_{u-1,v-1} & a_{u-1,v} & a_{u-1,v+1}\\ a_{u.v-1} & a_{u,v} & a_{u,v+1}\\ a_{u+1,v-1} & a_{u+1,v} & a_{mn}\\ \end{array}\right] f=⎣⎡au−1,v−1au.v−1au+1,v−1au−1,vau,vau+1,vau−1,v+1au,v+1amn⎦⎤
g ′ = [ b 1 , 1 b 1 , 0 b 1 , − 1 b 0 , 1 b 0 , 0 b 0 , − 1 b − 1 , 1 b − 1 , 0 b − 1 , − 1 ] g^{'} =\left[\begin{array}{ccc} b_{1,1} & b_{1,0} & b_{1,-1}\\ b_{0,1} & b_{0,0} & b_{0,-1}\\ b_{-1,1} & b_{-1,0} & b_{-1,-1}\\ \end{array}\right] g′=⎣⎡b1,1b0,1b−1,1b1,0b0,0b−1,0b1,−1b0,−1b−1,−1⎦⎤
( f ∗ g ′ ) ( u , v ) = a u − 1 , v − 1 ⋅ b 1 , 1 + a u − 1 , v ⋅ b 1 , 0 + a u − 1 , v + 1 ⋅ b 1 , − 1 + a u , v − 1 ⋅ b 0 , 1 + a u , v ⋅ b 0 , 0 + a u , v + 1 ⋅ b 0 , − 1 + a u + 1 , v − 1 ⋅ b − 1 , 1 + a u + 1 , v ⋅ b − 1 , 0 + a u + 1 , v + 1 ⋅ b − 1 , − 1 (f*g^{'})(u,v)=a_{u-1,v-1}\cdot b_{1,1} + a_{u-1,v}\cdot b_{1,0} + a_{u-1,v+1}\cdot b_{1,-1} + a_{u,v-1}\cdot b_{0,1} + a_{u,v}\cdot b_{0,0} + a_{u,v+1}\cdot b_{0,-1} + a_{u+1,v-1}\cdot b_{-1,1} + a_{u+1,v}\cdot b_{-1,0} + a_{u+1,v+1}\cdot b_{-1,-1} (f∗g′)(u,v)=au−1,v−1⋅b1,1+au−1,v⋅b1,0+au−1,v+1⋅b1,−1+au,v−1⋅b0,1+au,v⋅b0,0+au,v+1⋅b0,−1+au+1,v−1⋅b−1,1+au+1,v⋅b−1,0+au+1,v+1⋅b−1,−1
a, b 下标之和都是 (u,v),是对这种加权求和的一种约束,这也是为什么要将矩阵 g 翻转的原因(其实是不需要翻转的,因为这个卷积核的参数是训练出来的,它自动会训练出翻转后的矩阵)
g 越大,涉及同边像素越多;g 设计不同,模糊/锐利
[ 1 9 1 9 1 9 1 9 1 9 1 9 1 9 1 9 1 9 ] \left[ \begin{array}{ccc} \frac{1}{9} & \frac{1}{9} & \frac{1}{9}\\ \frac{1}{9} & \frac{1}{9} & \frac{1}{9}\\ \frac{1}{9} & \frac{1}{9} & \frac{1}{9} \end{array}\right] ⎣⎡919191919191919191⎦⎤ / [ − 1 − 1 − 1 − 1 9 − 1 − 1 − 1 − 1 ] \left[ \begin{array}{ccc} -1 & -1 & -1\\ -1 & 9 & -1\\ -1 & -1 & -1\\ \end{array}\right] ⎣⎡−1−1−1−19−1−1−1−1⎦⎤
2. CNN
离散卷积本质就是一种加权求和: ( f ∗ g ) ( n ) = ∑ τ = − ∞ + ∞ f ( τ ) g ( n − τ ) (f*g)(n)=\sum_{\tau=-\infty}^{+\infty}f(\tau)g(n-\tau) (f∗g)(n)=∑τ=−∞+∞f(τ)g(n−τ);其中, g ( n − τ ) g(n-\tau) g(n−τ) 相当于权重。
CNN 中卷积的本质上就是利用一个共享参数的过滤器,通过计算中心像素点以及相邻像素点的加权和来构成 feature map,实现空间特征提取。
卷积核的系数如何确定?
随机化初值,然后根据误差函数 loss 通过反向传播梯度下降进行迭代优化。
CNN 到 GCN 关键点:卷积核的参数通过优化求出才能实现特征提取的作用。
GCN 理论很大一部分工作就是为了引入可以优化的卷积参数 h ^ ( λ l ) \hat{h}(\lambda_l) h^(λl).
互相关
f ( x ) ⊗ g ( x ) = ∫ f ∗ ( x ′ − x ) h ( x ′ ) d x ′ f(x)\otimes g(x)= \int f^*(x^{'}-x)h(x^{'})dx^{'} f(x)⊗g(x)=∫f∗(x′−x)h(x′)dx′
所以说 CNN 是在提取图像的每个局部(感受野)范围和卷积核的互相关函数。
数学中“卷积核”都是已知或给定的;卷积神经网络中“卷积核”本来就是要训练的参数,不是给定的。
3. GCN
CNN 是欧几里得(Euclidean)结构:CV、NLP
GCN 是非欧结构:社交网络、信息网络(图论中抽象意义上的拓扑图)
谱聚类(spectral clustering)
相较于传统 k-means 对数据分布的适应性更强。
1. 概述:(从图论中演化出来的)
主要思想:把所有数据看作空间中的点,这些点之间可以用边连接起来,distance 越远,边权重越小。通过对所有数据点组成的图进行切图,让切图后不同子图间边权重和尽可能小,子图内边权重和尽可能大,从而达到聚类目的。
2. k-means(关键 k)
参考链接:https://zhuanlan.zhihu.com/p/78798251?utm_source=qq
例子:为了让每个村民到其最近中心点距离和最小。
步骤:
- 随机选取 k 个初始聚类中心点;
- 计算每个村民到每个聚类中心点的距离,选取最近的聚类中心点;
- 针对每个聚类中心点,重新计算每个中心聚类中心点的位置(该类中各村民位置质心);
- 重复上面 2、3 两步操作,直到达到某个中止条件(迭代次数、最小误差变化等)。
3. 核 k-means 算法
针对非凸的数据分布形状时可以引入核函数来优化。
核聚类方法的主要思想是:通过一个非线性映射,将输入空间的数据点映射到高维的特征空间中,并在新的特征空间中进行聚类,非线性映射增加了数据点线性可分的概率。
图: G ( V , E ) G(V, E) G(V,E)
GCN 要为除 CV、NLP 之外的任务提供一种处理、研究的模型。
拉普拉斯矩阵: L = D − M L=D-M L=D−M(其中 D 是度矩阵,M 是相似矩阵)
4. Spectral graph theory: 借助于图的拉普拉斯矩阵的特征值和特征向量来研究图的性质
L = D − A L = D - A L=D−A:对称、半正定、 0 ⩽ λ 1 ⩽ λ 2 ⩽ ⋯ 0\leqslant \lambda_1\leqslant\lambda_2\leqslant\cdots 0⩽λ1⩽λ2⩽⋯
δ T L δ = 1 2 ∑ i ∑ j w i j ( d i − d j ) 2 \delta^T L \delta=\frac{1}{2}\sum_i\sum_jw_{ij}(d_i-d_j)^2 δTLδ=21∑i∑jwij(di−dj)2
其中 L 为拉普拉斯矩阵,Graph Fourier Transformation 及 Graph Convolution 的定义都要用到。
GCN 本质:用来提取拓扑图的空间特征。
- vertex domain(spatial domain)
- spectral domian: 借助图谱的理论来实现拓扑图上的卷积操作
- 定义 Graph 上的 Fourier Transformation(傅里叶变换);
- 进而定义 convolution;
- 与 DL 结合,Graph Convolution Network。
常见拉普拉斯矩阵:
- L = D − A L = D-A L=D−A
- (vol) L s y s = D − 1 2 L D − 1 2 = D − 1 2 ( D − A ) D − 1 2 L^{sys}=D^{-\frac{1}{2}}LD^{-\frac{1}{2}} =D^{-\frac{1}{2}}(D-A)D^{-\frac{1}{2}} Lsys=D−21LD−21=D−21(D−A)D−21
- L r w = D − 1 L = D − 1 ( D − A ) L^{rw}=D^{-1}L=D^{-1}(D-A) Lrw=D−1L=D−1(D−A)
为什么 GCN 要用到 Laplace Matrix?
- L 对称,可以进行特征分解(谱分解),这就和 GCN 的 spectral domain 对应上了;
- Laplace Matrix 只在中心顶点和一阶相连的顶点上(1-hop neighbor)有非 0 元素;
- 通过 Laplace 算子与 Laplace Matrix 进行类比,Laplace Matrix 就是图上的 Laplace 算子 Δ \Delta Δ
- (矢量) ∇ f = ( ∂ f ∂ x , ∂ f ∂ y , ∂ f ∂ z ) = ∂ f ∂ x i → + ∂ f ∂ y j → + ∂ f ∂ z k → \nabla f=(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z}) =\frac{\partial f}{\partial x}\overrightarrow{i}+\frac{\partial f}{\partial y}\overrightarrow{j}+\frac{\partial f}{\partial z}\overrightarrow{k} ∇f=(∂x∂f,∂y∂f,∂z∂f)=∂x∂fi+∂y∂fj+∂z∂fk,其中 ∇ f = ∂ ∂ x i → + ∂ ∂ y j → + ∂ ∂ z k → \nabla f =\frac{\partial}{\partial x}\overrightarrow{i}+\frac{\partial}{\partial y}\overrightarrow{j}+\frac{\partial}{\partial z}\overrightarrow{k} ∇f=∂x∂i+∂y∂j+∂z∂k称为(三维)向量的微分算子。
- (标量)散度 divergence: “ ∇ ⋅ " “\nabla\cdot" “∇⋅"。
- 拉普拉斯算子 Laplace Operator 是 n 维欧几里得空间中一个二阶微分算子,定义为梯度( ∇ f \nabla f ∇f)的散度( ∇ ⋅ \nabla\cdot ∇⋅), Δ f = ∇ 2 f = ∇ ⋅ ∇ f = d i v ( g r a d f ) \Delta f=\nabla^2f=\nabla\cdot\nabla f=div(grad~f) Δf=∇2f=∇⋅∇f=div(grad f)。
笛卡尔坐标系下的表示法:
Δ f = ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 + ∂ 2 f ∂ z 2 \Delta f=\frac{\partial^2f}{\partial x^2}+\frac{\partial^2f}{\partial y^2}+\frac{\partial^2f}{\partial z^2} Δf=∂x2∂2f+∂y2∂2f+∂z2∂2f
n 维: Δ = ∑ i ∂ 2 ∂ x i 2 \Delta=\sum_i\frac{\partial^2}{\partial x_i^2} Δ=∑i∂xi2∂2
下面推导离散函数的导数: ∂ f ∂ x = f ′ ( x ) = f ( x + 1 ) − f ( x ) \frac{\partial f}{\partial x}=f^{'}(x)=f(x+1)-f(x) ∂x∂f=f′(x)=f(x+1)−f(x)
∂ 2 f ∂ x 2 = f ′ ′ ( x ) ≈ f ′ ( x + 1 ) − f ′ ( x ) = f ( x + 1 ) − f ( x ) − f ( x ) + f ( x − 1 ) \frac{\partial^2 f}{\partial x^2}=f^{''}(x)\approx f^{'}(x+1)-f^{'}(x)=f(x+1)-f(x)-f(x)+f(x-1) ∂x2∂2f=f′′(x)≈f′(x+1)−f′(x)=f(x+1)−f(x)−f(x)+f(x−1)
将 Laplace 算子 " Δ " "\Delta" "Δ"也转化为离散形式:

Δ f = ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 = f ( x + 1 , y ) + f ( x − 1 , y ) − 2 f ( x , y ) + f ( x , y + 1 ) + f ( x , y − 1 ) − 2 f ( x , y ) = f ( x + 1 , y ) + f ( x − 1 , y ) + f ( x , y + 1 ) + f ( x , y − 1 ) − 4 f ( x , y ) \Delta f=\frac{\partial^2 f}{\partial x^2}+ \frac{\partial^2 f}{\partial y^2}=f(x+1,y)+f(x-1,y)-2f(x,y)+f(x,y+1)+f(x,y-1)-2f(x,y)\\ =f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y) Δf=∂x2∂2f+∂y2∂2f=f(x+1,y)+f(x−1,y)−2f(x,y)+f(x,y+1)+f(x,y−1)−2f(x,y)=f(x+1,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)−4f(x,y)
下面用散度的概念来解读:
Δ f > 0 \Delta f>0 Δf>0 表示该点有发散通量的正源(发散源)
Δ f < 0 \Delta f<0 Δf<0 表示该点有吸收通量的正源(洞或汇)
Δ f = 0 \Delta f=0 Δf=0 无点源
【另一角度】Laplace 算子计算周围点与中心点的梯度差。
现在将该结论推广到图上:
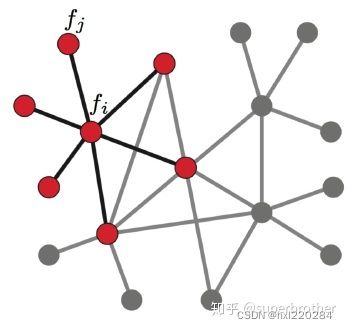
无向无权图: Δ f i = ∑ j ∈ N i ( f i − f j ) \Delta f_i=\sum_{j\in N_i}(f_i-f_j) Δfi=∑j∈Ni(fi−fj)
【疑问】不是应该 f j − f i f_j-f_i fj−fi 吗??
无向有权图: Δ f i = ∑ j ∈ N i w i j ( f i − f j ) = ∑ j ∈ N w i j ( f i − f j ) = ∑ j ∈ N w i j f i − ∑ j ∈ N w i j f j = d i f i − w i : f \Delta f_i=\sum_{j\in N_i}w_{ij}(f_i-f_j)=\sum_{j\in N}w_{ij}(f_i-f_j)=\sum_{j\in N}w_{ij}f_i-\sum_{j\in N}w_{ij}f_j=d_if_i-w_{i:}f Δfi=∑j∈Niwij(fi−fj)=∑j∈Nwij(fi−fj)=∑j∈Nwijfi−∑j∈Nwijfj=difi−wi:f
其中 w i : = ( w i 1 , ⋯ , w i N ) , f = ( f 1 ⋮ f N ) w_{i:}=(w_{i1},\cdots,w_{iN}), f=\left(\begin{array}{c} f_1 \\ \vdots \\ f_N \end{array}\right) wi:=(wi1,⋯,wiN),f=⎝⎜⎛f1⋮fN⎠⎟⎞
之所以第二个等号可以这样简化是因为: j ∈ N i w i j ≠ 0 ; j ∉ N i w i j = 0 j\in N_i~w_{ij}\neq 0;j\notin N_i~w_{ij}=0 j∈Ni wij=0;j∈/Ni wij=0
Δ f = ( Δ f 1 ⋮ Δ f N ) = ( d 1 f 1 − w 1 : f ⋮ d N f N − w N : f ) = ( d 1 ⋱ d N ) f − ( w 1 : ⋮ w N : ) f = d i a g ( d i ) f − W f = ( D − W ) f = L f \Delta f=\left(\begin{array}{c} \Delta f_1 \\ \vdots \\ \Delta f_N \end{array}\right) =\left(\begin{array}{c} d_1f_1-w_{1:}f \\ \vdots \\ d_Nf_N-w_{N:}f \end{array}\right) =\left(\begin{array}{ccc} d_1 & & \\ & \ddots & \\ & & d_N \end{array}\right)f -\left(\begin{array}{c} w_{1:} \\ \vdots \\ w_{N:} \end{array}\right)f =diag(d_i)f-Wf=(D-W)f=Lf Δf=⎝⎜⎛Δf1⋮ΔfN⎠⎟⎞=⎝⎜⎛d1f1−w1:f⋮dNfN−wN:f⎠⎟⎞=⎝⎛d1⋱dN⎠⎞f−⎝⎜⎛w1:⋮wN:⎠⎟⎞f=diag(di)f−Wf=(D−W)f=Lf
Laplace Matrix(半正定、对称、正交矩阵)一定可以谱分解:
L = U ( λ 1 ⋱ λ N ) U − 1 = U ( λ 1 ⋱ λ N ) U T ( U ⋅ U T = E ) L=U\left(\begin{array}{ccc} \lambda_1 & & \\ & \ddots & \\ & & \lambda_N \\ \end{array}\right)U^{-1} =U\left(\begin{array}{ccc} \lambda_1 & & \\ & \ddots & \\ & & \lambda_N \\ \end{array}\right)\quad U^T(U\cdot U^T=E) L=U⎝⎛λ1⋱λN⎠⎞U−1=U⎝⎛λ1⋱λN⎠⎞UT(U⋅UT=E)
**如何从传统的傅里叶变换及卷积 类比到 Graph 上的傅里叶变换及卷积?
核心工作就是把 Laplace 算子的特征函数 e − i w t e^{-iwt} e−iwt (与特征值 λ l \lambda_l λl有关)变成 Graph 对应的 Laplace Matrix 的特征向量 ∑ i u l ∗ ( i ) \sum_i u_l^*(i) ∑iul∗(i)
先搞懂傅里叶变换
参考链接:https://zhuanlan.zhihu.com/p/19763358
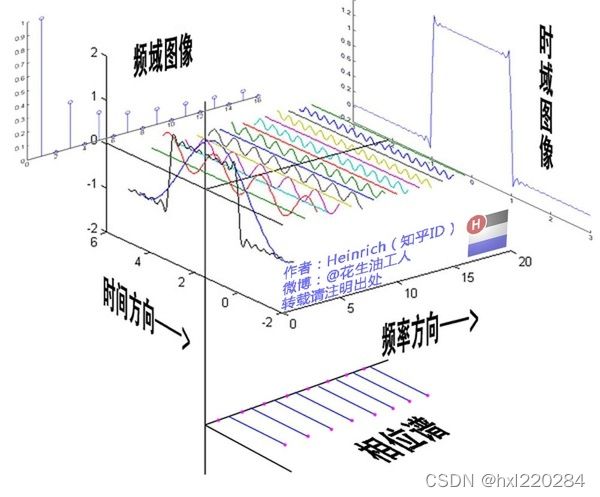
时域:世界都是以时间贯穿的
频域:世界是永恒不变的
F ( ω ) = F [ f ( t ) ] = ∫ f ( t ) e − i ω t d t F(\omega)=\mathcal{F}[f(t)]=\int f(t)e^{-i\omega t}dt F(ω)=F[f(t)]=∫f(t)e−iωtdt
任何周期函数,都可以看作是不同振幅,不同相位正弦波(cos)的叠加
傅里叶分析:
- 傅里叶级数(Fourier Serie)
- 傅里叶变换(Fourier Transformation)
(频谱是从侧面看的,相位谱是从下面看的)
很多在时域看似不可能做到的数学操作,在频域相反很容易。这就是需要傅里叶变换的地方:
- 从某条曲线中去除一些特定的频率成分——滤波;
- 求解微分方程:傅里叶变换可以让微分和积分在频域中变为乘法和除法。
虚数 i:乘虚数 i 的其中一个功能——旋转。
复数的物理意义:旋转、信号可拆分可合并(实数和虚数)
e i x = cos x + i sin x e^{ix}=\cos x+i\sin x eix=cosx+isinx——将正弦波统一成了简单的指数形式!
传统傅里叶变换定义
F ( ω ) = F [ f ( t ) ] = ∫ f ( t ) e − i w t d t , Δ e − i w t = − ω 2 e − i w t F(\omega)=\mathcal{F}[f(t)]=\int f(t)e^{-iwt}dt,\Delta e^{-iwt}=-\omega^2 e^{-iwt} F(ω)=F[f(t)]=∫f(t)e−iwtdt,Δe−iwt=−ω2e−iwt
拉普拉斯矩阵就是离散拉普拉斯算子。
离散积分就是一种内积形式:
F ( λ l ) = f ^ ( λ l ) = ∑ i = 1 N f ( i ) u l ∗ ( i ) , u l ∗ ( i ) F(\lambda_l)=\hat{f}(\lambda_l)=\sum_{i=1}^Nf(i)u_l^*(i),u_l^*(i) F(λl)=f^(λl)=∑i=1Nf(i)ul∗(i),ul∗(i)第 l l l 个特征向量的第 i i i 个分量
⟹ f ^ = U T ⋅ f \Longrightarrow \hat{f}=U^T\cdot f ⟹f^=UT⋅f
Graph 上的傅里叶逆变换
F − 1 [ F ( ω ) ] = 1 2 π ∫ F ( ω ) e i ω t d ω \mathcal{F}^{-1}[F(\omega)]=\frac{1}{2\pi}\int F(\omega)e^{i\omega t}d\omega F−1[F(ω)]=2π1∫F(ω)eiωtdω
迁移到 Graph 上变为对特征值 λ l \lambda_l λl 求和:
f ( i ) = ∑ l = 1 N f ^ ( λ l ) u l ( i ) ⟹ f = U ⋅ f ^ f(i)=\sum_{l=1}^N\hat{f}(\lambda_l)u_l(i)\Longrightarrow f=U\cdot \hat{f} f(i)=∑l=1Nf^(λl)ul(i)⟹f=U⋅f^
推广卷积
卷积定理:函数卷积的傅里叶变换是函数傅里叶变换的乘积,即对于函数 f(t) 与 g(t) 两者的卷积是其函数傅里叶变换乘积的逆变换。
【个人理解】为什么这里的卷积要涉及到拉普拉斯矩阵、傅里叶变换这些复杂的知识,说白了就是为了卷积的时候能简便计算嘛,毕竟天下没有免费的午餐!
f ∗ g = F [ f ^ ( ω ) ⋅ g ^ ( ω ) ] = 1 2 π ∫ f ^ ( ω ) ⋅ g ^ ( ω ) e i ω t d ω f*g=\mathcal{F}[\hat{f}(\omega)\cdot \hat{g}(\omega)]=\frac{1}{2\pi}\int \hat{f}(\omega)\cdot \hat{g}(\omega)e^{i\omega t}d\omega f∗g=F[f^(ω)⋅g^(ω)]=2π1∫f^(ω)⋅g^(ω)eiωtdω
( f ∗ g ) G = U ( h ^ ( λ 1 ) ⋱ h ^ ( λ n ) ) U T f ( 1 ) (f*g)_G= U\left(\begin{array}{ccc} \hat{h}(\lambda_1) & & \\ & \ddots & \\ & & \hat{h}(\lambda_n) \end{array}\right)U^Tf\quad (1) (f∗g)G=U⎝⎛h^(λ1)⋱h^(λn)⎠⎞UTf(1)
【我的疑惑】???上面这个公式是怎么得到的
很多论文: ( f ∗ g ) G = U ( ( U T h ) ⊙ ( U T f ) ) ( 2 ) (f*g)_G=U((U^Th)\odot (U^Tf))\quad (2) (f∗g)G=U((UTh)⊙(UTf))(2)
在 GCN 中的 local connectivity 和 parameter share
CNN 两大核心思想:
- 网络局部连接
- 卷积核参数共享
卷积中:1. 拉普拉斯矩阵 2. 切比雪夫多项式
y ^ = σ ( U g θ ( Λ ) U T x ) \hat{y}=\sigma(Ug_{\theta}(\Lambda)U^Tx) y^=σ(Ugθ(Λ)UTx)
其中共享参数的 kernel—— g θ ( Λ ) g_{\theta}(\Lambda) gθ(Λ)集中求法:
- 第一代: g θ ( Λ ) = ( θ 1 ⋱ θ N ) g_{\theta}(\Lambda) =\left(\begin{array}{ccc} \theta_1 & & \\ & \ddots & \\ & & \theta_N \\ \end{array}\right) gθ(Λ)=⎝⎛θ1⋱θN⎠⎞
- 第二代: g θ ( Λ ) = ( ∑ j = 0 K α j λ 1 j ⋱ ∑ j = 0 K α j λ N j ) = ∑ j = 0 K α j Λ j g_{\theta}(\Lambda) =\left(\begin{array}{ccc} \sum_{j=0}^K \alpha_j \lambda_1^j & & \\ & \ddots & \\ & & \sum_{j=0}^K \alpha_j \lambda_N^j \\ \end{array}\right) =\sum_{j=0}^K \alpha_j \Lambda^j gθ(Λ)=⎝⎜⎛∑j=0Kαjλ1j⋱∑j=0KαjλNj⎠⎟⎞=j=0∑KαjΛj
那么 y ^ = σ ( ∑ j = 0 K α j L j x ) \hat{y}=\sigma(\sum_{j=0}^K \alpha_j L^jx) y^=σ(∑j=0KαjLjx)
第二代相较于第一代,参数复杂度降低了,神奇般的不用做特征分解了,直接用拉普拉斯矩阵进行变换!
Chebyshev 多项式作为 GCN 卷积核
y ^ = σ ( U g θ ( Λ ) U T x ) \hat{y}=\sigma(Ug_{\theta}(\Lambda)U^Tx) y^=σ(Ugθ(Λ)UTx)
其中,U 为 Laplace Matrix 特征向量构建的矩阵,g 为卷积核,x 为输入特征。
利用 Chebyshev 多项式代替卷积核:
g θ ( Λ ) = ∑ k = 0 K − 1 β k T k ( Λ ~ ) g_\theta(\Lambda)=\sum_{k=0}^{K-1}\beta_kT_k(\tilde{\Lambda}) gθ(Λ)=k=0∑K−1βkTk(Λ~)
其中, T k ( ⋅ ) T_k(\cdot) Tk(⋅) 是 k 阶Chebyshev 多项式, β k \beta_k βk 是系数(迭代更新的参数), Λ ~ \tilde{\Lambda} Λ~ re-scale 特征值对角矩阵,进行这个变换是因为 Chebyshev 多项式输入要在 [-1, 1] 之间。
T k ( x ) = cos ( k ⋅ arccos ( x ) ) T_k(x)=\cos(k\cdot \arccos(x)) Tk(x)=cos(k⋅arccos(x))
如何转化?
- Λ ⩾ 0 ⇒ λ ⩾ 0 \Lambda\geqslant0 \Rightarrow \lambda\geqslant 0 Λ⩾0⇒λ⩾0,除以 λ m a x ⇒ [ 0 , 1 ] \lambda_{max}\Rightarrow [0,1] λmax⇒[0,1];
- 2 ∗ [ 0 , 1 ] − 1 ⇒ [ − 1 , 1 ] 2*[0,1]-1\Rightarrow [-1,1] 2∗[0,1]−1⇒[−1,1]。
Λ ~ = 2 Λ / λ m a x − I \tilde{\Lambda}=2\Lambda/\lambda_{max}-I Λ~=2Λ/λmax−I
y ^ = σ ( U ∑ k = 0 K − 1 β k T k ( Λ ~ ) U T x ) \hat{y}=\sigma(U\sum_{k=0}^{K-1}\beta_kT_k(\tilde{\Lambda})U^Tx) y^=σ(Uk=0∑K−1βkTk(Λ~)UTx)
因为 Chebyshev 多项式作用在对角线矩阵上,不会影响矩阵运算:
y ^ = σ ( ∑ k = 0 K − 1 β k T k ( U Λ ~ U T ) x ) = σ ( ∑ k = 0 K − 1 β k T k ( L ~ ) x ) \\\hat{y}=\sigma(\sum_{k=0}^{K-1}\beta_kT_k(U\tilde{\Lambda}U^T)x)=\sigma(\sum_{k=0}^{K-1}\beta_kT_k(\tilde{L})x) y^=σ(k=0∑K−1βkTk(UΛ~UT)x)=σ(k=0∑K−1βkTk(L~)x)
上式成立是因为: L = U Λ U T L=U\Lambda U^T L=UΛUT
T k ( L ~ ) = 2 L ~ T k − 1 ( L ~ ) − T k − 2 ( L ~ ) , T 0 ( L ~ ) = I , T 1 ( L ~ ) = L ~ T_k(\tilde{L})=2\tilde{L}T_{k-1}(\tilde{L})-T_{k-2}(\tilde{L}),T_0(\tilde{L})=I,T_1(\tilde{L})=\tilde{L} Tk(L~)=2L~Tk−1(L~)−Tk−2(L~),T0(L~)=I,T1(L~)=L~
L ~ = 2 L / λ m a x − I = 2 ( D − A ) / λ m a x − I \tilde{L}=2L/\lambda_{max}-I=2(D-A)/\lambda_{max}-I L~=2L/λmax−I=2(D−A)/λmax−I
用上述公式的好处是:无需再进行特征向量的分解。
4. LightGCN
阅读文献:LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation
论文链接:https://dl.acm.org/doi/pdf/10.1145/3397271.3401063?casa_token=QacjOy9WaZ4AAAAA:b0XAc7XJ4_0E3775ptzFotL-xpN0AszulUYGBtDDO7V85QTzob6M5NfSQ_1lMZX1Pa2v0CogdQXp
代码链接:
- https://github.com/kuandeng/LightGCN
- https://github.com/gusye1234/pytorch-light-gcn
目的
GCN 最开始是为了图分类任务而设计的,不完全适用于推荐系统。本文的目标是简化 GCN 的设计,只包含 GCN 中的重要组件——邻域聚合,并使用在所有层上学习到的嵌入的加权和作为最终嵌入(而不是采用最后一层/将所有层拼接起来)。
方法
LightGCN,在 NGCF 模型上做了简化和改进。
结果
本文的方法有显著提升(平均大约在 16% 的相对改进),从分析和实证两方面进一步分析简单 LightGCN 的合理性。
① 介绍
NGCF:
- 特征转换(W1, W2)
- 邻域聚合
- 非线性激活( σ ( ⋅ ) \sigma(\cdot) σ(⋅))
从 GCN 那里继承来的,最初适用于属性图上的节点分类,每个节点都有丰富的属性作为输入特征;而 CF 中,每个节点(user,item)只由一个除了作为标识符之外,没有具体语义的 one-hot 表示的 ID 描述。
而多层非线性特征转换的过程,不会带来任何好处,反而会增加模型训练难度。
对 NGCF 进行消融研究:1、3 两个操作对 NGCF 有效性没有贡献,删除它们可以显著提高准确度。
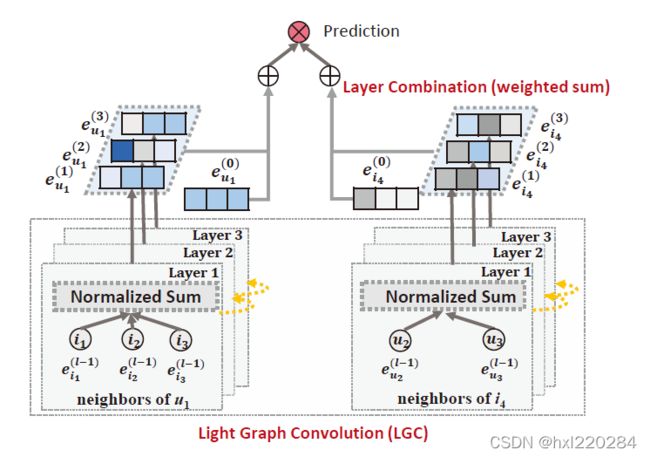
因此提出了新的模型 LightGCN:在将每个用户/项目与 ID 嵌入关联后,我们在用户-项目交互图上传播嵌入以及改进它们。然后将不同传播层的嵌入信息与加权和结合,得到最终的预测嵌入信息。
② 准备工作
1. NGCF
e → u ( k + 1 ) = σ ( W 1 e → u ( k ) + ∑ i ∈ N u 1 ∣ N u ∣ ⋅ ∣ N i ∣ ( W 1 e → i ( k ) + W 2 ( e → i ( k ) ⊙ e → u ( k ) ) ) ) \overrightarrow{e}_u^{(k+1)}=\sigma(W_1\overrightarrow{e}_u^{(k)}+\sum_{i\in \mathcal{N}_u}\frac{1}{\sqrt{|\mathcal{N}_u|\cdot|\mathcal{N}_i}|}(W_1\overrightarrow{e}_i^{(k)}+W_2(\overrightarrow{e}_i^{(k)}\odot \overrightarrow{e}_u^{(k)}))) eu(k+1)=σ(W1eu(k)+i∈Nu∑∣Nu∣⋅∣Ni∣1(W1ei(k)+W2(ei(k)⊙eu(k))))
e → i ( k + 1 ) = σ ( W 1 e → i ( k ) + ∑ u ∈ N i 1 ∣ N u ∣ ⋅ ∣ N i ∣ ( W 1 e → u ( k ) + W 2 ( e → u ( k ) ⊙ e → i ( k ) ) ) ) \overrightarrow{e}_i^{(k+1)}=\sigma(W_1\overrightarrow{e}_i^{(k)}+\sum_{u\in \mathcal{N}_i}\frac{1}{\sqrt{|\mathcal{N}_u|\cdot|\mathcal{N}_i}|}(W_1\overrightarrow{e}_u^{(k)}+W_2(\overrightarrow{e}_u^{(k)}\odot \overrightarrow{e}_i^{(k)}))) ei(k+1)=σ(W1ei(k)+u∈Ni∑∣Nu∣⋅∣Ni∣1(W1eu(k)+W2(eu(k)⊙ei(k))))
N u \mathcal{N}_u Nu:用户 u 交互过的项目集, N i \mathcal{N}_i Ni:交互过项目 i 的用户集,W1 和 W2 是可训练的权重,矩阵在每一层执行特征转换。通过传播 L 层,NGCF 获得 L+1 个嵌入来描述一个用户 ( e → u ( 0 ) , e → u ( 1 ) , ⋯ , e → u ( L ) ) (\overrightarrow{e}_u^{(0)},\overrightarrow{e}_u^{(1)},\cdots,\overrightarrow{e}_u^{(L)}) (eu(0),eu(1),⋯,eu(L)) 和一个项目 ( e → i ( 0 ) , e → i ( 1 ) , ⋯ , e → i ( L ) ) (\overrightarrow{e}_i^{(0)},\overrightarrow{e}_i^{(1)},\cdots,\overrightarrow{e}_i^{(L)}) (ei(0),ei(1),⋯,ei(L));然后串联起 ( e → i ( 0 ) ∣ ∣ e → i ( 1 ) ∣ ∣ ⋯ ∣ ∣ e → i ( L ) ) (\overrightarrow{e}_i^{(0)}||\overrightarrow{e}_i^{(1)}||\cdots||\overrightarrow{e}_i^{(L)}) (ei(0)∣∣ei(1)∣∣⋯∣∣ei(L))以获得最终的用户嵌入和项目嵌入,并使用内积生成预测分数。
2. NGCF 实证探索
- NGCF-f:删除了 W1 和 W2 的特征转换;
- NGCF-n:消除了非线性激活函数;
- NGCF-fn:去掉了特征变换矩阵和非线性激活函数。
【数据集】Gowalla 和 Amazon-Book 神经网络为 2 层设置
【结论】
- 特征变换会对 NGCF 产生负面影响;
- 加入非线性激活函数,对(W1,W2)存在的情况下影响较小,但禁用(W1,W2)时影响较大;
- 从整体上看,特征变换和非线性激活函数对 NGCF 的影响十分负面。
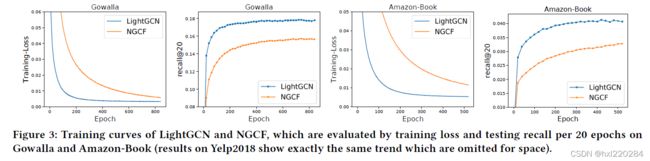
通过绘制了训练损失函数和测试 recall 的模型状态曲线,可以得出结论:NGCF 的恶化是由于训练困难,而不是过度拟合导致的。
③ LightGCN 模型
模型简单的好处:
- 更具解释性;
- 易于训练和维护;
- 易于分析模型行为并对其修改。
1. LightGCN
GCN 的基本思想:通过在图上平滑特征来学习节点的表示,即执行图的卷积。
邻域聚合可以抽象为: e → u ( k + 1 ) = A G G ( e → u ( k ) , { e → i ( k ) : i ∈ N u } ) \overrightarrow{e}_u^{(k+1)}=AGG(\overrightarrow{e}_u^{(k)},\{\overrightarrow{e}_i^{(k)}:i\in \mathcal{N}_u\}) eu(k+1)=AGG(eu(k),{ei(k):i∈Nu})
AGG 是一个聚合函数,是图数据卷积的——考虑第 k 层对目标节点及其邻居节点的表示。
2. 轻量图卷积(LGC):
e → u ( k + 1 ) = ∑ i ∈ N u 1 ∣ N u ∣ ⋅ ∣ N i ∣ e → i ( k ) \overrightarrow{e}_u^{(k+1)}=\sum_{i\in \mathcal{N}_u}\frac{1}{\sqrt{|\mathcal{N}_u|\cdot|\mathcal{N}_i}|}\overrightarrow{e}_i^{(k)} eu(k+1)=i∈Nu∑∣Nu∣⋅∣Ni∣1ei(k)
e → i ( k + 1 ) = ∑ u ∈ N i 1 ∣ N u ∣ ⋅ ∣ N i ∣ e → u ( k ) \overrightarrow{e}_i^{(k+1)}=\sum_{u\in \mathcal{N}_i}\frac{1}{\sqrt{|\mathcal{N}_u|\cdot|\mathcal{N}_i}|}\overrightarrow{e}_u^{(k)} ei(k+1)=u∈Ni∑∣Nu∣⋅∣Ni∣1eu(k)
【注】在 LGC 中,只聚合已连接的邻居,而不集成目标节点本身(self-connection),下一小节中介绍的层组合操作本质上捕获了与自连接相同的效果。因此 LGC 不需要包含自连接。
3. 层组合和模型预测
e → u = ∑ k = 0 K α k e → u ( k ) ; e → i = ∑ k = 0 K α k e → i ( k ) \overrightarrow{e}_u=\sum_{k=0}^K\alpha_k\overrightarrow{e}_u^{(k)};\quad \overrightarrow{e}_i=\sum_{k=0}^K\alpha_k\overrightarrow{e}_i^{(k)} eu=k=0∑Kαkeu(k);ei=k=0∑Kαkei(k) ( α k ≥ 0 \alpha_k\geq 0 αk≥0为第 k 层嵌入的权重)
这里的 α k \alpha_k αk 统一为 KaTeX parse error: Expected '}', got 'EOF' at end of input: \frac{1}{K+1性能较好。
y ^ u i = e → u T e → i \hat{y}_{ui}=\overrightarrow{e}_u^T\overrightarrow{e}_i y^ui=euTei 作为推荐生成的排名分数。
4. 矩阵形式
R ∈ R M × N R\in \mathbb{R}^{M\times N} R∈RM×N
邻接矩阵: A = ( 0 R R T 0 ) A= \left(\begin{array}{cc} \textbf{0} & R\\ R^T & \textbf{0} \end{array}\right) A=(0RTR0) A 对称!!
E ( 0 ) ∈ R ( M + N ) × T T : e m b e d d i n g s i z e E^{(0)}\in \mathbb{R}^{(M+N)\times T}\quad T:embedding~size E(0)∈R(M+N)×TT:embedding size
E ( k + 1 ) = ( D − 1 / 2 A D − 1 / 2 ) E ( k ) E^{(k+1)}=(D^{-1/2}AD^{-1/2})E^{(k)} E(k+1)=(D−1/2AD−1/2)E(k)
因此用于模型的嵌入矩阵: E = α 0 E ( 0 ) + α 1 E ( 1 ) + ⋯ α K E ( K ) = α 0 E ( 0 ) + α 1 A ~ E ( 0 ) + ⋯ α K A ~ K E ( 0 ) E=\alpha_0 E^{(0)}+\alpha_1 E^{(1)}+\cdots \alpha_K E^{(K)}=\alpha_0 E^{(0)}+\alpha_1 \tilde{A}E^{(0)}+\cdots \alpha_K\tilde{A}^K E^{(0)} E=α0E(0)+α1E(1)+⋯αKE(K)=α0E(0)+α1A~E(0)+⋯αKA~KE(0)
其中 A ~ = D − 1 / 2 A D − 1 / 2 \tilde{A}=D^{-1/2}AD^{-1/2} A~=D−1/2AD−1/2 对称归一化矩阵。
5. 模型分析
1. SGCN:
通过消除非线性和将多个权重矩阵压缩为一个权重矩阵来简化 GCN。
E ( k + 1 ) = ( D + I ) − 1 / 2 ( A + I ) ( D + I ) − 1 / 2 E ( k ) E^{(k+1)}=(D+I)^{-1/2}(A+I)(D+I)^{-1/2}E^{(k)} E(k+1)=(D+I)−1/2(A+I)(D+I)−1/2E(k)
+ I +I +I 表示添加了自连接。
下面分析中省略了 ( D + I ) − 1 / 2 (D+I)^{-1/2} (D+I)−1/2 ,因为它只是重新缩放嵌入。
E ( K ) = ( A + I ) E ( K − 1 ) = ( A + I ) K E ( 0 ) = ( K 0 ) E ( 0 ) + ( K 1 ) A E ( 0 ) + ( K 2 ) A 2 E ( 0 ) + ⋯ + ( K K ) A K E ( 0 ) E^{(K)}=(A+I)E^{(K-1)}=(A+I)^{K}E^{(0)} =\left(\begin{array}{c}K\\0\end{array}\right)E^{(0)} +\left(\begin{array}{c}K\\1\end{array}\right)AE^{(0)} +\left(\begin{array}{c}K\\2\end{array}\right)A^2E^{(0)} +\cdots +\left(\begin{array}{c}K\\K\end{array}\right)A^KE^{(0)} E(K)=(A+I)E(K−1)=(A+I)KE(0)=(K0)E(0)+(K1)AE(0)+(K2)A2E(0)+⋯+(KK)AKE(0)
上面推导表明,在 A 中插入自连接并在其上传播嵌入,本质上等于在每个 LGC 层上传播的嵌入的加权和。
【SGCN 中的 (A+I) 等价于 LightGCN 中 A & 各层权重的加权和】
2. APPNP(GCN 与个性化的 PageRank 联系起来)
可以长期传播,不会有过平滑的风险。
E ( k + 1 ) = β E ( 0 ) + ( 1 − β ) A ~ E ( k − 1 ) = ⋯ = β E ( 0 ) + β ( 1 − β ) A ~ E ( 0 ) + β ( 1 − β ) 2 A ~ 2 E ( 0 ) + ⋯ + ( 1 − β ) K A ~ K E ( 0 ) E^{(k+1)}=\beta E^{(0)}+(1-\beta)\tilde{A}E^{(k-1)}=\cdots=\beta E^{(0)}+\beta(1-\beta)\tilde{A}E^{(0)}+\beta(1-\beta)^2\tilde{A}^2E^{(0)}+\cdots+(1-\beta)^K\tilde{A}^KE^{(0)} E(k+1)=βE(0)+(1−β)A~E(k−1)=⋯=βE(0)+β(1−β)A~E(0)+β(1−β)2A~2E(0)+⋯+(1−β)KA~KE(0)
调整 α k \alpha_k αk,LightGCN 完全可以恢复 APPNP 的预测嵌入。
3. 二阶嵌入平滑(以用户为例,第二层平滑了交互项目上有重叠的用户)
e → u ( 2 ) = ∑ i ∈ N u 1 ∣ N u ∣ ⋅ ∣ N i ∣ e → i ( 1 ) = ∑ i ∈ N u ( 1 ∣ N i ∣ ∑ v ∈ N i 1 ∣ N u ∣ ⋅ ∣ N v ∣ ) e → v ( 0 ) \overrightarrow{e}_u^{(2)}=\sum_{i\in \mathcal{N}_u}\frac{1}{\sqrt{|\mathcal{N}_u|\cdot|\mathcal{N}_i}|}\overrightarrow{e}_i^{(1)}=\sum_{i\in \mathcal{N}_u}(\frac{1}{|\mathcal{N}_i|}\sum_{v\in \mathcal{N}_i}\frac{1}{\sqrt{|\mathcal{N}_u|\cdot|\mathcal{N}_v}|})\overrightarrow{e}_v^{(0)} eu(2)=i∈Nu∑∣Nu∣⋅∣Ni∣1ei(1)=i∈Nu∑(∣Ni∣1v∈Ni∑∣Nu∣⋅∣Nv∣1)ev(0)
c v → u = 1 ∣ N u ∣ ⋅ ∣ N v ∣ ∑ i ∈ N u ∩ N i 1 ∣ N i ∣ c_{v\rightarrow u}=\frac{1}{\sqrt{|\mathcal{N}_u|\cdot|\mathcal{N}_v}|}\sum_{i\in \mathcal{N}_u\cap \mathcal{N}_i}\frac{1}{|\mathcal{N}_i|} cv→u=∣Nu∣⋅∣Nv∣1i∈Nu∩Ni∑∣Ni∣1
通过这个系数可以解释二阶邻居 v → u v\rightarrow u v→u 影响如下:
- 共同交互项目越多,影响越大;
- 交互项目受欢迎程度越低(这点更能体现用户个性化偏好)影响越大;
- 用户 v 活跃度越低,影响越大。
【在 item 中类似】
6. 模型训练
LightGCN 可训练参数只有第 0 层的嵌入,说明模型复杂度与 MF 相同。
- 采用 BPR 损失(成对损失);
- Adam 优化器,以 mini-batch 的方式使用它;
dropout,因为 LightGCN 中没有特征变换权重矩阵,因此在嵌入层上强制 L2 正则化足以防过拟合;{ α k } k = 0 K \{\alpha_k\}_{k=0}^K {αk}k=0K 学习/用一个注意力网络参数化的技术,可能因为训练数据不包含足够的信号的到可以泛化到位置数据的好处。
④ 实验
Gowalla 和 Amazon-Book 与 NGCF 中完全相同,增加了 Yelp2018 数据集。
评估指标:recall@20,ndcg@20。
所有不与用户交互的项都是候选项。
1. 比较方法
NGCF 已经比 1. 基于 GCN 的 GC-MC 和 PinSage 模型;2. 基于神经网络的 NeuMF 和 CMF;3. 基于 MF 和 HOP-Rec 的方法好。
在 NGCF 的基础上,进一步对比了两种相关且具有竞争力的 CF 方法:
- Mult-VAE:是一个基于变分自动编码器(VAE)的 item-CF 方法,假定数据有一个多项式分布生成的,并使用变分推论进行参数估计;
- GRMF:通过加入图拉普拉斯正则化因子来平滑 MF,BPR 损失函数:
L = − ∑ u = 1 U ( ∑ j ∉ N u l n σ ( e → u T e → i + e → u T e → j ) + λ g ∣ ∣ e → u − e → i ∣ ∣ 2 ) + λ ∣ ∣ E ∣ ∣ 2 L=-\sum_{u=1}^U(\sum_{j\notin\mathcal{N}_u}ln\sigma(\overrightarrow{e}_u^T\overrightarrow{e}_i+\overrightarrow{e}_u^T\overrightarrow{e}_j)+\lambda_g||\overrightarrow{e}_u-\overrightarrow{e}_i||^2)+\lambda||E||^2 L=−u=1∑U(j∈/Nu∑lnσ(euTei+euTej)+λg∣∣eu−ei∣∣2)+λ∣∣E∣∣2
- GRMF-norm: λ g ∣ ∣ e → u ∣ N u ∣ − e → i ∣ N i ∣ ∣ ∣ 2 \lambda_g||\frac{\overrightarrow{e}_u}{\sqrt{|\mathcal{N}_u|}}-\frac{\overrightarrow{e}_i}{\sqrt{|\mathcal{N}_i|}}||^2 λg∣∣∣Nu∣eu−∣Ni∣ei∣∣2 变体
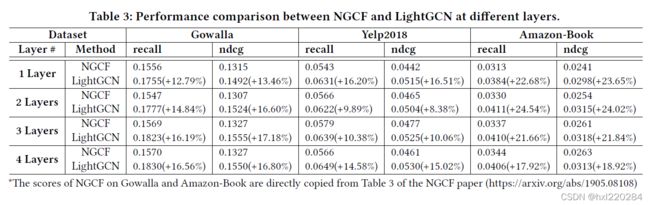
2. 与 NGCF 的性能比较
图 3 绘制了训练损失和测试 recall 的训练曲线。
- 在所有情况下,LightGCN 的性能都比 NGCF 要好;
- 增加层的数量可以提高性能,但收益会减少;
- LightGCN 损失更低,测试精度更好,说明泛化性能更好。
3. 和最先进方法的性能比较
LightGCN > Mult-VAE > GRMF/NGCF > MF
GRMF-norm > GRMF
4. 消融和有效性分析
① 层组合
- LightGCN-Single(只用最后一层 E k E_k Ek):层数从 1-4 增加时,性能先提升后下降,大多数情况峰值点在第二层;
- LightGCN:性能随层数的增加而提高,证明“层组合”处理过平滑的有效性;
- 在 Gowalla 数据集上 LightGCN 表现优于 LightGCN-Single,另外两个数据集都不是这样,还没对 α k \alpha_k αk 进行调优。
② 对称开根归一化:
分别测试了只使用左侧 1 ∣ N u ∣ \frac{1}{\sqrt{|\mathcal{N}_u|}} ∣Nu∣1,右侧 1 ∣ N i ∣ \frac{1}{\sqrt{|\mathcal{N}_i|}} ∣Ni∣1归一化,也测试了 L1 正则化(移除平方根)
- 最好的设置是两边都使用开根号标准化;
- 第二好的设置是 LightGCN-L1-L,等价于邻接矩阵按度归一化为一个随机矩阵???
- L1 归一化会降低性能。
③ 定义用户嵌入的平滑度
S u = ∑ u = 1 M ∑ v = 1 M c v → u ( e → u ∣ ∣ e → u ∣ ∣ 2 − e → v ∣ ∣ e → v ∣ ∣ 2 ) 2 S_u=\sum_{u=1}^M\sum_{v=1}^M c_{v\rightarrow u}(\frac{\overrightarrow{e}_u}{||\overrightarrow{e}_u||^2}-\frac{\overrightarrow{e}_v}{||\overrightarrow{e}_v||^2})^2 Su=u=1∑Mv=1∑Mcv→u(∣∣eu∣∣2eu−∣∣ev∣∣2ev)2
其中 c v → u = 1 ∣ N u ∣ ⋅ ∣ N v ∣ ∑ i ∈ N u ∩ N i 1 ∣ N i ∣ c_{v\rightarrow u}=\frac{1}{\sqrt{|\mathcal{N}_u|\cdot|\mathcal{N}_v}|}\sum_{i\in \mathcal{N}_u\cap \mathcal{N}_i}\frac{1}{|\mathcal{N}_i|} cv→u=∣Nu∣⋅∣Nv∣1∑i∈Nu∩Ni∣Ni∣1
MF 是用 E ( 0 ) E^{(0)} E(0) 进行模型预测的,LightGCN-Single 是用 E ( 2 ) E^{(2)} E(2) 进行模型预测的,说明通过对轻量图卷积(???),使得嵌入变得更平滑,更适合推荐。
5. 超参数研究
对于 L2 正则化系数 λ \lambda λ, λ = 0 \lambda=0 λ=0 比 NGCF+dropout 效果还要好。
⑤ 相关工作
- CF
- GNN:早期研究在谱域上定义了图卷积(例如 Laplace 矩阵分解,Chebyshev 多项式),计算开销很大。之后,GraphSage、GCN 在空间域重新定义了图的卷积,即聚合邻域的嵌入,以细化目标节点的嵌入,具有可解释性和高效性。之后有了 GC-MC,PinSage,NGCF。