支持向量机(Support Vector Machine,SVM)
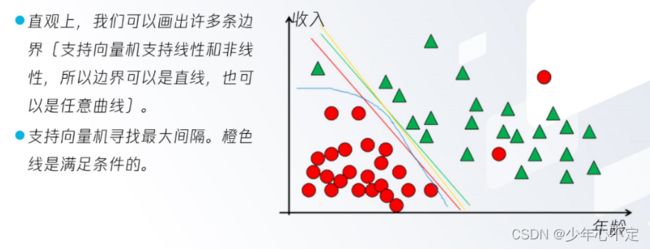
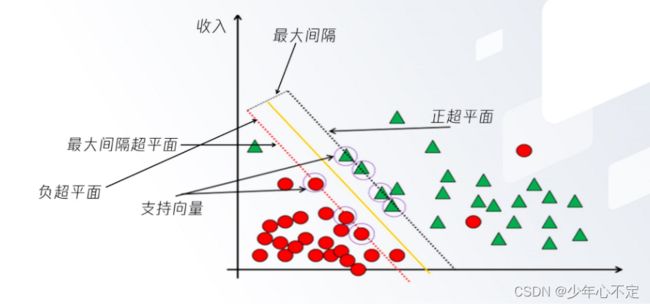
支持向量机是一种基于统计学习理论的模式识别方法。SVM的目的是为了找到一个超平面,使得它能够尽可能多的将两类数据点正确的分开,同时使分开的两类数据点距离分类面最远。为了达到该目的,通常构造一个在约束条件下的优化问题,通过求解该问题,从而得到一个分类器。
支持向量机倾向给出把握程度更高的预测结果,也就是说最终通过支持向量机的计算出的预测结果其实就是一个概率,从中选出预测结果最高的作为最终结果。
支持向量机学习方法包含构建由简至繁的模型:线性支持向量机、线性可分支持向量机及非线性支持向量机。
支持向量机在众多的机器学习算法中以良好的性能立足于机器学习领域。如果不考虑集成学习的算法,不考虑特定的数据集特性问题,在分类算法的模型评估中SVM是表现最好的。SVM是一个二分类算法,他支持线性分类和非线性分类。通过不断演变,SVM也可以支持多元分类,经过扩展,也可以运用于回归问题。
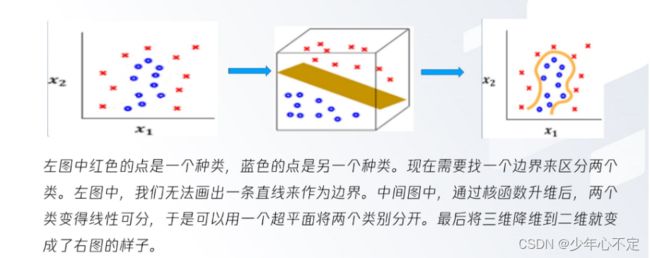
核函数(kernel Function):表示将输入从输入空间映射到特征空间得到特征向量之间的内积。
实例讲解:
鸢尾花数据准备:
from Sklearn.datasets import load_iris
import pandas as pd
iris = load_iris()
data = pd.DataFrame(iris.data,columns = ['花瓣长度','花瓣宽度','花萼长度','花萼宽度'])
data['类别'] = iris.target
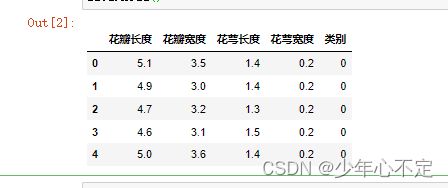
data.head()数据处理:
import matplotlib.pyplot as plt
#检查是否有空数据
for i in range(data.columns.size):
col = data.columns[i]
data[data[col].isnull()]
data.head() #无空数据,将不空的数据显示出来,发现与原数据相同
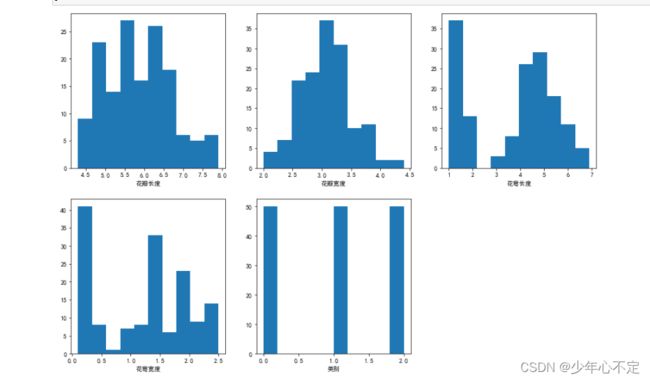
直方图展示各个维度上数据的分布:
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
plt.figure(figsize=(15,10))
for i in range(data.columns.size):
plt.subplot(2,3,i+1)
col = data.columns[i]
plt.hist(data[col])
plt.xlabel(col)
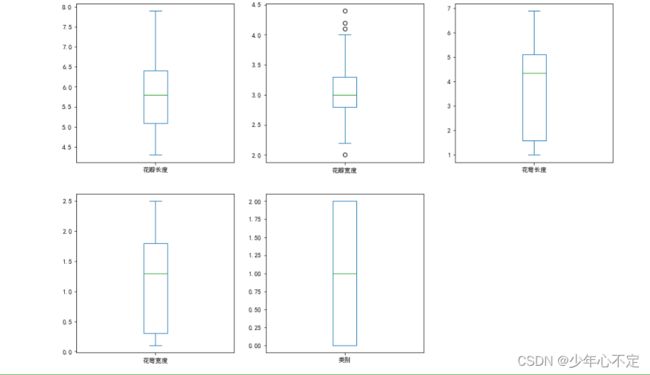
plt.show()通过箱型图探索每个维度上是否具有异常值
plt.figure(figsize=(15,10))
for i in range(data.columns.size):
plt.subplot(2,3,i+1)
col = data.columns[i]
data[col].plot(kind = 'box')
plt.show()数据清洗异常值:
def dealdf(data):
deal = pd.Series().index
for col in data.columns:
s=data[col]
a=s.describe()
high=a['75%']+(a['75%']-a['25%'])*1.5
low =a['25%']-(a['75%']-a['25%'])*1.5
abn = s[(s>high)|(s划分数据集:
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(data,data['类别'],test_size=0.2,random_state=0)
支持向量机的分类:
from sklearn.svm import SVC
svc = SVC() #建立模型
svc.fit(X_train,y_train) #训练模型
svc.score(X_test,y_test) #模型评估
svc.predict(X_test) #输出测试集分类结果