【数据结构C语言版本】手把手教你实现二叉树的非递归前中后序遍历 (附完整代码)
目录
- 写在前面
-
- 1.递归前序遍历
-
-
- 三句话实现递归前序遍历,我是一个精通人性的好代码!
- 1.1 原理,从递归遍历说起
-
- 1.1.1. 不撞NULL不回头
- 1.1.2. 你妈喊你回家吃饭啦
- 1.2 先序递归遍代码实现
- 1.3 手把手带您分析递归前序遍历算法
- 1.4 脑对脑带您分析递归前序遍历代码
-
- 2.非递归遍历
-
- 引言
-
- 透过现象看本质,如何手动实现递归的重复调用、访问打印与回溯?
- 2.1 前序遍历
-
- 2.1.1 先序遍历非递归代码实现
- 2.1.2 手把手带您分析非递归前序算法
- 2.1.3 脑对脑带您分析非递归前序代码
- 2.2 中序遍历
-
- 2.2.1 中序遍历非递归代码实现
- 2.2.2 手把手带您分析非递归中序算法
- 2.2.3 脑对脑带您分析非递归中序代码
- 2.3 后序遍历
-
- 2.3.1 后序遍历非递归代码实现
- 2.3.2 手把手带您分析非递归后序算法
- 2.3.3 脑对脑带您分析非递归后序代码
- 2.4 简易后序遍历
-
- 2.4.1 原理
- 2.4.2 算法分析
- 2.4.3 代码实现
- 附录 (完整代码实现)
写在前面
1.递归前序遍历
三句话实现递归前序遍历,我是一个精通人性的好代码!
1.1 原理,从递归遍历说起
1.1.1. 不撞NULL不回头
我们应明确,DLR的遍历法则需要运用到每一个结点上,即当用根结点访问到其左孩子结点后,其左孩子成为新的根结点,我们重新根据DLR顺序访问其左孩子的左孩子…如此重复,直到某左孩子结点没有它的左孩子,这才完成了DLR中对L的遍历访问。
此时此刻,我们停留在了二叉树最左端的叶子结点。
1.1.2. 你妈喊你回家吃饭啦
假设一位妈妈有两个孩子,开饭时妈妈能叫老大吃饭,必定也能叫老二吃饭。同理,能通过D结点遍历访问左孩子,必能通过D结点访问右孩子。
第一步结束后,我们对左孩子的访问结束,接下来我们通过该左孩子的D结点,去访问D结点的右孩子,对D结点的右孩子使用DLR法则进行左右子树的遍历,到这里,我们完成了三个结点的最小二叉树单元的前序遍历。接着,我们再找到当前D结点的D结点,再通过当前D结点的D结点找到右孩子,对D结点当前D结点的D结点的右孩子使用DLR法则进行左右子树的遍历…如是重复,从最左端的叶子结点处进行回溯
1.2 先序递归遍代码实现
//先序递归
void PreOrder1(BTreeNode *b)
{
if(b!=NULL){
printf("%c",b->data); //访问根结点并打印
PreOrder1(b->lchild); //遍历处理左孩子
PreOrder1(b->rchild); //遍历处理左孩子
}
}
1.3 手把手带您分析递归前序遍历算法
1.4 脑对脑带您分析递归前序遍历代码
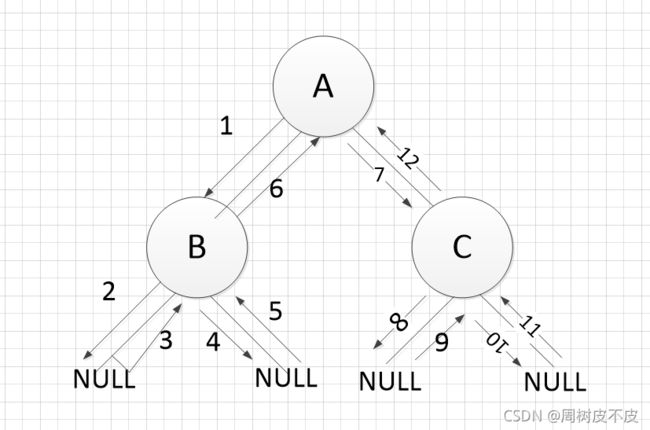
正所谓“大道至简,知易行难,知行合一,得到功成”。为了让读者深入理解前序遍历优美的C语言三行诗,Joe树皮建立了一棵A(B,C)的简单小树带读者一同把玩把玩。
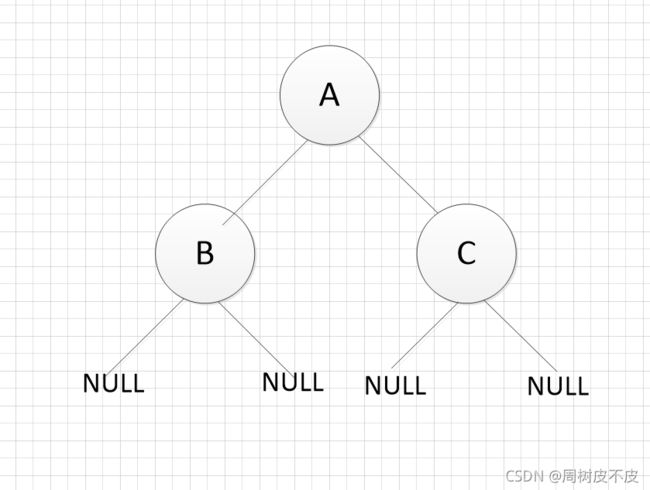
调用PreOrder1(b)
当前b为A结点,当前实参为A结点
printf("%c",b->data);直接访问打印A结点的值
调用PreOrder1(b->lchild);访问到B结点
当前b为A结点,当前实参为B结点
printf("%c",b->data);直接访问打印B结点的值
调用PreOrder1(b->lchild);访问到NULL
当前b为B结点,当前实参为NULL
本次调用结束
调用PreOrder1(b->rchild);访问到NULL
当前b为B结点,当前实参为NULL
本次调用结束
完成对B的DLR
调用PreOrder1(b->rchild);访问到C结点
完成对A的DLR
当前b为A结点,当前实参为C结点
printf("%c",b->data);直接访问打印C结点的值
调用PreOrder1(b->lchild);访问到NULL
当前b为C结点,当前实参为NULL
本次调用结束
调用PreOrder1(b->rchild);访问到NULL
当前b为C结点,当前实参为NULL
本次调用结束
完成对C的DLR
2.非递归遍历
引言
透过现象看本质,如何手动实现递归的重复调用、访问打印与回溯?
1)重复相同的操作,毫无疑问,在代码中我们应使用while、for之类的循环语句实现。
2)而对于访问,通过之前分析我们不难发现,这实则是将D结点、L结点、R结点按照规定顺序依次存进一片连续的存储单元。3)还需明确一个关系:当前孩子结点是下一个的根结点,当前根结点是上一个孩子结点,将此关系映射到数组内发现这两个结点在数组中位于相邻存储单元,因此我们可借数组解决回溯的问题。
回忆之前学习的数据结构知识,什么是运用数组对元素进行基本操作?我们不妨大胆猜想------栈 !
按照这个思路继续分析下去,我们会发现:1)依次将元素存储进数组正是 入栈操作;2)当前访问的结点位于栈顶,我们将其打印后出栈,这正是取栈顶操作。3)每轮循环取栈顶操作之后,新的栈顶元素成为它按DLR顺序进栈的前一个结点,通过取栈顶操作,我们完成了对新栈顶元素R结点的回溯。4)除上述外,我们还需注意栈特有的先进后出的特点,在入栈操作时,先输出的应后入栈。
到这里,我想读者应该能明白:对二叉树的非递归操作,是通过栈的基本操作实现的。
2.1 前序遍历
2.1.1 先序遍历非递归代码实现
//先序非递归
void PreOrder2(BTreeNode *b)
{
SqStack *s; //创建虚拟栈
StackInit(&s);
BTreeNode *TopNode; //用于读取栈顶元素结点
BTreeNode *PNode; //用于读取目标操作结点
if(b!=NULL){
//(1)根结点进栈
//直接操作
/*
s->top++;
s->ST[s->top]=b;
*/
//Push函数操作
Push(&s,&b);
//栈不为空循环进行
while(s->top>-1){
//(2)取栈顶元素(D结点)
//直接操作
/*
TopNode=s->ST[s->top];
s->top--;
printf("%c",TopNode->data);
*/
//调用GetTop函数
printf("%c",GetTop(&s,&TopNode)->data);
//因栈是先入后出 故DLR需先Push右子树再Push左子树
//(3)通过TopNode处理右子树 Push
if(TopNode->rchild!=NULL){
//直接操作
/*
s->top++;
s->ST[s->top]=TopNode->rchild;
*/
//调用Push函数
PNode=TopNode->rchild;
Push(&s,&PNode);
}
//(4)通过TopNode处理左子树 Push
if(TopNode->lchild!=NULL){
//直接操作
/*
s->top++;
s->ST[s->top]=TopNode->lchild;
*/
//调用Push函数
PNode=TopNode->lchild;
Push(&s,&PNode);
}
}
}
printf("\n");
StackDestory(&s);
}
2.1.2 手把手带您分析非递归前序算法
Step1:创建树A(B(D,E),C(,F))
(若无特殊声明,此后前中后序遍历都研究这棵树)
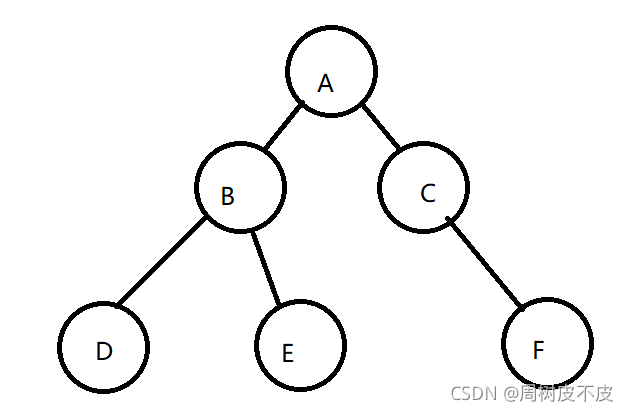
Step2:初始化虚拟栈(前中后序都需要初始化栈操作,故此操作在之后的中后序算法分析里省略)

Step3:手工操作实现先序遍历过程

打印结果:ABDECF
2.1.3 脑对脑带您分析非递归前序代码
原理:先打印根结点的值,因栈是先入后出,根据DLR顺序得知需先右子树入栈再左子树入栈。
(1)根结点进栈
(栈Push 操作:top指针++,通过top指针控制ST数组下标存入根结点)
while(栈空)
{
(2)栈顶元素出栈并打印
(栈GetTop操作:当前栈顶元素出栈打印,top指针–)
(3)PNode指向当前栈顶元素以进行后续(4)(5)操作
(4)处理右子树
(栈Push 操作:右结点进栈,top指针++,通过top指针控制ST数组下标存入右结点。)
(5)处理左子树
(栈Push 操作:左结点进栈,top指针++,通过top指针控制ST数组下标存入左结点。)
}
}
(声明:栈操作的具体实现在中后序代码分析中省略)
2.2 中序遍历
2.2.1 中序遍历非递归代码实现
//中序非递归
void MidOrder2(BTreeNode *b)
{
SqStack *s; //创建虚拟栈
StackInit(&s);
BTreeNode *TopNode; //用于读取栈顶元素结点
BTreeNode *PNode; //用于读取目标操作结点
if(b!=NULL){
PNode=b;
//栈不为空或者当前结点不为空循环继续
while(s->top>-1||PNode!=NULL){
//(1)左孩子遍历进栈
while(PNode!=NULL){
/*
s->top++;
s->ST[s->top]=PNode;
*/
Push(&s,&PNode);
PNode=PNode->lchild;
}
//(2)栈顶结点的右孩子为空可直接出栈
/*
TopNode=s->ST[s->top];
s->top--;
*/
printf("%c",GetTop(&s,&TopNode)->data);
//(3)若不为空则访问右孩子 进入while循环进栈
PNode=TopNode->rchild;
}
}
printf("\n");
StackDestory(&s);
}
2.2.2 手把手带您分析非递归中序算法
2.2.3 脑对脑带您分析非递归中序代码
while(栈不为空||当前栈空但有右孩子未访问进栈)
{
每个结点根据LDR循环访问
while(当前根结点存在左(右)孩子){
(1)左(右)孩子遍历进栈
}
(2)栈顶结点直接出栈
(3)PNode保存当前栈顶结点以便后续执行(4)操作
(4)通过PNode访问栈顶结点右孩子,若右孩子存在则进栈
if(右孩子存在){
执行(1)操作,右孩子遍历进栈
}
}
2.3 后序遍历
2.3.1 后序遍历非递归代码实现
//后序非递归1
void EndOrder2(BTreeNode *b)
{
SqStack *s; //创建虚拟栈
StackInit(&s);
BTreeNode *TopNode; //用于读取栈顶元素结点
BTreeNode *PNode; //用于读取目标操作结点
BTreeNode *VisitedNode=NULL; //用于保存已访问结点
if(b!=NULL){
PNode=b;
while(PNode!=NULL||s->top>-1){
//(1)左孩子遍历进栈
while(PNode!=NULL){
/*
s->top++;
s->ST[s->top]=PNode;
*/
Push(&s,&PNode);
PNode=PNode->lchild;
}
//取栈顶
TopNode=s->ST[s->top]; //此处不能用GetTop因为top未变
//(2)栈顶元素若无右孩子或其右孩子已访问则可直接出栈
if(TopNode->rchild==NULL||VisitedNode==TopNode->rchild){
/*
printf("%c",TopNode->data);
s->top--;
*/
printf("%c",GetTop(&s,&TopNode)->data);
VisitedNode=TopNode; //标记为已访问 便于下一轮D->rchild的判断
PNode=NULL; //无右孩子进栈PNode置空跳过while循环
}
//(3)否则访问右孩子 到while循环进栈
else{
PNode=TopNode->rchild;
}
}
}
printf("\n");
StackDestory(&s);
}
2.3.2 手把手带您分析非递归后序算法
2.3.3 脑对脑带您分析非递归后序代码
while(栈不为空||栈空但仍有右孩子未进栈)
{
每个结点根据LRD循环访问
while(当前根结点存在左(右)孩子 ){
(1)左(右)孩子遍历进栈
}
(2)TopNode指向栈顶元素(注意此处top未变)
(3)栈顶元素若无右孩子或其右孩子已访问则可直接出栈
if(栈顶元素若无右孩子||栈顶元素右孩子已访问){
栈顶元素直接出栈
将出栈结点标记为已访问结点
}
(4)否则访问右孩子 到while循环进栈
else{
执行(1)步骤操作,右孩子进栈
}
}
2.4 简易后序遍历
2.4.1 原理
LRD可看成DRL的倒序,故我们可将结点按DLR遍历顺序先存入Traverse[MaxSize]数组 ,最后将数组元素倒序打印。
2.4.2 算法分析
由此上述分析可知,我们对前序非递归遍历做出两处修改即可实现后序遍历
(1)LRD->DRL->DLR
根据栈先进后出的原理,在DLR我们应先访问进栈右孩子再进栈左孩子,但访问左右孩子具体操作代码实现与先序遍历完全一致,故我们只需要将访问左右孩子的两端代码交换顺序即可。
(2)输出->存储
在先序遍历时,各结点按DLR顺序进栈,每轮循环通过GetTop取栈顶元素问打印。会发现,与前序遍历不同,此时我们不需要打印,我们只需要将原来打印的元素存储起来,其余操作代码实现完全一致。
故我们可定义一个数组,去存储我们原来每轮循环需要打印结点,循环结束,该数组内元素便是按照DRL顺序进行存储,还原成LRD的顺序,我们只需要将此数组倒序输出即可。
2.4.3 代码实现
//后序非递归2 倒序输出法
void EndOrder3(BTreeNode *b)
{
SqStack *s; //创建虚拟栈
StackInit(&s);
BTreeNode *TopNode; //用于读取栈顶元素结点
BTreeNode *PNode; //用于读取目标操作结点
BTreeNode *Traverse[MaxSize]; //临时按顺序存储结点
int index=0 ; //用于记录Traverse数组下标
int i; //用于倒序输出
if(b!=NULL){
//(1)根结点进栈
Push(&s,&b);
//栈不为空循环进行
while(s->top>-1){
//(2)取栈顶元素(D结点)
Traverse[index++] =GetTop(&s,&TopNode);
//因栈是先入后出 故DRl需先Push左子树再Push右子树
//(3)通过TopNode处理左子树 Push
if(TopNode->lchild!=NULL){
PNode=TopNode->lchild;
Push(&s,&PNode);
}
//(4)通过TopNode处理右子树 Push
if(TopNode->rchild!=NULL){
PNode=TopNode->rchild;
Push(&s,&PNode);
}
}
}
//倒序输出
for(i=index-1;i>=0;i--) {
printf("%c",Traverse[i]->data);
}
printf("\n");
StackDestory(&s);
}
附录 (完整代码实现)
#include