Harris角点特征提取和角点特征匹配（1）

Harris角点特征提取和特征匹配（前半部分）

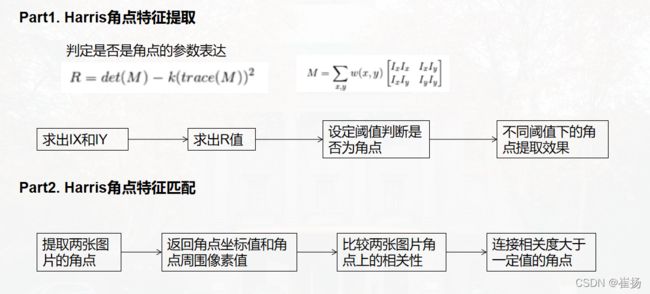
本文采用Harris角点的方法来进行特征提取和特征匹配两大部分：
1.Harris角点特征提取：分为函数法和机理法（手工复现法）
2.Harris角点特征匹配：先让两张图片进行特征提取，再将图一和图二的每一个点进行做相关运算，若两张图角点的相关度都是最大的，则将两张图的角点相匹配。

提示：以下程序是顺序的，要一一复制进行运行，目录需要自己更改，部分参数针对不同的图片，也要做出相应的改变

---

Part1. Harris角点特征提取

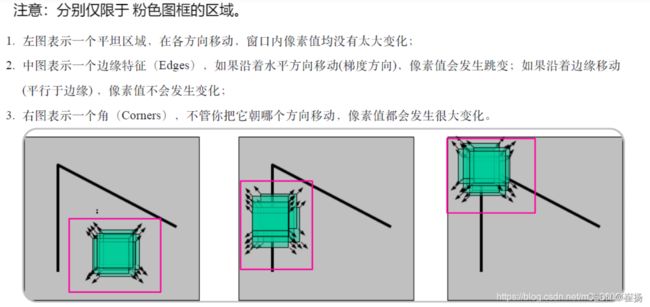
Harris角点特征提取基本思想是使用一个固定窗口在图像上进行任意方向上的滑动，比较滑动前与滑动后两种情况，窗口中的像素灰度变化程度，如果存在任意方向上的滑动，都有着较大灰度变化，那么我们可以认为该窗口中存在角点。下面这个图，赶紧很形象的说明了角点提取的机制：

一、函数法

1.利用OPEN-CV函数库的函数（也可以用PCV，不过此库版本较老没有使用）
cv2.cornerHarris(img,blocksize,ksize,k)

a. img 一般时二维的灰度图，float32的输入图像。

b. blocksize 角点检测中的窗口大小

c. ksize sobel算子的大小

d. 取值一般在[0.04,0.06]之间，而其时响应函数R中的一个参数。

import numpy as np
import cv2
import math
from numpy import *
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from PIL import Image

# 拿一张示例图可以看出测得出角点
img_block=cv2.imread('D:/classofmathpicture/house2.png',0)
img_block_C=cv2.cvtColor(img_block,cv2.COLOR_GRAY2RGB)
Harris_block = cv2.cornerHarris(img_block, 2, 3, 0.04)
dst = cv2.dilate(Harris_block, None)   #使检测角点变粗（红色角点更加明显）
thres = 0.1*dst.max()  # 把阈值设置到这么大都会检测出角点，说明函数法比较精确
img_block_C[dst > thres] = [255,0,0]
plt.imshow(img_block_C);plt.axis('off');

# 任何在采用一张图片来试验，其中阈值不同的情况下，特征提取的点数是不同的。
img_house=cv2.imread('D:/classofmathpicture/house1.png',0)
img_house_C=cv2.imread('D:/classofmathpicture/house1.png',1)
img_house_C=cv2.cvtColor(img_house_C,cv2.COLOR_BGR2RGB)
# img_house_C_fuction=img_house_C.copy()
Harris_house = cv2.cornerHarris(img_house, 3, 3, 0.04)
dst = cv2.dilate(Harris_house, None)  #将可以标出来的点粗化
plt.figure(figsize=(30, 20));
for i in range(9):
    img_house_C_fuction=img_house_C.copy()
    thres = 0.005*dst.max()*(5*i+1)
    img_house_C_fuction[dst > thres] = [255,0,0]
    plt.subplot(3,3,i+1);plt.imshow(img_house_C_fuction);
    plt.title('thres= %1.3f'%(0.005*(5*i+1)));plt.axis('off');

峰值的0.005倍-0.2倍作为阈值的比较图：

二、机理法

我将它分为三步，第一步求出Ix和Iy，同时窗函数乘上高斯窗，也可以用sobel()进行梯度提取；第二步求出R，第三步根据Ix、Iy、R与边角、边缘和平台区域的关系来构建阈值范围；第四步是衡量不同阈值下的角点提取效果。

第一步：求出IX和IY.

机理法对应函数法：cv2.cornerHarris(img,blocksize,ksize,k)，其中的参数可以得以更好的理解。blocksize就是划窗的范围，也就是划一次检测的窗口是多少，对应的也就是下面的c参数；

#计算x方向的梯度的函数（Ix）
def grad_x(h):
    delta_h = np.matrix(h)
    a = int(h.shape[0])
    b = int(h.shape[1])
    for i in range(a):
        for j in range(b):
            if i-1>=0 and i+1<a and j-1>=0 and j+1<b:
                 #注意像素不能直接计算，需要转化为整型 
                c=abs(int(h[i-1,j-1])-int(h[i+1,j-1]) + 2*(int(h[i-1,j]) -int(h[i+1,j])) + int(h[i-1,j+1]) - int(h[i+1,j+1]))   
                if c>255:
                    c = 255
                delta_h[i,j] = c
            else:
                delta_h[i,j] = 0
    return delta_h
##计算y方向的梯度的函数（Ix）
def grad_y(h):
    delta_h = np.matrix(h)
    a = int(h.shape[0])
    b = int(h.shape[1])
    for i in range(a):
        for j in range(b):
            if i-1>=0 and i+1<a and j-1>=0 and j+1<b:
                c = abs(int(h[i-1,j-1]) - int(h[i-1,j+1]) + 2*(int(h[i,j-1]) - int(h[i,j+1])) + (int(h[i+1,j-1]) - int(h[i+1,j+1]))) 
                if c > 255:
                    c = 255
                delta_h[i,j] = c
            else:
                delta_h[i,j] = 0
    return delta_h

第二步：求出R

ksize就是sobel的算子，也就是高斯函数中的A1,B1,C1表达式中的（3，3）；k是评判阈值R的表达式中的参数k，机理法表达式写成：

R[i,j] = np.linalg.det(M) - k * (np.trace(M)) * (np.trace(M))

def harris_manual(img_house):
    dx = np.array(grad_x(img_house))
    dy = np.array(grad_y(img_house))
    A = dx * dx
    B = dy * dy 
    C = dx * dy
    A1 = cv2.GaussianBlur(A,(3,3),1.5)    #sobel算子取3
    B1 = cv2.GaussianBlur(B,(3,3),1.5)  
    C1 = cv2.GaussianBlur(C,(3,3),1.5)
    a = int(img_house.shape[0])
    b = int(img_house.shape[1])
    R = np.zeros(img_house.shape)
    for i in range(a):
        for j in range(b):
            M = [[A1[i,j],C1[i,j]],[C1[i,j],B1[i,j]]]   #窗函数是2*2的矩形窗
            R[i,j] = np.linalg.det(M) - 0.04 * (np.trace(M)) * (np.trace(M))  #k取0.04，与函数法保持一致
    return R

第三步，根据对应关系来设定阈值

. 特征值都比较大时，即窗口中含有角点

. 特征值一个较大，一个较小，窗口中含有边缘

. 特征值都比较小，窗口处在平坦区域

程序一是拿方块图做实验，设定了四种情况，第一种R、Ix、Iy三个特征值都较大，画出角点；第二种是Ix远大于Iy，画出横向的边缘；第三种画出竖向的边缘；第四周是三个特征值都较小，画出平坦区域。结果得以验证上面的机理法是正确的

# 程序一：方块
img_block_C=cv2.imread('D:/classofmathpicture/house2.png',1)
img_block_C=cv2.cvtColor(img_block_C,cv2.COLOR_BGR2RGB)
img_block=cv2.imread('D:/classofmathpicture/house2.png',0)
R_block=harris_manual(img_block)
img_block_C_manual_edge_h=img_block_C.copy()
img_block_C_manual_edge_l=img_block_C.copy()
img_block_C_manual_flat=img_block_C.copy()
img_block_C_manual_corner=img_block_C.copy()
dx_block = np.array(grad_x(img_block))
dy_block = np.array(grad_y(img_block))
thres = 0.1*R_block.max()
dxres = 0.1*dx_block.max()
dyres = 0.1*dy_block.max()
a = int(img_block.shape[0])
b = int(img_block.shape[1])
for i in range(a):
    for j in range(b):
        if (abs(R_block[i,j]) > thres) and (dx_block[i,j]>dxres) and (dy_block[i,j]>dyres):
            img_block_C_manual_corner[i,j,:] = [255,0,0]
        if (R_block[i,j]<0) and (int(dx_block[i,j])-int(dy_block[i,j]))>4*dxres:
            img_block_C_manual_edge_h[i,j,:] = [255,0,0]
        if (R_block[i,j]<0) and (int(dy_block[i,j])-int(dx_block[i,j]))>4*dxres:
            img_block_C_manual_edge_l[i,j,:] = [255,0,0]
        if abs(R_block[i,j]) <0.5*thres and (dx_block[i,j]<0.5*dxres) and (dy_block[i,j]<0.5*dyres):
            img_block_C_manual_flat[i,j,:] = [255,0,0]
plt.figure(figsize=(30, 20));
plt.subplot(221);plt.imshow(img_block_C_manual_corner);plt.title('manual_way_corner');plt.axis('off');
plt.subplot(222);plt.imshow(img_block_C_manual_edge_h);plt.title('manual_way_edge_h');plt.axis('off');
plt.subplot(223);plt.imshow(img_block_C_manual_edge_l);plt.title('manual_way_edge_l');plt.axis('off');
plt.subplot(224);plt.imshow(img_block_C_manual_flat);plt.title('manual_way_flat');plt.axis('off');

下图分别为角点提取，x梯度提取，y梯度提取和平坦区域提取：

# 程序二：房子，把上面程序中的图片换成房子即可

第四步：衡量不同阈值下的角点提取效果

和函数法同理，采取了R最大值的不同系数来作为阈值：0.005*(5*x+1)*R_house.max()
在采取相同系数效果下，效果与函数法大有不同（可能是函数法的阈值系数与机理法的意思不同），但是总体能得出系数等于0.2最为合适

若想看后半部分-Harris角点特征匹配，点击链接：
https://blog.csdn.net/QWER306306/article/details/123830827