BN（Batch Normalization）：批量归一化

现在的神经网络通常都特别深，在输出层像输入层传播导数的过程中，梯度很容易被激活函数或是权重以指数级的规模缩小或放大，从而产生“梯度消失”或“梯度爆炸”的现象，造成训练速度下降和效果不理想。

随着训练的进行，网络中的参数也随着梯度下降在不停更新，一方面，当底层网络中参数发生微弱变化时，由于每一层中的线性变换与非线性激活映射，这些微弱变化随着网络层数的加深而被放大；另一方面，参数的变化导致每一层的输入分布会发生改变，进而上层的网络需要不停的去适应这些分布变化，使得模型训练变得困难。这种现象叫Internal Covariate Shift。

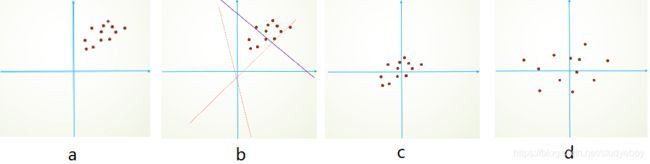
Internal Covariate Shift是BN论文作者提出来的概念，表示呼叫的分布在网络传播的过程中会发生偏移，举例解释，假设有一个玫瑰花的深度学习网络，这是一个二分类的网络，1表示识别为玫瑰花，0则表示非玫瑰花。先看训练数据集的一部分，直观来说，玫瑰花的特征表现很明显，都是红色玫瑰花。

再看训练数据集的另一部分，很明显，这部分数据的玫瑰花各种颜色都有，其特征分布与上述数据集是不一样的。

通俗的讲，刚开始的数据都是同一个分布的，模型学习过程中，模型的参数已经适合于一种分布，突然又要适应另一种分布，这就会让模型的参数发生很大的调整，从而影响到收敛的速度和精度。这就是Internal Covariate Shift。

BN的作用就是将这些输入值或卷积网络的张量进行列数标准化操作，将其放缩到合适的范围，从而加快训练速度；另一方面使得每一层可以尽量面对同一特征分布的输入值，减少了变化带来的不确定性。

网络训练起来，那么参数就要更新，除了输入层的数据外（因为输入层数据，已经人为的为每个样本归一化），后面网络每一层的输入数据分布是一直在发生变化的，因为在训练的时候，前面层训练参数的更新将导致后面层输入数据分布的变化。以网络第二层为例：网络的第二层输入，是由第一层的参数和input计算得到的，而第一层的参数在整个训练过程中一直在变化，因此必然会引起后面每一层输入数据分布的改变。我们把网络中间层在训练过程中，数据分布的改变称之为“Internal Covariate Shift”。BN的提出，就是要解决在训练过程中，中间层数据分布发生改变的情况。

Internal Covariate Shift带来的问题：

• 上层网络需要不停调整来适应输入数据分布的变化，导致网络学习速度的降低。
• 网络的训练过程容易陷入梯度饱和区，减缓网络收敛速度。

网络训练过程中参数不断改变导致后续每一层输入的分布也发生变化，而学习的过程又要使每一层适应输入的分布。

为了减缓Internal Covariate Shift的方法，出现了白化法，对输入数据分布进行变换，使得输入特征分布具有相同的均值和方差，去除特征之间的相关性。

为什么减均值、白化可以加快训练？

• 首先，图像数据是高度先关的，假设其分布如下图a所示（简化为2维）。由于初始化的时候，我们的参数一般都是0均值，因此，开始的拟合y=Wx+b，基本过原点附近，如图b红色虚线。因此，网络需要经过多次学习才能逐步达到如紫色实线的拟合，即收敛的比较慢。如果我们对输入数据先做减均值操作，如图c，显然可以加快学习。更进一步，我们对数据再进行去相关操作，使得数据更加容易区分，这样又会加快训练，如图d。
  

白化（whiting）是机器学习里面常用的一种规范化数据分布的方法，主要是PCA白化与ZCA白化。

白化的缺点：

• 白化过程计算成本太高，并且在每一轮训练中的每一层我们都需要做如此高成本计算的白化操作。例如PCA白化：即对数据进行PCA操作之后，再进行方差归一化，这样数据基本满足0均值、单位方差、弱相关性。对每一层数据都使用白化操作，因为白化需要计算协方差矩阵、求逆等操作，计算量很大，此外，反向传播时，白化操作不一定可导。
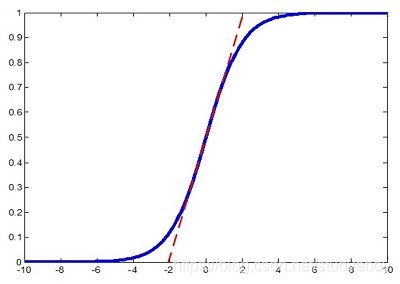
• 白化过程由于改变了网络每一层的分布，因而改变了网络层中本身数据的表达能力。底层网络学习到的参数信息会被白化操作丢失掉。比如下图所示，在使用sigmoid激活函数的时候，如果把数据限制到0均值、单位方差，那么相当于只使用了激活函数中近似线性的部分，这显然会降低模型表达能力。
  

为了能够简化计算过程，又需要经过规范化处理后让数据尽可能保留原始的表达能力。提出了简化+改进版的白化——Batch Normalization。

既然白化计算过程比较复杂，尝试单独对每个特征进行normalization，让每个特征都有均值为0，方差为1的分布。既然白化操作减弱了网络中每一层输入数据表达能力，就再加个线性变换操作，让这些数据再能够尽可能恢复本身的表达能力。

BN 是由Google于2015年提出，论文是《Batch Normalization Accelerating Deep Network Training by Reducing Internal Covariate Shift》，这是一个深度神经网络训练的技巧，它不仅可以加快模型的收敛速度，而且在一定程度缓解了深层网络中“梯度弥散”的问题，从而使得训练深层网络模型更加容易和稳定。

Batch Normalization是对每一批数据进行归一化，以前的归一化操作都在数据输入层，对输入的数据进行求均值以及求方差做归一化，但是BN可以在网络中任意一层进行归一化处理，因为现在所有的优化方法大多都是基于mini-batch 进行的随机梯度优化算法，所以归一化操作也是基于mini-batch的。
某一批次的张量通过卷积层并加上偏置后，ReLU激活之前，即。

• 求每一个训练批次数据的均值
• 求每一个训练批次数据的方差
• 使用求得的均值和方差对该批次的训练数据做归一化，获得0-1分布，其中$ϵ$是为了避免除数为0时所使用的微小整数。
• 尺度变换和偏移：将$x_i$乘以$\gamma$调整数值大小，再加上$\beta$增加偏移后得到$y_i$，这里的$\gamma$是尺度因子，$\beta$是平移因子。这一步是BN的精髓，由于归一化后的$x_i$基本会被限制在正态分布下，使得网络的表达能力下降。为了解决该问题，引入两个新的参数$\gamma$和$\beta$，它们是在训练时网络自己学习得到的。

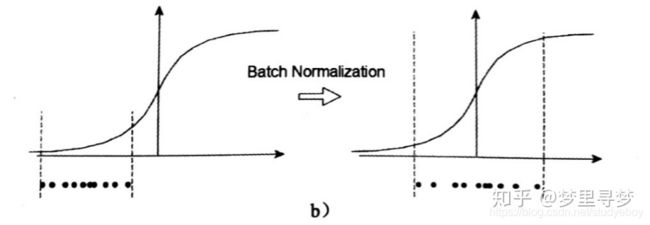
a中昨天是没有经过任何处理的输入数据，曲线是sigmoid函数，如果数据在梯度很小的区域，那么学习率就会很慢，甚至陷入长时间的停滞。减均值除方差后，数据就被移动到中心区域如右图所示，对于大多数激活函数而言，这个区域的梯度都是最大的或者是有梯度的（比如ReLU），这可以看作是一种对抗梯度消失的有效手段。对于一层如此，如果对于每一层数据都那么做的话，数据的分布总是在随着变化敏感的区域，相当于不用考虑数据分布变化了，这样训练起来更有效率。

但是仅减均值除方差得到的正太分布并不可能就是最好或最能体现训练样本的特征分布。比如数据本身很不对称，或者激活函数未必是对方差为1的数据最好的效果，比如sigmoid激活函数，在-1~1之间的梯度变化不大，那么非线性变换的作用就不能很好的体现，即减均值除方差操作后可能会削弱网络的性能，针对该情况，在前面三步之后加入第4步完成真正的batch normalization。

BN的本质就是利用优化变一下方差大小和均值位置，使得新的分布更切合数据的真实分布，保证模型的非线性表达能力。BN的极端情况就是这两个参数等于mini-batch的均值和方差，那么经过batch normalization之后的数据和输入完全一样，当然一般情况下是不同的。

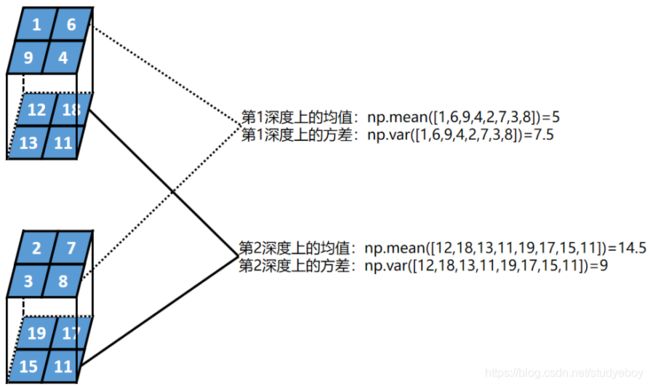
假设某一批次的数据为2个2行2列深度的张量，BN的过程如下：

• 计算每一层深度的均值和方差
  

• 对每一层设置2个参数，$\gamma$和$\beta$。假设第1深度$\gamma =2,\beta =3$，第2深度$\gamma =2,\beta =3$。计算公式：
  
  

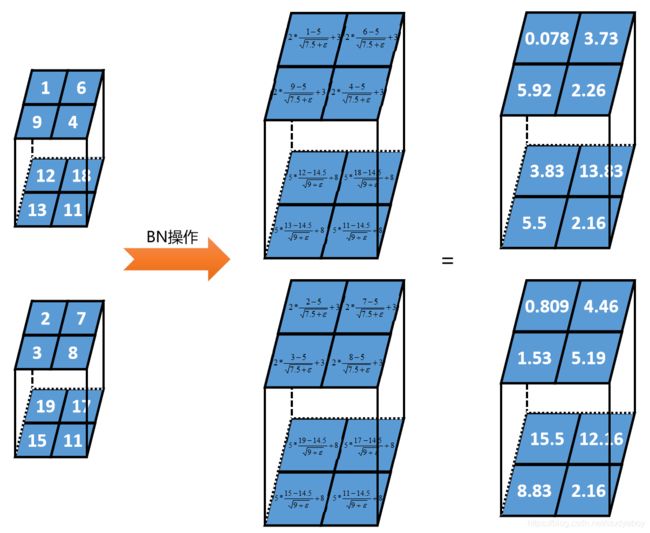
上面的都是训练时的BN算法，训练时是一个一个batch输入的，训练完成后得到$\gamma$和$\beta$。但是在测试时，只是丢一个样本进去让网络预测，均值和方差最好的来源是整个训练集，但是整个训练集往往太大。可以从现成的mini-batch的均值和方差（因为在训练时算子出来）估计出整个训练集的均值和方差，因为mini-batch是随机取样的：

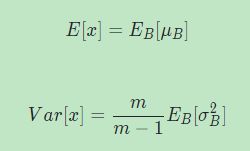
即平均值为所有mini-batch的平均值的平均值，而方差为每个batch的方差的无偏估计。当网络训练完后，我们通过训练时保存下来的每个batch的均值与方差估算出全局均值与方差供测试时使用，也就是说当网络训练完后每个NB层中的均值和方差也会随之确定。

BN优点：

• BN是得网络中每层输入数据的分布相对稳定，加速模型学习速度。
  BN通过规范化与线性变换使得每一层网络的输入数据的均值与方差都在一定范围内，使得后一层网络不必不断取适应底层网络中输入的变化，从而实现了网络中层与层之间的解耦，允许每一层进行独立学习，有利于提高整个神经网络的学习速度。
• BN使得模型对网络中的参数不那么敏感，简化调参过程，使得网络学习更加稳定。
  在神经网络中，经常会谨慎的采用一些权重初始化方法（例如Xavier）或者合适的学习率俩保证网络稳定训练。
• BN允许网络使用饱和性激活函数（例如sigmoid，tanh等），缓解梯度消失问题。
  在不使用BN层的时候，由于网络的深度与复杂性，很容易使得底层网络变化累积到上层网络中，导致模型的训练很容易进入到激活函数的梯度饱和区；通过normalize操作可以让激活函数的输入数据在梯度非饱和区，缓解梯度消失的问题；另外通过自适应学习$\gamma$与$\beta$又让数据保留更多的原始信息。
• BN具有一定的正则化效果。
  在Batch Normalization中，由于我们使用mini-batch的均值与方差作为对整体训练样本均值与方差的估计，尽管每一个batch中的数据都是从整体样本中抽样得到的，但不同mini-batch的均值与方差会有所不同，这就为网络的学习过程中增加了随机噪声，与Dropout通过关闭神经元给网络训练带来噪音类似，在一定程度上对模型起到了正则化的效果。另外，原作者也证明了网络加入BN后，可以丢弃Dropout，模型同样具有很好的泛化效果。

BN缺点：

• 如果Batch size太小，则BN效果明显下降。
  BN是严重依赖mini-batch中的训练实例，如果batch size 比较小则任务效果有明显的下降。下图给出了在ImageNet数据集下做分类任务时，使用ResNet的时候模型性能随着batch size变化时的性能变化情况，可以看出当batch size小于8的时候开始对分类效果有明显负面影响。因为在小的batch size意味着数据样本少，因而得不到有效统计量，也就是说噪声太大。
  

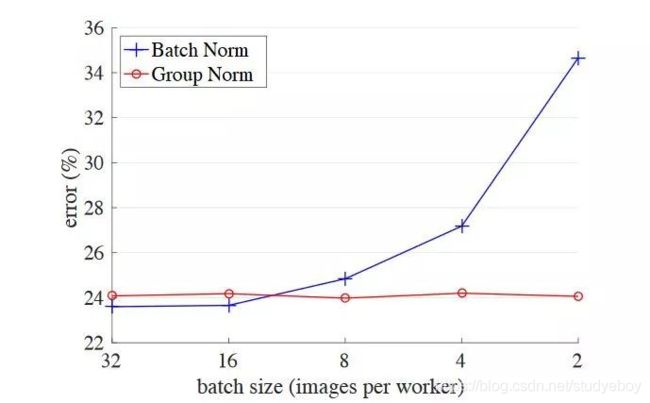
• 对于有些像素级图片生成任务来说，BN效果不佳。
  对于图像分类等任务，只要能够找出关键特征，就能正确分类，这算是一种粗粒度的任务，在这种情形下通常BN是有积极效果的。但是对于有些输入输出都是图片的像素级别图片生成任务，比如图片风格转换等应用场景，使用BN会带来负面效果，这很可能是因为在mini-batch内多张无关的图片之间计算统计量，弱化了单张图片本身特有的一些细节信息。

• RNN等动态网络使用BN效果不佳且使用起来不方便。
  对于RNN来说，尽管其结构看上去是个静态网络，但在实际运行展开时是个动态网络结构，因为输入的Sequence序列是不定长的，这源自同一个Mini-Batch中的训练实例有长有短。对于类似RNN这种动态网络结构，BN使用起来不方便，因为要应用BN，那么RNN的每个时间步需要维护各自的统计量，而Mini-Batch中的训练实例长短不一，这意味着RNN不同时间步的隐层会看到不同数量的输入数据，而这会给BN的正确使用带来问题。假设Mini-Batch中只有个别特别长的例子，那么对较深时间步深度的RNN网络隐层来说，其统计量不方便统计而且其统计有效性也非常值得怀疑。另外，如果在推理阶段遇到长度特别长的例子，也许根本在训练阶段都无法获得深层网络的统计量。综上，在RNN这种动态网络中使用BN很不方便，而且很多改进版本的BN应用在RNN效果也一般。

• 训练时和推理时统计量不一致。
  对于BN来说，采用Mini-Batch内实例来计算统计量，这在训练时没有问题，但是在模型训练好之后，在线推理的时候会有麻烦。因为在线推理或预测的时候，是单实例的，不存在Mini-Batch，所以就无法获得BN计算所需的均值和方差，一般解决方法是采用训练时刻记录的各个Mini-Batch的统计量的数学期望，以此来推算全局的均值和方差，在线推理时采用这样推导出的统计量。虽说实际使用并没大问题，但是确实存在训练和推理时刻统计量计算方法不一致的问题。

参考资料
（BN）批量归一化全面解析
批量归一化（BN, Batch Normalization）
Batch Normalization（BN，批量归一化）
深度学习面试题21：批量归一化(Batch Normalization,BN)
【DL-CV】批量归一化（BN算法）
来聊聊批归一化BN（Batch Normalization）层
深度学习：批归一化和层归一化Batch Normalization、Layer Normalization