python使用反向传播（backpropagation）算法在sklearn库自带的缩小版MINIST手写数据集（1797张图片）上进行训练并测试

python代码实现

神经网络的构建，NeuralNetwork.py

import numpy as np


# layers:  A list of integers which represents the actual architecture of the feedforward
# network. For example, a value of [2,2,1] would imply that our first input layer has two nodes,
# our hidden layer has two nodes, and our final output layer has one node.

# alpha:这里我们可以指定神经网络的学习率。此值在权重更新阶段应用。


class NeuralNetwork:
    def __init__(self, layers, alpha=0.1):
        self.W = []
        self.layers = layers
        self.alpha = alpha

        # 初始化权重矩阵
        for i in np.arange(0, len(layers) - 2):
            w = np.random.randn(layers[i] + 1, layers[i + 1] + 1)
            self.W.append(w / np.sqrt(layers[i]))

            # 上述for代码解释：例如，假设layers[i] = 2, layers[i + 1] = 2。因此，我们的权值矩阵将是2x2，以连接各层之间的所有节点集。然而，在这里我们需要小心，因为我们忘记了一个重要的组成部分——偏见项。为了解释这种偏差，我们在层数[i]和层数[i + 1]上加1——这样做会改变我们的权值矩阵w，使形状3x3给定当前层的2 + 1个节点和下一层的2 + 1个节点。我们通过除以当前层中节点数量的平方根来缩放w，从而标准化每个神经元输出[57]的方差(第19行)。

        # 构造函数中需要处理的特殊情况，其中输入连接需要一个偏置项，但输出不需要
        w = np.random.randn(layers[-2] + 1, layers[-1])
        self.W.append(w / np.sqrt(layers[-2]))


    # 定义的一个对函数调试有用处的函数，主要是得到当前网络的架构层数，以及每一层的节点数
    def __repr__(self):
        # construct  and  return  a  string  that  represents  the  network

        # architecture
        return "NeuralNetwork:  {}".format("-".join(str(l) for l in self.layers))

    # 定义sigmoid激活函数
    def sigmoid(self, x):
        return 1.0 / (1 + np.exp(-x))


    # 同时我们将在反向传播过程中用到上述sigmoid函数的导数
    def sigmoid_deriv(self, x):
        return x * (1 - x)

    # 需要注意的是无论何时需要适用反向传播函数，再次注意，无论何时执行反向传播，您都希望选择一个可微的激活函数。

    # 定义一个fit函数来训练我们的神经网络
    def fit(self, X, y, epochs=1000, displayUpdate=100):
        X = np.c_[X, np.ones((X.shape[0]))]

        for epoch in np.arange(0, epochs):
            for (x, target) in zip(X, y):
                self.fit_partial(x, target)

            if epoch == 0 or (epoch + 1) % displayUpdate == 0:
                loss = self.calculate_loss(X, y)
                print("[INFO] epoch={}, loss={:.7f}".format(epoch + 1, loss))


    # 反向传播函数的核心在下面的函数中
    def fit_partial(self, x, y):
        # 初始化一个保存每层输出的网络
        A = [np.atleast_2d(x)]


        # 开始向前传播
        for layer in np.arange(0, len(self.W)):
            # 得到每层网络的权值和网络层的数据点之间的乘积
            net = A[layer].dot(self.W[layer])

            # 通过激活函数得到每层网络的输出
            out = self.sigmoid(net)

            # 将输出追加到A中
            A.append(out)

            # We start looping over every layer in the network on Line 71. The net input to the current layer
            # is computed by taking the dot product between the activation and the weight matrix (Line 76). The
            # net output of the current layer is then computed by passing the net input through the nonlinear
            # sigmoid activation function. Once we have the net output, we add it to our list of activations (Line
            # 84).

        # 进行反向传播
        error = A[-1] - y

        # 从这里开始，我们需要应用链式法则并构建我们的94 # delta ' D '列表;delta中的第一个条目是95 #，即输出层的误差乘以激活函数对输出值的导数96 #

        D = [error * self.sigmoid_deriv(A[-1])]

        # 向后传递的第一阶段是计算我们的错误，或者简单地计算我们的预测标签和地面真相标签之间的差值(第91行)。由于激活列表A中的最后一个条目包含了网络的输出，我们可以通过A[-1]访问输出预测。值y是输入数据点x的目标输出。

        #接下来，我们需要开始应用链式法则来构建delta的列表d。delta将被用来更新我们的权值矩阵，按学习速率缩放。delta列表中的第一个条目是输出层的误差乘以输出值的sigmoid的导数(第97行)。

        for layer in np.arange(len(A) - 2, 0, -1):
            delta = D[-1].dot(self.W[layer].T)
            delta = delta * self.sigmoid_deriv(A[layer])
            D.append(delta)

            # 在第103行，我们开始对网络中的每一层进行循环(忽略前面的两层，因为它们已经在第97行中被计入了)，因为我们需要反向计算每一层的增量更新。当前层的delta等于前一层的delta，用当前层的权值矩阵点乘D[-1](第109行)。为了完成delta的计算，我们通过将层的激活通过我们的s形函数的导数(第110行)来乘以它。然后，我们用刚刚计算的增量更新增量D列表(第111行)。

            # 看看这段代码，我们可以看到反向传播步骤是迭代的——我们只是从上一层取delta，用当前层的权值点乘它，然后乘以激活的导数。这个过程不断重复，直到我们到达网络的第一层。

        # 翻转D矩阵
        D = D[::-1]

        for layer in np.arange(0, len(self.W)):
            self.W[layer] += -self.alpha * A[layer].T.dot(D[layer])


    # 定义预测函数
    def predict(self, X, addBias=True):
        p = np.atleast_2d(X)
        if addBias:
            p = np.c_[p, np.ones((p.shape[0]))]

        for layer in np.arange(0, len(self.W)):
            p = self.sigmoid(np.dot(p, self.W[layer]))
        return p

    # 定义的一个计算训练集中损失的函数
    def calculate_loss(self, X, targets):
        targets = np.atleast_2d(targets)
        predictions = self.predict(X, addBias=False)
        loss = 0.5 * np.sum((predictions - targets) ** 2)

        return loss

在MINIST手写数据集上进行训练并测试，nn_mist.py

from pyimagesearch.nn import NeuralNetwork
from sklearn.preprocessing import LabelBinarizer
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
from sklearn import datasets


# 开始训练MINIST数据集
print("[INFO]  loading  MNIST  (sample)  dataset...")
digits = datasets.load_digits()
data = digits.data.astype("float") # 将数据集转换为float类型
data = (data - data.min()) / (data.max() - data.min())  # 作归一化处理
print("[INFO]  samples:  {},  dim:  {}".format(data.shape[0], data.shape[1]))

# 将数据集进行分分类，75%作为训练集，25%作为测试集
(trainX,  testX,  trainY,  testY)  =  train_test_split(data, digits.target,  test_size=0.25)

# 使用one-hot编码将对应的标签进行向量化
trainY  =  LabelBinarizer().fit_transform(trainY)
testY  =  LabelBinarizer().fit_transform(testY)


# 训练网络
print("[INFO]  training  network...")
nn  =  NeuralNetwork.NeuralNetwork([trainX.shape[1], 32, 16, 10]) # 初始化神经网络
print("[INFO]  {}".format(nn))
nn.fit(trainX,  trainY,  epochs=1000) # 对神经网络进行训练


# 测试网络，并标准化输出对应的一些指标
print("[INFO]  evaluating  network...")
predictions  =  nn.predict(testX)
predictions  =  predictions.argmax(axis=1)
print(classification_report(testY.argmax(axis=1),  predictions))

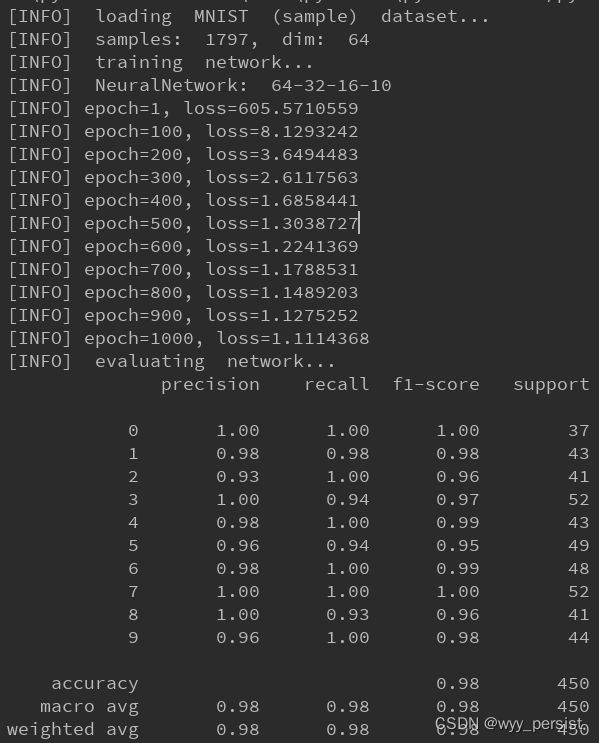
训练结果展示