【学习OpenCV4】图像变换方法总结（放缩、翻转、旋转）

一、图像放缩Resize

1.1 基本知识
  图像放缩用到了许多插值方法，常见的差值算法有线性插值、立方差值、双立方差值、采样放缩算法等等。
  所使用的API为 resize()，函数的定义如下

void resize(
InputArray src,	//输入图像
OutputArray dst,//输出图像
Size dsize,		//输出尺寸
double fx=0,	//水平缩放比例
double fy=0,	//垂直缩放比例
int interpolation=INTER_LINEAR	//插值方式
)

• 其中dsize为0时，fx和fy均不可为零；fx和fy为0时，输出图像按dsize输出
• interpolation内插方式有以下四种：
  • CV_INTER_NEAREST  最邻近插值点法
  • CV_INTER_LINEAR   双线性插值法
  • CV_INTER_AREA    邻域像素再取样插补
  • CV_INTER_CUBIC     双立方插补，4*4大小的补点

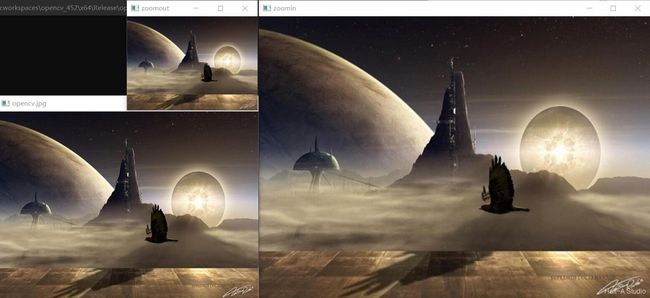
1.2 示例程序

void MyDemo::resize_Demo(Mat& image) {
	Mat zoomin, zoomout;	//定义输出图像
	int h = image.rows;		//获取原图像的宽高
	int w = image.cols;
	resize(image, zoomin, Size(w * 1.5, h * 1.5), 0, 0, INTER_LINEAR);	//图像放大1.5倍
	imshow("zoomin", zoomin);
	resize(image, zoomout, Size(w / 2, h / 2), 0, 0, INTER_LINEAR);		//图像缩小2倍
	imshow("zoomout", zoomout);
}

二、图像翻转flip

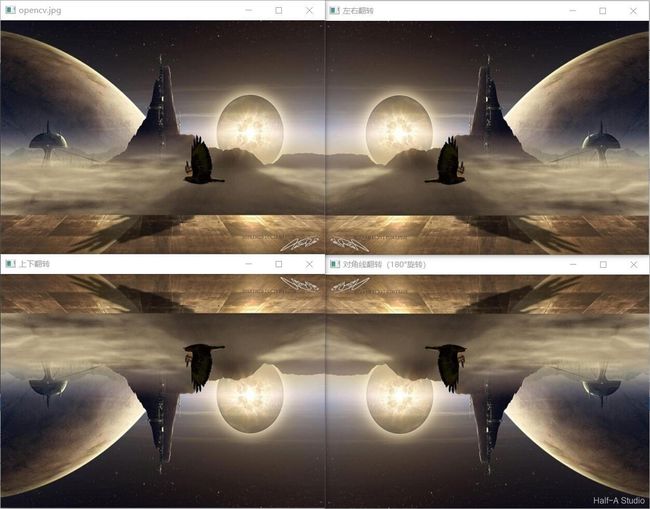
  图像反转就是将图像左右或上下反转镜像。所用到的函数是 flip()，函数的定义如下。

	void cv::flip(
		cv::InputArray 	src, 			// 输入图像
		cv::OutputArray dst, 			// 输出图像
		int 			flipCode = 0	// >0: 沿y轴翻转, 0: 沿x轴翻转, <0: x、y轴同时翻转
	);

测试程序如下：

void MyDemo::flip_Demo(Mat& image) {
	Mat dst;
	flip(image, dst, 0);	//上下翻转
	imshow("上下翻转", dst);
	flip(image, dst, 1);	//左右翻转
	imshow("左右翻转", dst);
	flip(image, dst, -1);	//对角线翻转（180°旋转）
	imshow("对角线翻转（180°旋转）", dst);
}

三、图像旋转warpAffine

void cv::warpAffine (
	InputArray 		src,	//输入图像
	OutputArray 	dst,	//输出图像
	InputArray 		M,		//变换矩阵
	Size			dsize,	//输出图像大小
	int				flags = INTER_LINEAR,			//插值方式
	int 			borderMode = BORDER_CONSTANT,	//图像边缘像素模式
	const Scalar&	borderValue = Scalar()			//边界填充值

其中M变换矩阵可以通过如下函数获得，旋转矩阵的形式如下：

M=cv2.getRotationMatrix2D(center, angle, scale)

由于旋转之后，图像的大小会发生变化，因此需要重新计算图像的长宽，计算方法可以参考下图：

图像旋转的示例程序如下：

void MyDemo::rotate_Demo(Mat& image) {
	Mat dst, M;
	int h = image.rows;
	int w = image.cols;
	M = getRotationMatrix2D(Point2f(w / 2, h / 2), 45, 1.0);	//定义变换矩阵M
	double cos = abs(M.at<double>(0, 0));	//求cos值
	double sin = abs(M.at<double>(0, 1));	//求sin值
	int nw = cos * w + sin * h;		//计算新的长、宽
	int nh = sin * w + cos * h;
	M.at<double>(0, 2) += (nw / 2 - w / 2);		//计算新的中心
	M.at<double>(1, 2) += (nh / 2 - h / 2);
	warpAffine(image, dst, M, Size(nw,nh), INTER_LINEAR,0,Scalar(255,255,255));
	imshow("Rotation", dst);
}