【入门教程】使用keras实现线性回归

【1】在此篇，我们将使用神经网络来解决线性回归问题，实际上是一个单输入单输出的神经网络模型，下面我将使用keras简单进行回归模型的预测。

导入模型所需要的包

import numpy as np
from keras.models import Sequential
from keras.layers import Dense
from keras import optimizers
import matplotlib.pyplot as plt

创建数据集，并构建模型

X = np.random.randint(0,100,(200,3))
a = [[5],[1.5],[1]]
Y = np.mat(X) * np.mat(a) + np.random.normal(0,0.05,(200,1))#假定函数关系为y=w[x]+b
#划分训练集和测试集合
X_train,y_train = X[:160],Y[:160]
X_test,y_test = X[160:],Y[160:]
#建立模型
model = Sequential()
model.add(Dense(output_dim=1, input_shape=(3,)))
model.compile(optimizers.Adam(lr=0.001,beta_2=0.999),loss="mse")
#训练模型
history = model.fit(X_train,y_train,epochs=3000)
cost = model.evaluate(X_test,y_test)
print(model.layers[0].get_weights())

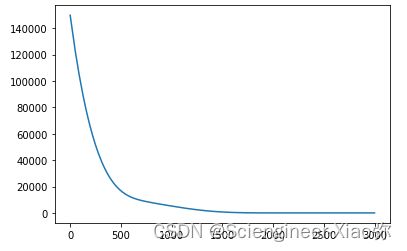
通过以上单层输入输出的模型结果可以看到模型的系数拟合的还是十分准确的。下图为训练epochs与损失的变化曲线。

plt.plot(range(3000),history.history["loss"])
plt.show()

【2】在这里，我们对高次线性回归进行曲线拟合。按照同样的流程：

导入相应的库

import numpy as np
import matplotlib.pyplot as plt
from keras.layers import Dense
from keras.models import Sequential
from keras.optimizers import SGD
from keras.layers import Activation

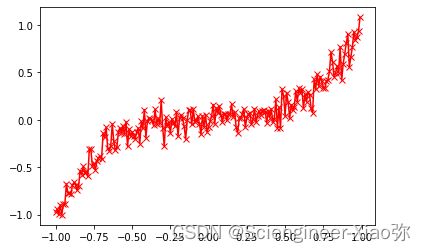
绘出散点图

X_train = np.arange(-1,1,0.01)
Y_train = X_train**3 + np.random.normal(0,0.1,200)
plt.plot(X_train,Y_train,c='r',marker="x")
plt.show()

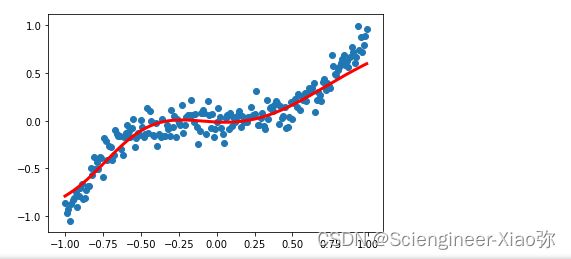
建立模型并预测结果

model = Sequential()
model.add(Dense(units=10, input_dim=1))
model.add(Activation('tanh'))
model.add(Dense(units=1))
model.add(Activation('tanh'))
model.summary()
sgd = SGD(lr=0.3)
model.compile(optimizer="adam", loss='mse')
history = model.fit(X_train,Y_train,epochs=2000,validation_split=0.2)
y_pred = model.predict(X_train)
plt.scatter(X_train, Y_train)
plt.plot(X_train, y_pred, 'r-', lw=3)
plt.show()