cs224w 图神经网络 学习笔记(十六)Network Evolution
课程链接:CS224W: Machine Learning with Graphs
课程视频:【课程】斯坦福 CS224W: 图机器学习 (2019 秋 | 英字)
目录
-
- 1. Evolving Networks
- 2. Macroscopic Evolution of Networks
-
- 2.1 网络中节点数量和边的数量随时间的变化
- 2.2 网络直径随时间的变化
- 2.3 网络度分布(degree distribution)随时间的变化
- 2.4 Forest fire model
- 3. Temporal Networks 含时网络/时序网络
- 4. Microscopic Evolution of Networks
-
- 4.1 Temporal path
- 4.2 Temporal PageRank
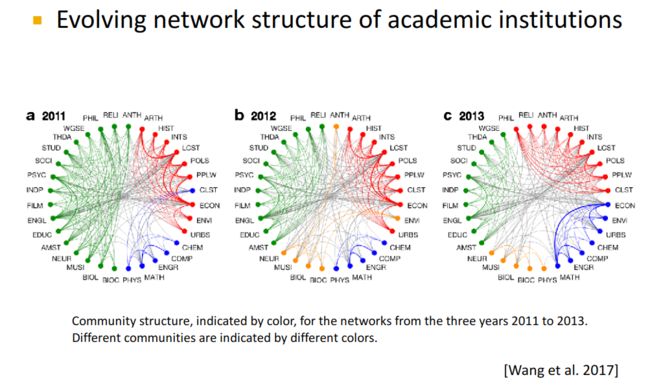
- 5. Mesoscopic Evolution of Networks
1. Evolving Networks
Evolving Networks——networks that change as a function of time 随着时间演化的网络(几乎所有现实世界的网络都是随着时间的推移而增加或删除节点或链接)
万物之间的联系总是会变得越来越紧密。例如人的社交网络,我们一开始其实社交圈子特别小,随着不断地交往,我们的社交圈子会不断扩大。
- macro level——Evolving network models, densification
- meso level——Network motifs, communities
- micro level——Node, link properties (degree, network centrality)
2. Macroscopic Evolution of Networks
从宏观的角度去看,我们主要考虑下面三个问题:
- 网络中节点数量和边的数量随时间的变化
- 网络直径随时间的变化
- 网络**度分布(degree distribution)**随时间的变化
2.1 网络中节点数量和边的数量随时间的变化
假设 t t t时刻节点的数量为 N ( t ) N(t) N(t),边的数量为 E ( t ) E(t) E(t),如果再 t + 1 t+1 t+1时刻,节点的数量变为了 2 ⋅ N ( t ) 2 \cdot N(t) 2⋅N(t),即 N ( t + 1 ) = 2 ⋅ N ( t ) N(t+1)=2 \cdot N(t) N(t+1)=2⋅N(t),那么边的数量该怎么变化呢?——并不是简单的翻倍,而是遵循Densification Power Law(密集幂分布率)。
E ( t ) ∝ N ( t ) α E(t) \propto N(t)^\alpha E(t)∝N(t)α
其中 α \alpha α为致密化指数(densification exponent), 1 ≤ α ≤ 2 1 \le \alpha \le 2 1≤α≤2。如果 α = 1 \alpha=1 α=1,则为线性增长,每个节点的出度都是一样的;如果 α = 2 \alpha=2 α=2,则为二次增长,即一个完全图。

上式等价于
log ( E ( t ) ) log ( N ( t ) ) = c o n s t \frac{\log (E(t))}{\log (N(t))}=const log(N(t))log(E(t))=const
2.2 网络直径随时间的变化
网络直径——网络中任意两节点间距离的最大值。
Diameter shrinks over time——我们会发现,网络直径随着网络的演化变小了。随着网络的增长,节点之间的距离逐渐减小。比如说,如果你只认识A的大学同学的高中同学的小学同学,你想认识A,你只能通过3个人的介绍;而如果有一天你认识了A的初中同学,或者有一天认识了A的大学同学的高中同学,你只需要通过更少的人就可以认识A——你和A之间的距离(直径)变小了。
导致这种变化的原因有两个——致密性(density)的变化和degree sequence的变化。

2.3 网络度分布(degree distribution)随时间的变化
How does degree distribution evolve to allow for densification?——degree和densification的关系。
(1)若度演化指数 γ t \gamma_t γt为常数。
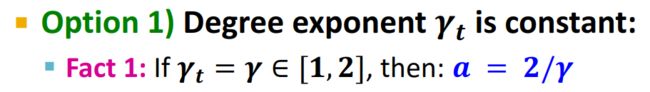

(2)若度演化指数 γ t \gamma_t γt随着网络的规模变化:

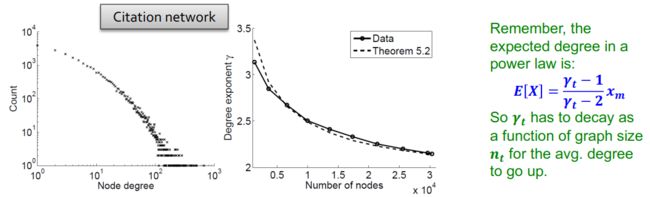
2.4 Forest fire model
Forest fire model(森林火灾模型)主要用于模拟随着时间的演化,致密性增加,网络直径降低的图。这个模型的idea可以从社交关系去理解,当你参加一个晚会时,你可以先认识一个朋友,然后通过这个朋友不断地去结交新的朋友。
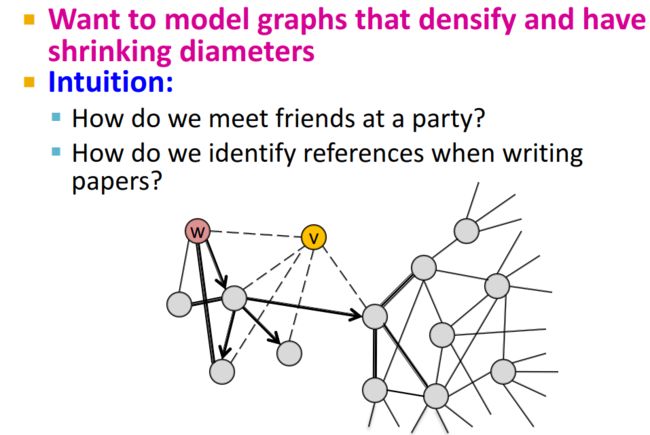
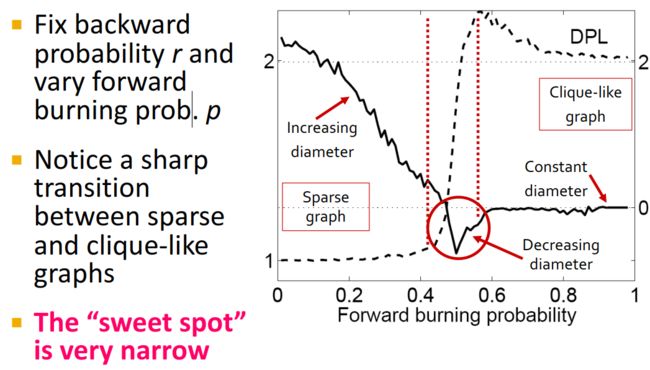
在Forest fire model中有两个重要的参数:
- p p p——向前传递的概率
- r r r——向后传递的概率
该模型的演化流程如下:
- v v v chooses an ambassador node w w w uniformly at random, and forms a link to w w w——新加入一个节点 v v v,随机选择一个节点 w w w并与其连接—— v v v先认识了一个朋友 w w w
- generate two random numbers x x x and y y y from geometric distributions with means p ( 1 − p ) p(1-p) p(1−p) and r p ( 1 − r p ) rp(1-rp) rp(1−rp)——根据服从参数 p p p和参数 r r r的几何分布随机选择两个数 x x x和 y y y,使其平均分别为 p ( 1 − p ) p(1-p) p(1−p) r p ( 1 − r p ) rp(1-rp) rp(1−rp)——相当于随机选取 x x x个 w w w认识的人和 y y y个认识 w w w的人。
- v v v selects x x x out-links and y y y in-links of w w w incident to nodes that were not yet visited and form out-links to them——选取 w w w的 x x x个out-links与 y y y个 in-links 与 v v v相连——相当于 v v v通过 w w w,认识了 x x x个 w w w认识的人,并且认识了 y y y个认识 w w w的人。
- v v v applies step (2) to the nodes found in step (3)——对第三步新加入的节点重复第二步的操作,直至没有新节点加入为止——即 v v v继续通过 w w w的朋友去认识新的人
如果 p p p和 r r r这两个参数选取的很好的话,可以得到符合预期的模拟结果:
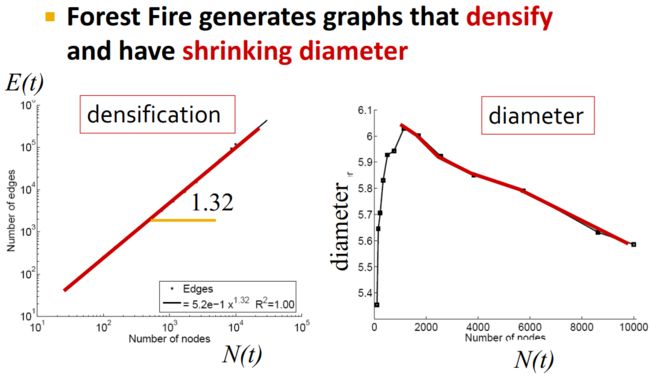

但是符合要求的 p p p或者 r r r的参数取值范围很小:
3. Temporal Networks 含时网络/时序网络
一份介绍含时网络的PPT
Temporal Networks 刻画的是一组固定的节点之间的关联随时间的演化。

在时序网络中,节点之间的连边都带有时间戳,这个时间戳这条边出现的时间。

例子:
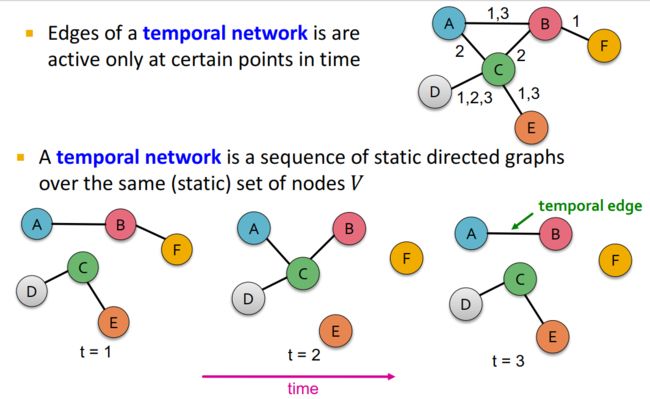
4. Microscopic Evolution of Networks
我们这一节讨论微观角度下的网络演化。微观角度下我们主要关注边随时间变化的演化及其对网络上信息传递的影响。那么,我们基于时序网络,考虑下面两个问题:
- How do we define paths and walks in temporal networks?
- How can we extend network centrality measures to temporal networks?
4.1 Temporal path
Temporal path是带有时间戳的边的序列,在这个序列中,随着时间的演化,每个节点只被访问一次。例如下图中, [ ( 5 , 2 ) ( 2 , 1 ) ] [(5,2)(2,1)] [(5,2)(2,1)]就是在时间序列 t 1 t_1 t1和 t 3 t_3 t3下就是一条Temporal path。
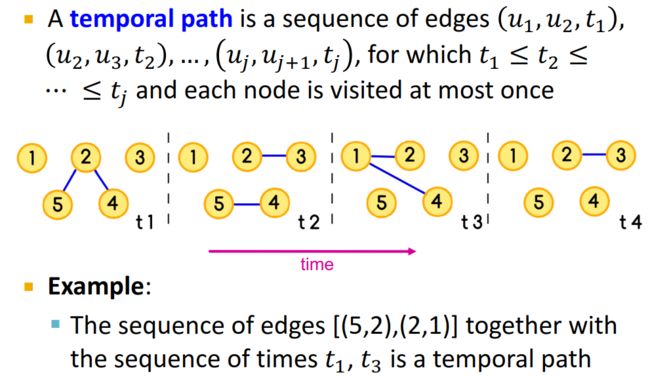
可以通过Dijkstra算法的变种找到Temporal path——

这个算法可以参考论文Efficient Temporal Shortest Path Queries on Evolving Social Graphs。
Temporal Closeness——度量一个节点在时间间隔 [ 0 , t ] [0,t] [0,t]内与网络中任何其他节点的距离。
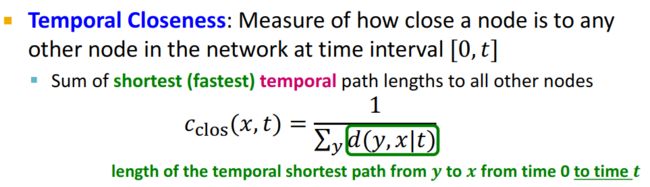

4.2 Temporal PageRank
我们知道,PageRank是对网页影响力的排名。但是,随着时间的演化,有些网站的影响力就大不如从前了(比如之前很火的人人网,现在已经销声匿迹了)。这种加上时间演化因素的PageRank就是Temporal PageRank。
我们首先先来看一下Temporal walk的定义——
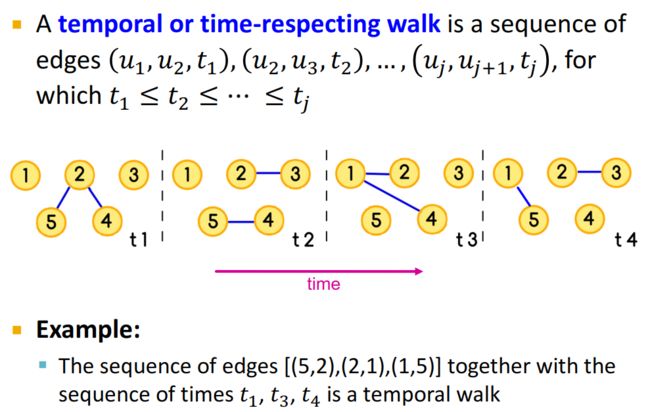
那么,我们将PageRank中的random walk和Temporal walk结合——idea of Temporal PageRank: Make a random walk only on temporal or time-respecting paths
关于这一部分,可以参考两篇论文:
Temporal PageRank
Temporal PageRank on Social Networks
5. Mesoscopic Evolution of Networks
这部分课上没有怎么讲,可以看另一份笔记,我觉得比我写得好:图机器学习 - cs224w Lecture 15 - 网络演变