论文阅读《P-MVSNet: Learning Patch-wise Matching Confidence Aggregation for Multi-View Stereo》

论文地址：P-MVSNet: Learning Patch-wise Matching Confidence Aggregation for Multi-View Stereo

一、摘要

  Cost Volumes 应该是各向异性的，但是传统的方法使用各向同性的方式来处理它（基于方差计算，每个像素都以相同的贡献度参加代价聚合计算），文章使用了一个各向同性的3D卷积和各向异性的3D卷积相结合的代价聚合方式得到更加鲁棒的代价体。

二、网络结构

2.1 特征提取

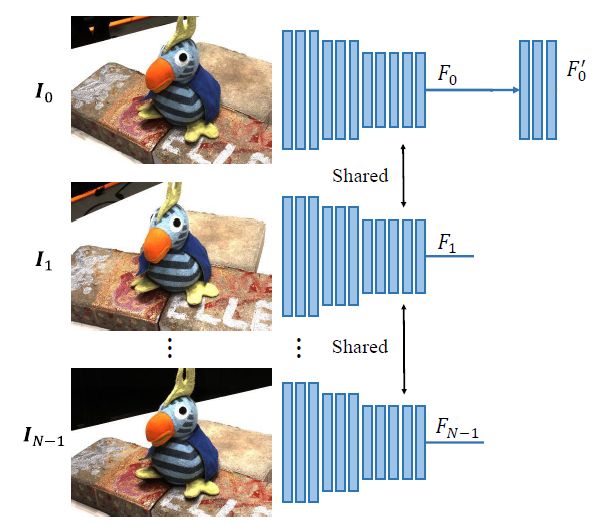
  与MVSNet一样，经过卷积神经网络提取参考图像和N-1张源图像的特征$F_i\in {\mathbb{R}}^{\frac{H}{4}\times \frac{W}{4}\times C}$,其中$i\in (0,N-1)$，将参考视图经过Decoder得到参考视图的引导特征图$F_0^{\prime }\in {\mathbb{R}}^{\frac{H}{2}\times \frac{W}{2}\times C}$,其中$\{F_i{\}}_1^{N-1}$用于后面构建Matching Confidence Volume（MCV），而$F_0^{\prime }$用于引导生成更高分辨率的深度图。

2.2 基于patch的可学习匹配代价置信度计算

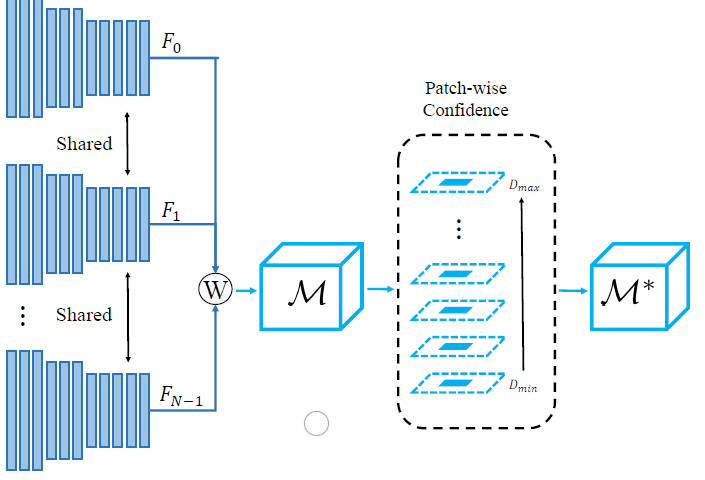
  匹配代价体计算：将源视图的特征图经过相机的内外参数warp到参考视图，然后基于L2距离计算匹配代价体，如式1所示：
$$\mathcal{M}(d,\mathbf{p},c)=\exp \left(-\frac{{\sum }_{j=1}^{N-1}{\left(F_j\left({\mathbf{p}}^{\prime },c\right)-F_0(\mathbf{p},c)\right)}^2}{N-1}\right)\text{\hspace{1em}(1)}$$
其中，$j$ 代表不同视图，$p$ 代表参考帧的像素点坐标，$c$ 代表特征的维度， $p^{\prime }$ 表示邻域帧中 $p$ 点对应的像素坐标点。
  代价聚合：
$${\mathcal{M}}^a(d,\mathbf{p},c)={\rho }_1(\mathcal{M}(d,\mathbf{p},c))+{\rho }_2\left({\Omega }_1(\mathcal{M}(d,\mathbf{p},c))\right)\text{\hspace{1em}(2)}$$
其中：${\rho }_1$ 就是将 $p$ 点的特征值乘以一个1x1x1的卷积核（一个尺度因子），${\Omega }_1$ 表示1x3x3的卷积+BN+RELU，表示将 $p$ 点邻域的像素聚合，但只在同一个深度层聚合，因为卷积核的第一维为1，该卷积核的参数为ρ1。
$${\mathcal{M}}^{\star }(d,\mathbf{p},c)=\tanh \left({\rho }_3\left({\Omega }_2\left({\mathcal{M}}^a(d,\mathbf{p},c)\right)\right)\right)\text{\hspace{1em}(3)}$$
其中：逐深度进行代价聚合之后，沿着深度方向也进行聚合，${\Omega }_2$ 代表3x3x3的卷积核，在 $p$ 点的深度再考虑上下两个深度的3x3的邻域内做代价聚合。卷积核的参数为 ${\rho }_3$，最后乘以一个非线性因子tanh得到代价聚合后的${\mathcal{M}}^{\star }(d,\mathbf{p},c)$.

2.3 hybrid 3D U-Net

  将${\mathcal{M}}^{\star }(d,\mathbf{p},c)$送入到hybrid 3D U-Net得到latent probability volume（LPV）记为$V_2=V_2(d,p)\in (Z\times \frac{H}{4}\times \frac{W}{4})$，表示表示 $F_0$ 每个像素在深度方向上的潜在概率分布。网络由多个各向异性的3D卷积核各向同性的3D卷积组成。浅层使用各向异性的卷积核融合代价体，深层使用各向同性的卷积核来融合更多的信息（各向异性的卷积指的是三个维度不相等的卷积核，各向同性的卷积核指的是三个维度相同的卷积核，感觉有点强行凑观点的嫌疑哈哈哈）。

2.4 深度图计算

  先将$V_2$经过在深度维度上做softmax得到一个概率体 $P_2$，基于期望计算深度图：
$$D_{{\ell }_2}(\mathbf{p})=\sum _{d=D_{\min }}^{D_{\max }}d\cdot {\mathcal{P}}_2(d,\mathbf{p})\text{\hspace{1em}(4)}$$

  $D_{{\ell }_2}$是分辨率较低的深度图，使用参考图像的特征图 $F_0^{\prime }$ 来引导生成高分辨率的深度图。首先将 $F_0^{\prime }$ 与 上采样后的$V_2$ concat成通道为$C+Z$的输入，再经过一个CNN+BN+RELU和一个softmax和期望回归层，输入高分辨率的深度图$D_{{\ell }_1}$；

三、损失函数

  损失函数如下：
$$\begin{array}{rl}\text{ Loss }=& \frac{\alpha }{\left|{\Phi }_2\right|}\sum _{p\in {\Phi }_2}{\Vert D_{{\ell }_2}(p)-D_{{\ell }_2}^{\star }(p)\Vert }_1+\frac{1-\alpha }{\left|{\Phi }_1\right|}\sum _{\mathbf{p}\in {\Phi }_1}{\Vert D_{{\ell }_1}(\mathbf{p})-D_{{\ell }_1}^{\star }(\mathbf{p})\Vert }_1\end{array}\text{\hspace{1em}(5)}$$
其中，${\Phi }_2$和${\Phi }_1$表示有标签的像素点，$D_{{\ell }_1}^{\star }$和$D_{{\ell }_2}^{\star }$表示对应的Ground truth深度图；$\alpha$是一个可调节的权重超参数；

四、深度图滤波

4.1 基于深度估计置信度

  当聚合代价体的深度方向上是单峰时的置信度是最高的。因此，使用初始深度图前的概率体求深度图$D_{{\ell }_2}$的置信度图$C_2(p)$：
$$C_2(\mathbf{p})=\max \left\{{\mathcal{P}}_2(d,\mathbf{p})\mid d\in \left[D_{\min },D_{\max }\right]\right\}\text{\hspace{1em}(6)}$$
  将$C_2(\mathbf{p})$上采样后为$U_1$，计算深度图$D_{{\ell }_1}$的置信度图如式7所示：
$$C_1(\mathbf{p})=U_1(\mathbf{p})+\max \left\{{\mathcal{P}}_1(d,\mathbf{p})\mid d\in \left[D_{\min },D_{\max }\right]\right\}\text{\hspace{1em}(7)}$$
  使用深度估计置信度图来进行滤波，去除置信度低的像素点。

基于深度一致性

  利用了传统方法中的左右一致性检查；
$$\begin{gathered} \left|{\mathbf{q}}^{\prime }-\mathbf{p}\right|<ϵ \\ \frac{\left|\hat{d}\left({\mathbf{q}}^{\prime }\right)-\hat{d}(\mathbf{p})\right|}{\hat{d}(\mathbf{p})}<\eta \text{\hspace{1em}(8)} \end{gathered}$$

五、实验结果