k近邻法（KNN）原理小结

本博客中使用到的完整代码请移步至: 我的github：https://github.com/qingyujean/Magic-NLPer，求赞求星求鼓励~~~

---

适用问题：多类分类、回归

模型特点：特征空间，样本点

模型类型：判别模型

损失函数：-

学习策略：-

学习算法：-

1. k 近邻法算法

k-nearest neighbors （k-NN），k 近邻法，用于分类和回归。

KNN做回归和分类的主要区别在于最后做预测时候的决策方式不同，KNN做分类预测时，一般是使用多数表决法；KNN做回归时，一般是使用平均法，即最近的K个样本的样本输出的平均值作为回归预测值。本文以分类算法展开介绍。

k-近邻法没有显示的学习过程，是一种lazy learning algorithm。

k-近邻法的输入：实例的特征向量，对应于特征空间的点，输出：实例的类别。

k-近邻法：利用训练数据集对特征向量空间进行划分，并作为其分类的“模型”。分类时，对于新实例，根据其 k 个最近邻的训练实例的类别，通过多数表决等方式进行预测。

k-近邻模型的三要素：k值的选择、距离度量（作为"最邻近"的衡量标准）、分类决策规则（例如”多数表决“）

knn算法可总结为3个步骤：

• 1.Choose the number of k and a distance metric.
• 2.Find the k-nearest neighbors of the sample that we want to classify.
• 3.Assign the class label by majority vote.

2. k 近邻法模型

k近邻法使用的模型，实际上对应于特征空间的划分。

模型三要素：k值的选择、距离度量（作为"最邻近"的衡量标准）、分类决策规则（例如”多数表决“）

2.1 k值的选择

k值的选择会对k近邻法的结果产生重大影响。应用中，k值一般取 较小 的数值，通常可使用 交叉验证法 来取得最优的k值。

• k值过小，近似误差会减小，但估计误差会增大。划分粒度变细，模型越复杂，容易发生过拟合。对邻近点非常敏感。
• k值过大，估计误差减小，但近似误差会增大，模型变得过于简单（考虑极端情况k等于训练样本数，预测就只是简单的为类别最多的那一类），与输入实例相距较远（不相似）的训练实例也会对其产生影响。

k 值的选择反映了对近似误差和估计误差之间的权衡。

近似误差，可以理解为对现有训练集的训练误差。更关注于“训练”。
估计误差：可以理解为对测试集的测试误差。更关注于“测试”、“泛化”。

2.2 距离度量

特征空间中2个实例点的距离，是2个实例点 相似程度 的反映。

不同的距离度量所确定的最近邻点是不同的。

设特征空间 $\chi$ 是 n维实数向量空间${\text{R}}^n$，$x_i,x_j\in \chi$，则$x_i,x_j$的$L_p$距离（或叫Minkowski distance）定义为：

$$L_p(x_i,x_j)=(\sum _{l=1}^n|x_i^{(l)}-x_j^{(l)}{|}^p{)}^{\frac{1}{p}},p\ge 1$$

• 当 $p=2$ 时，称为欧氏距离（Euclidean distance）：即

  $L_2(x_i,x_j)=(\sum _{l=1}^n|x_i^{(l)}-x_j^{(l)}{|}^2{)}^{\frac{1}{2}}$

• 当 $p=1$ 时，称为曼哈顿距离（Manhattan distance），即

  $L_1(x_i,x_j)=(\sum _{l=1}^n|x_i^{(l)}-x_j^{(l)}|)$

• 当 $p=\infty$ 时，它是各个坐标距离的最大值，即

  $L_{\infty }(x_i,x_j)=\underset{l}{\max }|x_i^{(l)}-x_j^{(l)}|$

2.3 分类决策规则

多数表决法，多数表决规则等价于经验风险最小化（经验风险：模型关于训练集的平均损失）。

3. k 近邻法实现：kd（k-dimension）树

k近邻法，主要考虑的问题：如何对训练数据进行快速k近邻搜索。尤其是特征空间维数大以及训练数据量大时，尤为重要。

简单实现：线性扫描。需要计算输入实例与每个训练实例的距离。训练集很大时，计算非常耗时，不可取。

kd树实现，提高k邻近搜索效率，以特殊的结构（例如kd tree，还有很多其他方法）存储训练数据，减少了计算距离的次数。

【注意】：kd 树中的k 是指样本特征的维度，KNN中的k是指k个最近的样本实例。

3.1 构造kd树

kd 树是一种对 k 维空间的实例点进行存储以便对其进行快速检索的树形数据结构。kd 树是二叉树，表示对 k 维空间的一个划分。kd 树的每个结点对应一个 k 维的超矩形区域。

通常，依次选择坐标轴对空间切分（或者分别计算n个特征的取值的方差，然后取方差最大的第k维特征n_k对应的坐标轴来对空间进行切分（改进方法））。选择切分点时 为训练实例点在对应坐标轴上（投影）的中位数，这样得到的kd 树是平衡的。注意：平衡的kd 树搜索时的效率未必是最优的。

kd 树的本质其实就是 二叉搜索树 。

3.2 搜索kd树

利用kd 树，搜索可以限制在空间的局部区域上，可以省去对大部分数据点的搜索，从而减少搜索的计算量（主要是由于很多样本点所在的超矩形区域和超球体不相交，根本不需要计算距离）。

kd 树搜索的平均计算复杂度是 O(logN)，N为训练实例数。kd 树适合于 N >> k 的情况，当 N ~ k 接近时，效率寻找下降，几乎接近 线性扫描。

3.3 kd 树预测

kd树的预测：在kd树搜索最近邻的基础上，我们选择到了第一个最近邻样本，就把它置为已选。在第二轮中，我们忽略置为已选的样本，重新选择最近邻，这样跑k次，就得到了目标的K个最近邻，然后根据多数表决法，如果是KNN分类，预测为K个最近邻里面有最多类别数的类别。如果是KNN回归，用K个最近邻样本输出的平均值作为回归预测值。

4. 代码示例

可用于分类和回归任务，下面的示例：使用KNN完成鸢尾花分类任务。

引入包和加载数据：

from matplotlib import pyplot as plt
from matplotlib.colors import ListedColormap

from sklearn import datasets
from sklearn.model_selection import train_test_split
import numpy as np
from sklearn.neighbors import KNeighborsClassifier

iris = datasets.load_iris()
print(iris['data'].shape, iris['target'].shape) # (150, 4) (150,)
X = iris.data[:,[2,3]]
y = iris.target
print('Class labels:', np.unique(y))
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1, stratify=y)
print(X_train.shape, y_train.shape)

输出：

(150, 4) (150,)
Class labels: [0 1 2]
(105, 2) (105,)

绘制决策边界函数：

# 训练，并绘制分类决策边界：
def plot_decision_regions(X, y, classifier, test_idx=None, resolution=0.02):
     # setup marker generator and color map
     markers = ('s', 'x', 'o', '^', 'v')
     colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
     cmap = ListedColormap(colors[:len(np.unique(y))])

     # plot the decision surface
     x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
     x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
     xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
                            np.arange(x2_min, x2_max, resolution))
     Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
     Z = Z.reshape(xx1.shape)
     plt.contourf(xx1, xx2, Z, alpha=0.3, cmap=cmap)
     plt.xlim(xx1.min(), xx1.max())
     plt.ylim(xx2.min(), xx2.max())

     for idx, cl in enumerate(np.unique(y)):
         plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1],
         alpha=0.8, c=colors[idx],
         marker=markers[idx], label=cl,
         edgecolor='black')

     # highlight test samples
     if test_idx:
         # plot all samples
         X_test, y_test = X[test_idx, :], y[test_idx]
         plt.scatter(X_test[:, 0], X_test[:, 1],
                     c='', edgecolor='black', alpha=1.0,
                     linewidth=1, marker='o',
                     s=100, label='test set')

训练：

# 标准化数据
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
sc.fit(X_train)
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)

X_combined_std = np.vstack((X_train_std, X_test_std))
y_combined = np.hstack((y_train, y_test))

# 训练，k=5, 距离度量为
knn = KNeighborsClassifier(n_neighbors=5, p=2, metric='minkowski')
knn.fit(X_train_std, y_train)

print('Training accuracy:', knn.score(X_train_std, y_train))
print('Testing accuracy:', knn.score(X_test_std, y_test))

输出：

Training accuracy: 0.9619047619047619
Testing accuracy: 1.0

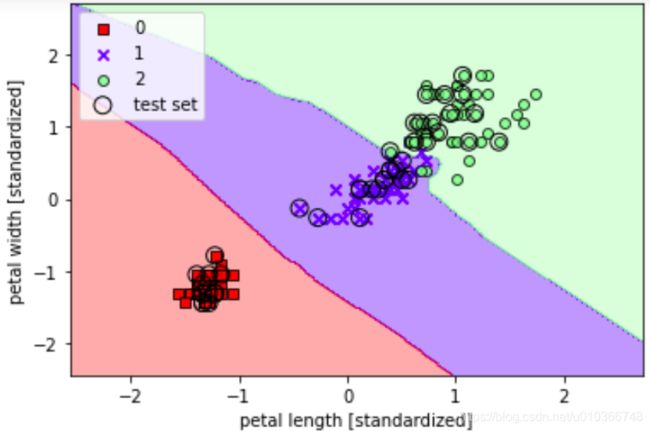
绘制决策边界：

# 绘制决策边界
plot_decision_regions(X_combined_std, y_combined, classifier=knn, test_idx=range(105,150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.show()

5. 模型评价

模型评价参考自刘建平老师的K近邻法(KNN)原理小结。

KNN简单、直观，其主要优点有：

• 1） 理论成熟，思想简单，既可以用来做分类也可以用来做回归
• 2） 可用于非线性分类
• 3） 训练时间复杂度比支持向量机之类的算法低，仅为O(n) （建树的过程）
• 4） 和朴素贝叶斯之类的算法比，对数据没有假设，准确度高，对异常点不敏感
• 5） 由于KNN方法主要靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合
• 6）该算法比较适用于样本容量比较大的类域的自动分类，而那些样本容量较小的类域采用这种算法比较容易产生误分

KNN的主要缺点有：

• 1）计算量大，尤其是特征数非常多的时候
• 2）样本不平衡的时候，对稀有类别的预测准确率低
• 3）kd树，球树之类的模型建立需要大量的内存
• 4）使用懒散学习方法（a lazy learning algorithm），基本上不学习，导致预测时速度比起逻辑回归之类的算法慢
• 5）相比决策树模型，KNN模型可解释性不强

完整代码地址

完整代码请移步至: 我的github：https://github.com/qingyujean/Magic-NLPer，求赞求星求鼓励~~~

最后：如果本文中出现任何错误，请您一定要帮忙指正，感激~

参考

[1] 统计学习方法（第2版） 李航
[2] K近邻法(KNN)原理小结   刘建平
[3] Python_Machine_Learning_2nd_Edition