【图像特征提取】灰度共生矩阵GLCM

参考链接：图像纹理——灰度共生矩阵
知乎——提取图像的颜色、纹理特征(传统算法)

灰度共生矩阵（Gray-level Co-occurrence Matrix，GLCM）原理

灰度共生矩阵可反映灰度 值 和 空间 分布情况。
共生矩阵 $P$ 的描述方法：
规定一个方向（如水平，垂直，对角线）和距离（一个像素、两个像素），矩阵中 $P_{ij}$ 的值由灰度为 $i$ 和 $j$ 的像素对在该方向和距离上出现的次数除以N得到（归一化），N为对P有贡献的像素对总数。
共生矩阵的大小为 $L\ast L$ ，$L$ 是图像灰度级数目。

例子

在图像中任意一点$(x,y)$及偏离它的一点$(x+a,y+b)$ (其中 $a，b$ 为整数) 构成像素点对。

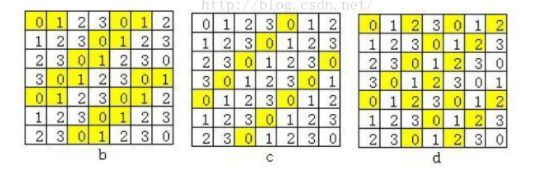
a为原灰度图像，灰度级数为16。为了表示方便，将灰度范围减小到4级，即为下图中样式

若取 a=1，b=0，即统计水平方向上相距为1像素的像素对出现的个数，这里的坐标系为

图b中黄色部分为图e中像素值对（1,0）的个数值


这是图e中（1,2）位置所对应的像素对

同理，图f为左下角方向一个位置相应灰度值对应的矩阵；图g为右侧方向两个像素对应的矩阵。

对比可以看出，图e中(0,1),(1,2),(2,3)和(3,0)均有较高的出现频数。图b表明，图像中存在明显的左上右下方向的纹理。

a，b取值较小对应于变化缓慢（粗而规则）的纹理图像，其灰度共生矩阵对角线上的数值较大。纹理的变化越快（细而规则），则对角线上的数值越小，而对角线两侧的值增大。

灰度共生矩阵特征

由于灰度共生矩阵的数据量较大，一般不直接作为区分纹理的特征，而是基于它构建的一些统计量作为纹理分类特征。Haralick曾提出了14种基于灰度共生矩阵计算出来的统计量：即：能量、熵、对比度、均匀性、相关性、方差、和平均、和方差、和熵、差方差、差平均、差熵、相关信息测度以及最大相关系数。

对比度 Contrast

度量矩阵的值是如何分布和图像中局部变化的多少，反应了图像的清晰度和纹理的沟纹深浅。纹理的沟纹越深，反差越大，效果越清晰；反之，对比值小，则沟纹浅，效果模糊。
反映某像素值及其领域像素值亮度的对比情况，图像亮度值变化快，换句话说纹理较深，它的对比度就越大，也就是它的纹理越清晰。

能量 Energy

能量变换反映了图像灰度分布均匀程度和纹理粗细度。若灰度共生矩阵的元素值相近，则能量较小，表示纹理细致；若其中一些值大，而其它值小，则能量值较大。能量值大表明一种较均一和规则变化的纹理模式。

熵 Entropy

图像包含信息量的随机性度量。当共生矩阵中所有值均相等或者像素值表现出最大的随机性时，熵最大；因此熵值表明了图像灰度分布的复杂程度，熵值越大，图像越复杂。

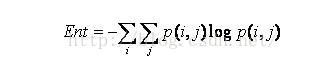
同质性/逆差距 Homogeneity

逆方差反映了图像纹理局部变化的大小，若图像纹理的不同区域间较均匀，变化缓慢，逆方差会较大，反之较小。与对比度或相异性相反，同质性的权重随着元素值与对角线的距离而减小，其减小方式是指数形式的。

相关性 Correlation

用来度量图像的灰度级在行或列方向上的相似程度，因此值的大小反应了局部灰度相关性，值越大，相关性也越大。

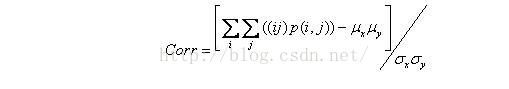
MATLAB代码

glcm = graycomatrix(I)

​glcms = graycomatrix(I,param1,val1,param2,val2,...)

​[glcms,SI] = graycomatrix(...)

关注的像素与其邻点之间的距离通过Offsets来进行调整，比如[0 1]代表是水平方向，[-1 1]代表是右上角45度方向，[-1 0]代表是竖直方向，即90度方向，而[-1 -1]则代表是左上角，即135度方向

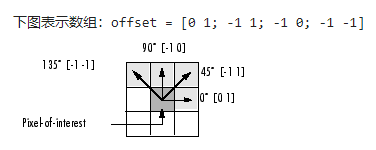
这里的坐标系为水平向右为Y轴正方向，垂直向下为X轴正方向。