Review of Algorithm (HITSZ) 含22年真题回忆

1. Time Analysis

1.1 Basic

NOTE:

1. $lo{g}_{a}b=\frac{lo{g}_{c}b}{lo{g}_{c}a}$
2. $lgn=lo{g}_{2}n$

• $p(n)=O(f(n))$

  $p(n)\le cf(n)$.

• $p(n)=\Omega (f(n))$

  $p(n)\ge cf(n)$

• $p(n)=\Theta (f(n))$

  $c_{1}f(n)\le p(n)\le c_{2}f(n)$

• $p(n)=o(f(n))$

  $p(n)<cf(n)$

• $p(n)=\omega (f(n))$

  $p(n)>cf(n)$

Solution: Calculating $li{m}_{n\to \infty }\frac{p(n)}{f(n)}$.

• If $li{m}_{n\to \infty }\frac{p(n)}{f(n)}=a\ne 0$, $p(n)=\Theta (f(n))$
• If $li{m}_{n\to \infty }\frac{p(n)}{f(n)}=t\le a$, $p(n)=O(f(n))$, since $\frac{p(n)}{f(n)}<\delta +t\le \delta +a$.
• If $li{m}_{n\to \infty }\frac{p(n)}{f(n)}=t\ge a$, $p(n)=\Omega (f(n))$, since $\frac{p(n)}{f(n)}>t-\delta \ge a-\delta$
• If $li{m}_{n\to \infty }\frac{p(n)}{f(n)}=0$, $p(n)=o(f(n))$, since $\frac{p(n)}{f(n)}<\delta$.
• If $li{m}_{n\to \infty }\frac{p(n)}{f(n)}=\infty$, $p(n)=\omega (f(n))$, since $\frac{p(n)}{f(n)}>N_0$.

1.2 Master Method

Given equation like $T(n)=aT(\frac{n}{b})+f(n)$

• If $f(n)=O(n^{lo{g}_b(a)-ϵ})$, $T(n)=\Theta (n^{lo{g}_b(a)})$
• If $f(n)=\Theta (n^{lo{g}_b(a)})$, $T(n)=\Theta (n^{lo{g}_b(a)}\ast lgn)$
• If $f(n)=\Omega (n^{lo{g}_b(a)+ϵ})$, and $af(n/b)\le cf(n),\exists c<1$, then $T(n)=\Theta (f(n))$

1.3 Recurrence Problems

• Big Integer Multiplication
  $$XY=ac{2}^n+(ab+cd)2^{n/2}+bd$$
  Time complexity:
  $$T(n)=4T(n/2)+O(n)$$

  Divide and conquer:
  $$XY=ac{2}^n+((a+c)(b+d)-ac-bd)2^{n/2}+bd$$
  Time complexity:
  $$T(n)=3T(n/2)+O(n)$$

• FFT

• Chess Board Cover

  Put the “L” into center.

• Binary Search

2. Sorting Algorithm

2.1 Comparing Sort

2.1.1 Insertion Sort

Insert a number into a sorted array. Need to move the element.

Time complexity:
$$T(n)=\sum _{i=1}^{i=n}(i-1)=O(n^2)$$

2.1.2 Merge Sort

Divide the array into two parts, sort them separately and merge them

Time complexity:
$$T(n)=2T(\frac{n}{2})+O(n)$$
According to master method: $a=2,b=2,f(n)=cn$. Thus $n^{lo{g}_{b}a}=n=\Theta (n)$. So that
$$T(n)=\Theta (nlgn)$$

2.1.3 Shell Sort

希尔排序动图_哔哩哔哩_bilibili

Time complexity:
$$\approx O(N^{1.25})$$

2.1.4 Lower boundary of comparison sort

$$\Theta (nlgn)$$

2.2 Linear Sort

2.2.1 Counting Sort (Stable)

• Flow:

  • Input array $A$.
  • Assigning 0 to array $C$. ($O(k)$)
  • Counting each element in an array $A$, recording in $C$. ($O(n)$)
  • Accumulating array $C$. ($O(k)$)
  • Sorting in array $B$. ($O(n)$)

• Time complexity: $O(n+k)$, where $n$ is the input number, $k$ is equivalent to value of the maximal number.

2.2.2 Radix Sort (Stable)

• Run Counting Sort in group
• Time complexity: $O(\frac{b}{r}(n+2^r))=O(n)$. Where $b$ is the bits number of the compared numbers, $r$ is the bits number of per group number. Thus there are $\frac{b}{r}$ groups. We do not want $r>lgn$.

2.2.3 Bucket Sort

• Divide input array into several buckets, running insert sort in each bucket and concatenate them together.
• Expected time: $\Theta (n)$
• Worst-case performance: $O(n^2)$
• How to improve? Change insert sort to other efficient sort. Like, merge sort.

3. Hash Table

3.1 Hash method

• Division method: $h(k)=k\mathrm{m}\mathrm{o}\mathrm{d}m$. Do not choose $m=2^r$, this not uses all of bits in $k$.
• Multiplication method: $h(k)=(Ak\mathrm{m}\mathrm{o}\mathrm{d}{2}^r)rsh(w-r)$. $A$ is an odd integer in the range $2^{w-1}\le A\le 2^w$
• An unsuccessful search requires: $1+\alpha$, where $\alpha =m/n$, refer to load factor.

3.2 Collision

NOTE:

1. $A\mathrm{m}\mathrm{o}\mathrm{d}B=A-(A÷B)\ast B$
2. $(A+B)\mathrm{m}\mathrm{o}\mathrm{d}N=(A\mathrm{m}\mathrm{o}\mathrm{d}N+B\mathrm{m}\mathrm{o}\mathrm{d}N)\mathrm{m}\mathrm{o}\mathrm{d}N$

• Assuming $h(k)=k\mathrm{m}\mathrm{o}\mathrm{d}m$.
• Learning probing: $h^{\prime }(k,i)=(k\mathrm{m}\mathrm{o}\mathrm{d}m+i)\mathrm{m}\mathrm{o}\mathrm{d}m$
• Quadratic probing: $h^{\prime }(k,i)=(k\mathrm{m}\mathrm{o}\mathrm{d}m+c_{1}i+c_2{i}^2)\mathrm{m}\mathrm{o}\mathrm{d}m$
• Double hash probing: $h^{\prime }(k,i)=(k\mathrm{m}\mathrm{o}\mathrm{d}m+i\ast h_2(k))\mathrm{m}\mathrm{o}\mathrm{d}m$
• Theorem: Open-addressed hash table with load factor $\alpha$, the expected number of probes in an unsuccessful search is at most $1/(1-\alpha )$ . That is to say:
  • If the table is half full, then the expected number of probes is $1/(1–0.5)=2$.
  • If the table is 90% full, then the expected number of probes is $1/(1–0.9)=10$.

4. BST

4.1 Normal BST

• Left subtree is less than root

• Right subtree is large than root

• Deletion:

  • No children: Delete directly.
  • One child: Delete and make the child as the parent’s child.
  • Two child: Replace with the successor. Apply 1 or 2 to delete it.

• Randomly built BST has $O(lgn)$ search time complexity.

4.2 Treap

Treap is the BST with priority. This helps build a randomly BST.

5. RB Tree

• Node is either red or black.
• Root is always black.
• Black height has only one.
• Terminate with two black nodes.
• Red node cannot connect with red node.
• Theorem: A RB tree with $n$ internal nodes has height $h\le 2lg(n+1)$. $h=O(lgn)$.
  • In my opinion, $N\le n+n-1$, so that $h\le lg(2n-1)=O(lgn)$

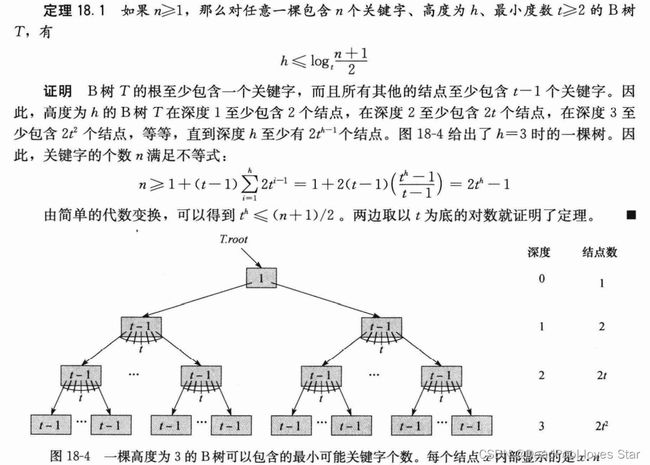
6. B Tree

• Degree $n$ (out degree): allows at least $n-1$ keys, at most $2n-1$ keys.

• Split when insertion.

• $h\le lo{g}_t(\frac{(n+1)}{2})$. See proof below.

• Deletion: Make sure each node has at least $t-1$ keys and merge those nodes can be merged. i.e., both $t-1$.

7. Augmenting Data Structures

• Order-Statistic Tree (OS-Tree): Recording the number of elements of subtree.
• Interval Tree: Each node represents an interval $[a,b]$, and maintains a $max$ field, which satisfies:

$$max=max(\{\begin{array}{r}node.high\\ node.left.max\\ node.right.max\end{array})$$

• Search interval i in the Interval Tree:
  • Check if root is overlapped. If it is overlapped, then return root.
  • Check whether root.left.max ≥ i.left, go to left. Recursively run process.
  • Otherwise, go to right. Recursively run process.

8. Skip Lists

• Each node is promoted with $1/2$ probability.
• Multiple indexing
• Idea: Skip list with $lgn$ linked lists is like a binary tree (B+ tree).
• With high probability, every search in an n-element skip list costs $O(lgn)$

9. Amortized Analysis

9.1 Basic Concept

• Aggregated:
  $$T=\frac{{\sum }_{i=1}^{n}unit}{n}$$

• Accounting: Store $c$ for each normal case operation, and each normal case operation spends $m$. Thus, you store $c-m$ to the bank for each normal case operation. When the cost operation is coming, you spend all of your money in the bank. Make sure that the bank always has positive money.
  $$T=\frac{{\sum }_{i=1}^{n}c}{n}=c$$

• Potential: Design a potential function $\varphi (D_i)$, s.t., $c_i^{\prime }=c_i+\varphi (D_i)-\varphi (D_{i-1})$. Make sure that $\varphi (D_0)=0$, and $\varphi (D_i)\ge 0$

9.2 Examples

9.2.1 Dynamic tables

• Aggregated
  $$c_i=\{\begin{array}{r}i,i-1=2^n\\ 1,otherwise\end{array}$$

  $$\sum _{i=1}^n{c}_i\le n+\sum _{j=1}^{lg(n-1)}{2}^j\le 3n=\Theta (n)$$

  Thus,
  $$c_i^{\prime }=\Theta (n)/n=\Theta (1)$$

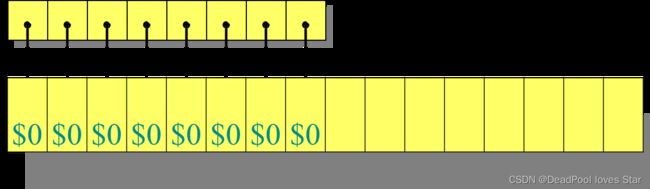
• Accounting

  Charge $c_i^{\prime }=3$ for each operation, so that $1$ for insertion, $2$ is stored for extending. When extending the table, $1$ for inserting old item. $1$ for inserting new item. See the figure below

• Potential

  Define
  $$\varphi (D_i)=2i-2^{\lceil lgi\rceil }$$
  So that
  $$c_i^{\prime }=c_i+\varphi (D_i)-\varphi (D_{i-1})$$
  Thus, we have $c_i^{\prime }=3$.

9.2.2 Binary Counter

• Aggregated

  The summation of flip frequency of each bit.
  $$\frac{n}{2}+\frac{n}{4}+\frac{n}{8}+...+\frac{n}{2^n}=2n$$
  So that $c_i^{\prime }=2$.

• Accounting

  Operation $0\to 1$ store $2$, and pay for $1$. Operation $1\to 0$ pay for $1$ store 0. Thus, for $n$ operations, we must store $2n$ fee. Thus $c_i^{\prime }=2$.

• Potential

  Define
  $$\varphi (D_i)=numberof1incounter$$
  Thus,
  $$c_i^{\prime }=c_i+\varphi (D_i)-\varphi (D_{i-1})$$
  Let operation $i$ changes $t_i$ $1$ to $0$. And there only one $0$ is changed to $1$ (But be careful to the situation that the counter is overflow). Thus
  $$\varphi (D_i)\le \varphi (D_{i-1})-t_i+1$$
  So that
  $$c_i^{\prime }\le t_i+1+1-t_i=2$$

10. Dynamic Programming

• Matrix-chain Multiplication

  The minimal multiplication times of $A_1\ast A_2\ast ...\ast A_n$

  Let $Min[i,j]$ denote the minimal multiplication times of $A_i\ast ...\ast A_j$
  $$Min[i,j]=\{\begin{array}{ll}0& \text{ i=j }\\ mi{n}_{i\le k\le j}\{Min[i,j],Min[i,k]+Min[k+1,j]+p_i\ast p_k\ast p_j\}& \text{ i=j }\end{array}$$

• LCS problem

  The longest common sub sequence of $X=x_1{x}_2...x_m$ and $Y=y_1{y}_2...y_n$

  Let $LCS[i,j]$ denote the length of the longest common sequence of $X_i=x1...x_i$ and $Y_j=y_1...y_j$

  Thus,
  $$LCS[i,j]=\{\begin{array}{ll}0& \text{ i=0 or j=0}\\ LCS[i-1,j-1]+1& \text{ Xi=Yj }\\ max\{LCS[i-1,j],LCS[i,j-1]\}& \text{ Xi=Yj }\end{array}$$

• Triangle Decomposition of Convex Polygon

  Find the minimal summation of triangle decomposition.

  Let $Min[i,j]$ denote the minimal summation triangle decomposition of vertex from $i$ to $j$.

  Thus,
  $$Min[i,j]=\{\begin{array}{ll}0& \text{ i=j }\\ mi{n}_{i<k<j}\{Min[i,k]+Min[k,j]+w(v_i{v}_j{v}_k)\}& \text{ i=j }\end{array}$$

11. Greedy Algorithm

11.1 Basic

To prove a greedy algorithm is workable, you should:

• First, show the optimal structure: Given an optimal solution of the problem, prove that it’s subproblem is also optimal. i.e., applying the recursive function like DP problem.
• Second, show that the greedy selection must be in the final optimal solution.

11.2 Examples

• Activities arrangement
• 0-1 Knapsack

12. Linear Programming

• Simplex Algorithm
  • Build the slack form, where each variable is constrained by $\ge 0$.
  • Find the most constrained variable, replacing it with the slack variable. Where slack variable can reach to $0$.
  • Recursive to find the anwser.

13. FFT

To solve a FFT problem, for example:

Compute DFT of input $(x(0),x(1),x(2),x(3),x(4),x(5),x(6),x(7))$ by using FFT

• First, determine leaves. In this example, leaves are

  $(x(0),x(4))$, $(x(2),x(6))$, $(x(1),x(5))$, $(x(3),x(7))$

• Second, draw a butterfly. i.e,

  There are two things you should note:

  1. Recursively. $W_8^0=W_4^0$, $W_8^2=W_4^1$, and $1=W_2^0$
  2. Positive for even number and Negative for odd number.

• Third, compute from leaves, for example
  $$\begin{array}{rl}X(0)& =A(0)+W_8^{0}B(0)\\ & =(C(0)+D(0))+W_8^0(E(0)+F(0))\\ & =(x(0)+x(4)+x(2)+x(6))+W_8^0(x(1)+x(5)+x(3)+x(7))\\ & =\sum _{i=0}^{i=7}x(i)\end{array}$$

14. NP

14.1 P, NP, NPC, NPH

• P: Solve and Verify in polynomial time.

• NP: Verify in polynomial time.

• NP-hard: All NP problems can be reduce to the problem.

• NPC: ① It is a NP problem ② Any NP problem can be reduced to the problem.

• The relations

  • If $NP\ne P$: $NPH$ can be reduced to either $NP$ problems or other $non-P$ problems.
  • If $NP=P$: $NPH$ can be reduce to $NP=P$ problems or other problems. Thus if one problem is $NP$, it is a $NPH$ problem. Thus, it is a $NPC$ problem.

14.2 Solution for NPC problems

• Exponential solution

  • Backtracking (DFS + prune)
  • Dynamic programming

• Approximate algorithm

  • Approximate ratio

    Assume the best solution is $c^{\ast }$, and the approximate solution is $c$. The approximate ratio is:
    $$max\{\frac{c^{\ast }}{c},\frac{c}{c^{\ast }}\}\le \rho (n)$$
    $\rho (n)$ is approximate ratio.

  • Relative error $ϵ(n)$
    $$|\frac{c-c^{\ast }}{c^{\ast }}|\le ϵ(n)$$

15. 2022年真题回忆

选择 + 大题

15.1 选择题

共5题

1. FFT时间复杂度 ($Olgn$)
2. 红黑树插入时间复杂度（$lgn$）
3. B树度为t, 判断关键字数、儿子数
4. 哪种形式是hash的线性探测
5. 忘记了

15.2 大题

1. 树堆（Treap）插入
2. 用FFT计算DFT
3. 递归树计算$T(n)=3T(n/4)+c{n}^2$
4. 线性规划，求解$18x+12.5y$的最大值
5. 证明活动选择问题，选择最晚开始的活动
6. BST与红黑树问题：给一个树形结构填值，使之符合BST；红黑树黑高度为k，最大、最少内部节点数；BST旋转一下变成红黑树
7. B树+Augumenting
8. 动规问题，合并石堆

总的来说不算难，但是第7题的证明题是真难想，希望有分~~