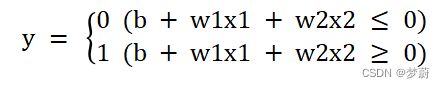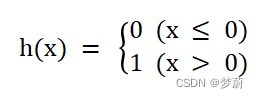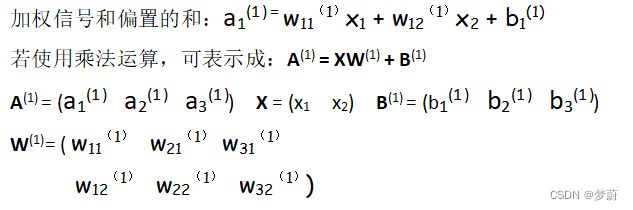深度学习-----课堂笔记

第三章  神经网络

目录

第三章  神经网络

3.1  从感知机到神经网络

3.2  激活函数（activation function）

3.3  多维数组

1）.shape

2）矩阵乘法

3.4  3层神经网络的实现

1）符号确认

2）各层间信号传递的实现

3.5  手写数字识别

1）MNIST数据集

2）神经网路的推理处理

---

3.1  从感知机到神经网络

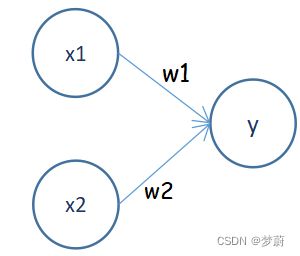
1）简单感知机如图：

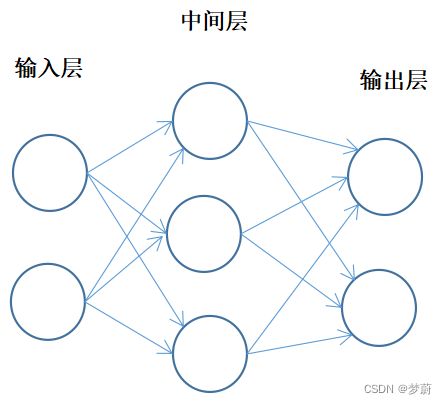
2）神经网络的例子如图：（中间层有时也称隐藏层）

3.2  激活函数（activation function）

1）作用：在于决定如何来激活输入信号的总和；

2）感知机中使用了阶跃函数作为激活函数:

3）神经网络中经常使用的一个激活函数是sigmoid()函数：

#代码实现
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

4）sigmoid()函数与阶跃函数的比较：

   ①平滑性不同，sigmoid()函数较平缓(连续可导)；

   ②返回值不同，阶跃函数只能返回0或1，而sigmoid函数可以返回实数；

   ③具有相似的形状；

   ④两者均为非线性函数；

5）神经网络的激活函数必须为非线性函数，因为使用线性函数的话，加深神经网路的层数时，无法发挥多层网路带来的优势；

3.3  多维数组

1）.shape

①若A是一维数组，有四个元素构成，则A.shape的结果是一个元组（tuple)，因为一维数组的情况下也要返回和多维数组的情况下一致的情况；

②二维数组时返回的是元组(4,3)，三维数组时返回的是元组(4,3,2)，因此一维数组时也同样以元组的形式返回结果。

import numpy as np
A = np.array([1,2,3,4])
print(A)

>>> [ 1 2 3 4 ]

A.shape

>>> (4, ）

2）矩阵乘法

①np.dot(A,B) 对位相乘（对应行乘以对应列）；np.dot(A,B)和np.dot(B,A)的值可能不一样，顺序不同，结果也会不同；

②在多维数组的乘积运算中，两个矩阵中的对应维度的元素个数必须一致；

3.4  3层神经网络的实现

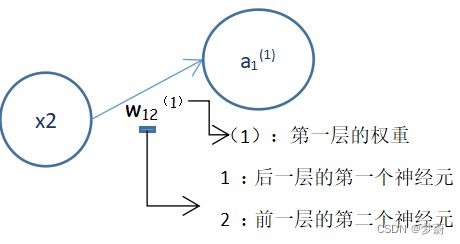
1）符号确认

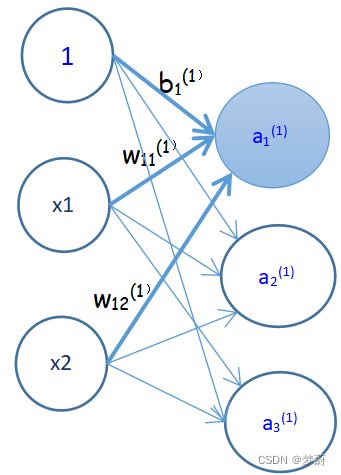
2）各层间信号传递的实现

①输入层到第一层的第一个神经元的信号传递过程：

 ②激活函数的计算过程：（z：a 被激活函数转换后的信号）

#激活函数  
def sigmoid(x):
    return 1/(1 + np.exp(-x))

Z1 = sigmoid(A1)

③第一层到第二层的信号传递过程：第一层的输出变成了第二层的输入，其余实现与上一层相似；

③第二层到输出层的信号传递过程：输出层的实现与上一层相似，但最后的激活函数与之前的隐藏层不同，使用的是softmax()函数;

#softmax函数
def softmax(x):
    x = x-np.max(x)
    exp_sum = np.sum(np.exp(x))   
    return np.exp(x)/exp_sum 

✨【一般地，回归问题可以使用恒等函数（identify_function() ），二元分类问题可以使用 sigmoid() 函数，多元分类问题可以使用 softmax() 函数】

3.5  手写数字识别

1）MNIST数据集

①MNIST手写数字图像集：训练图像有6万张，测试图像有1万张，可用于学习与推理；

②一般使用方法：先用训练图像进行学习，再用学习到的模型度量能在多大程度上对测试图像进行分类；

③MNIST的图像数据是28像素28像素的灰度图像，各个像素的取值在0到255之间。每个图像数据都相应的标有“7” "2" "1" 等标签。

2）神经网路的推理处理

①神经网络的输入层有784个神经元，输出层有10个神经元（784： 2828 784；10：数字0~9，共10个类别）；

②批处理：将输入数据从输入一张图像打包成输入多张图像的情形称为批处理，输入数据的集合称为“批”（batch）；通过以批为单位进行推理处理，能够实现高速的运算；

③代码实现：

#导入numpy包、pickle包
import numpy as np
import pickle

#封装函数

#封装数据集
def load_data():      
    save_file = r"C:\Users\花落随缘\Desktop\魏桂凤\深度学习\mnist.pkl"   #打开mnist.pkl
    with open(save_file, 'rb') as f:        #读取文件
        dataset = pickle.load(f)
    x_train, t_train = dataset["train_img"], dataset["train_label"] #调用训练图像与标签
    x_test, t_test = dataset["test_img"], dataset["test_label"]     #调用测试图像与标签
    return x_test,t_test   #返回训练集预测试集数据

#参数初始化
def init_network():
    network = {}       #字典存放数据
    network["w1"] = np.random.rand(784,50)    #随机返回符合均匀分布的一组为784行，50列的随机样本值；
    network["b1"] = np.random.rand(50)        #随机返回符合均匀分布的50个随机样本值；
    network["w2"] = np.random.rand(50,10)     #随机返回符合均匀分布的一组为50行，10列的随机样本值；
    network["b2"] = np.random.rand(10)        #随机返回符合均匀分布的个10随机样本值；
    return network                            #返回 network
  
#激活函数  
def sigmoid(x):
    return 1/(1 + np.exp(-x))
#softmax函数
def softmax(x):
    x = x-np.max(x)
    exp_sum = np.sum(np.exp(x))   
    return np.exp(x)/exp_sum 

#网络计算过程
def predict(network,x):
    w1,b1,w2,b2 = network["w1"],network["b1"],network["w2"],network["b2"]  #读取数据
    a1 = np.dot(x, w1) + b1      #隐藏层的加权总和
    z1 = sigmoid(a1)             #被激活函数转换后的信号，第一个隐藏层的输出
    a2 = np.dot(z1, w2) + b2     #输出层的加权总和
    y = softmax(a2)              #输出层过softmax()函数
    return y                     #输出y


x_test,t_test = load_data()     #读取数据
x = x_test[0:100]               #选取输出层中1~100张图片，进行批处理
network = init_network()

# 只有一个隐藏层，输入层784，隐藏层50，输出层10
correct = 0       #初始值为0
#批处理
for i in range(0,len(x_test),100):    #范围：[0,10000),步长为100
    x = x_test[i:i+100]          #用for语句逐一取出保存在x中的图像数据；
    y = predict(network,x)       #分类；以Numpy数组的形式输出各个标签对应的概率
    y_label = np.argmax(y,axis = 1)          #返回每行中获取概率最高的元素的索引
    correct = np.sum(y_label == t_test[i:i+100])   #计算准确次数
correct = correct/100           #计算准确率
print("正确率为:",correct)           #打印准确率