吴恩达深度神经网络笔记—TensorFlow入门
TensorFlow入门
了解一个深度学习框架，它将允许您更容易地构建神经网络。像TensorFlow、PaddlePaddle、Torch、Caffe、Keras等机器学习框架可以显著加速机器学习的开发。
学习TensorFlow这个框架：
- 初始化变量
- 建立一个会话
- 训练的算法
- 实现一个神经网络
导入TensorFlow库
import math
import numpy as np
import h5py
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.python.framework import ops
from tf_utils import load_dataset, random_mini_batches, convert_to_one_hot, predict
%matplotlib inline
tf.compat.v1.disable_eager_execution()# 保证sess.run()能够正常运行
np.random.seed(1)
导入了相关的库，将要完成不同的应用，现在看一下下面的计算损失的公式：
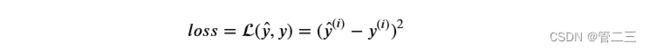
y_hat = tf.constant(36, name='y_hat') # Define y_hat constant. Set to 36.
y = tf.constant(39, name='y') # Define y. Set to 39
loss = tf.Variable((y - y_hat)**2, name='loss') # Create a variable for the loss
init = tf.compat.v1.global_variables_initializer() # When init is run later (session.run(init)),
# the loss variable will be initialized and ready to be computed
with tf.compat.v1.Session() as session: # Create a session and print the output
session.run(init) # Initializes the variables
print(session.run(loss)) # Prints the loss
运行结果：
9
如果发生：module ‘tensorflow’ has no attribute 'Session’等等问题，出现这个问题的原因是所用的tensorflow版本不支持session，版本对不上只需要在代码中加compat.v1
无法执行sess.run()的原因也是tensorflow版本2.0无法兼容版本1.0.添加tf.compat.v1.disable_eager_execution()
分析上述代码。在TensorFlow中编写和运行程序有以下步骤:
- 创建Tensorflow变量（此时，尚未直接计算）
- 实现Tensorflow变量之间的操作定义
- 初始化Tensorflow变量
- 创建Session
- 运行Session，此时，之前编写操作都会在这一步运行。
因此，当我们为损失创建一个变量时，我们只是将损失定义为其他量的函数，而没有计算其值。为了计算它，我们必须运行init=tf. global_variable_initializer()。这初始化了loss变量，在最后一行，我们终于可以求出loss的值并输出它的值。
例子：
a = tf.constant(2)
b = tf.constant(10)
c = tf.multiply(a,b)
print(c)
运行结果：
Tensor("Mul:0", shape=(), dtype=int32)
我们并没有看到结果20，不过我们得到了一个Tensor类型的变量，没有维度，数字类型为int32。我们之前所做的一切都只是把这些东西放到了一个“计算图(computation graph)”中，而我们还没有开始运行这个计算图，为了实际计算这两个数字，我们需要创建一个会话并运行它：
sess = tf.compat.v1.Session()
print(sess.run(c))
结果：
20
总之，记住要初始化变量，创建会话并在会话中运行操作
接下来，我们需要了解一下占位符（placeholders）。占位符是一个对象，它的值只能在稍后指定，要指定占位符的值，可以使用一个feed字典（feed_dict变量）来传入，接下来，我们为x创建一个占位符，这将允许我们在稍后运行会话时传入一个数字。
x = tf.compat.v1.placeholder(tf.int64, name = 'x')
print(sess.run(2 * x, feed_dict = {x: 3}))
sess.close()
结果：
6
当你第一次定义x时，你不需要为它指定一个值。占位符只是一个变量，您只会在以后运行会话时将数据分配给它。我们说，在运行会话时将数据提供给这些占位符。
事情是这样的:当你指定一个计算所需的操作时，你就是在告诉TensorFlow如何构造一个计算图。计算图可以有一些占位符，稍后您将指定其值。最后，当您运行会话时，您正在告诉TensorFlow执行计算图。
线性函数
通过计算下面的等式开始这个编程练习:=+,在那里和都是随机矩阵，b是随机向量。
计算+，,,都是从随机正态分布中得出的。W的形状为(4,3)，X为(3,1)，b为(4,1)。举个例子，下面是你如何定义一个形状为(3,1)的常量X:
X = tf.constant(np.random.randn(3,1), name = “X”)
def linear_function():
np.random.seed(1)
W = tf.constant(np.random.randn(4,3), name = "W")
X = tf.constant(np.random.randn(3,1), name = "X")
b = tf.constant(np.random.randn(4,1), name = "b")
y = tf.add(tf.matmul(W,X),b)
sess = tf.compat.v1.Session()
result = sess.run(y)
sess.close()
return result
结果：
result = [[-1.98748544]
[-2.76826248]
[-0.78635415]
[-2.77463846]]
sigmoid函数
实现了线性函数，TensorFlow提供了多种常用的神经网络的函数比如tf.softmax和 tf.sigmoid。使用占位符变量x，当运行这个session的时候，我们需要使用使用feed字典来输入z，我们将创建占位符变量x，使用tf.sigmoid来定义操作符，最后运行session，我们会用到下面的代码：
- tf.placeholder(tf.float32, name = “…”)
- tf.sigmoid(…)
- sess.run(…, feed_dict = {x: z})
可以使用两种方法来创建并使用session
sess = tf.Session()
result = sess.run(..., feed_dict = {...})
sess.close()
with tf.Session() as sess:
result = sess.run(..., feed_dict = {...})
def sigmoid(z):
x = tf.compat.v1.placeholder(tf.float32, name = 'x')
sigmoid = tf.sigmoid(x)
sess = tf.compat.v1.Session()
result = sess.run(sigmoid, feed_dict = {x:z})
sess.close()
#可替换为：
#with tf.Session() as sess:
# result = sess.run(sigmoid, feed_dict = {x:z})
return result
测试：
print ("sigmoid(0) = " + str(sigmoid(0)))
print ("sigmoid(12) = " + str(sigmoid(12)))
结果：
sigmoid(0) = 0.5
sigmoid(12) = 0.99999386
损失函数
可以使用内置函数计算神经网络的成本。因此，不需要编写代码来计算成本函数的a[2](i)和yi
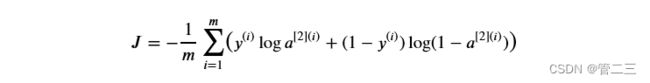
可以在tensorflow中的一行代码中完成它!
tf.nn.sigmoid_cross_entropy_with_logits(logits = …, labels = …)
你的代码应该输入z，计算sigmoid（得到 a），然后计算交叉熵成本J ，所有的步骤都可以通过一次调用上述代码实现。
def cost(logits, labels):
z = tf.compat.v1.placeholder(tf.float32, name = 'z')
y = tf.compat.v1.placeholder(tf.float32, name = 'y')
loss = tf.nn.sigmoid_cross_entropy_with_logits(logits=z, labels=y)
sess = tf.compat.v1.Session()
cost = sess.run(loss,feed_dict = {z:logits,y:labels})
sess.close()
return cost
测试：
logits = sigmoid(np.array([0.2,0.4,0.7,0.9]))
cost = cost(logits, np.array([0,0,1,1]))
print ("cost = " + str(cost))
结果：
cost = [1.0053873 1.0366408 0.41385433 0.39956617]
独热编码（0、1编码）
在深度学习中，很多时候你会得到一个y向量，其中的数字从0到C-1，其中C是类的数量。如果C为例4，那么你可能有以下的y向量，你需要转换如下:
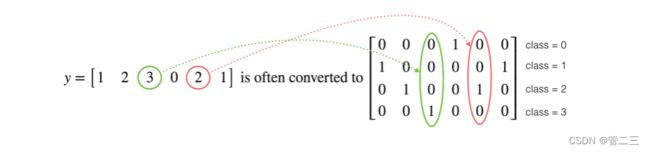这被称为“one hot”编码，因为在转换后的表示中，每列中只有一个元素是“hot”(意味着设置为1)。要在numpy中进行这种转换，可能需要编写几行代码。在tensorflow中，你可以使用一行代码:
tf.one_hot(labels, depth, axis)
实现下面的函数，取标签的一个向量和类C的总数，并返回一个热编码。
def one_hot_matrix(labels, C):
C = tf.constant(C,name = "C")
hot = tf.one_hot(labels,C,axis=0)
sess = tf.compat.v1.Session()
one_hot = sess.run(hot)
sess.close()
return one_hot
axis = 0按列，1按行
测试：
labels = np.array([1,2,3,0,2,1])
one_hot = one_hot_matrix(labels, C = 4)
print ("one_hot = " + str(one_hot))
结果：
one_hot = [[0. 0. 0. 1. 0. 0.]
[1. 0. 0. 0. 0. 1.]
[0. 1. 0. 0. 1. 0.]
[0. 0. 1. 0. 0. 0.]]
初始化为0和1
现在我们将学习如何用0或者1初始化一个向量，我们要用到tf.ones()和tf.zeros()，给定这些函数一个维度值那么它们将会返回全是1或0的满足条件的向量/矩阵。
def ones(shape):
ones = tf.ones(shape)
sess = tf.compat.v1.Session()
ones = sess.run(ones)
sess.close()
return ones
测试：
print ("ones = " + str(ones([3])))
结果：
ones = [1. 1. 1.]
使用TensorFlow构建你的第一个神经网络
实现TensorFlow模型有两部分:
- 创建计算图
- 运行计算图
建立一个手语识别模型，数据集如下：
训练集：有从0到5的数字的1080张图片(64x64像素)，每个数字拥有180张图片。
测试集：有从0到5的数字的120张图片(64x64像素)，每个数字拥有5张图片。
下面是每个数字的样本，以及我们如何表示标签的解释。这些都是原始图片，我们实际上用的是64 * 64像素的图片。
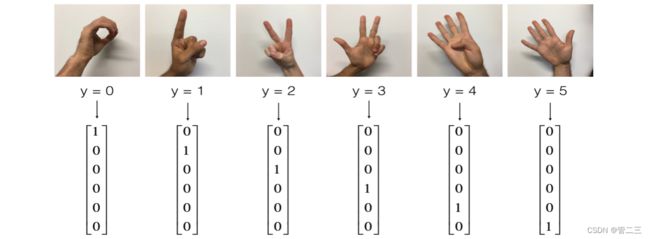
加载数据集
X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = load_dataset()
数据集归一化，标签转化为独热向量
# 每一列就是一个例子
X_train_flatten = X_train_orig.reshape(X_train_orig.shape[0], -1).T
X_test_flatten = X_test_orig.reshape(X_test_orig.shape[0], -1).T
# 归一化
X_train = X_train_flatten/255.
X_test = X_test_flatten/255.
# y转化为独热矩阵
Y_train = convert_to_one_hot(Y_train_orig, 6)
Y_test = convert_to_one_hot(Y_test_orig, 6)
目标是建立一个能够高精度识别符号的算法。为此，您将构建一个TensorFlow模型，它与您之前在numpy中为cat识别构建的模型几乎相同(但现在使用softmax输出)。这是一个比较numpy实现和tensorflow实现的好机会。
目前的模型是：LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SOFTMAX，SIGMOID输出层已经转换为SOFTMAX。当有两个以上的类时，一个SOFTMAX层将SIGMOID一般化。
创建placeholders
为x，y创建占位符
def create_placeholders(n_x, n_y):
X = tf.compat.v1.placeholder(tf.float32,[n_x, None],name="X")
Y = tf.compat.v1.placeholder(tf.float32,[n_y, None],name="Y")
return X, Y
测试：
X, Y = create_placeholders(12288, 6)
print ("X = " + str(X))
print ("Y = " + str(Y))
结果：
X = Tensor("X_27:0", shape=(12288, None), dtype=float32)
Y = Tensor("Y_5:0", shape=(12288, None), dtype=float32)
初始化参数
实现下面的函数来初始化tensorflow中的参数。您将使用Xavier初始化表示权重，使用Zero初始化表示偏差。这些形状如下所示。举个例子，为了帮助你，对于W1和b1你可以使用:
W1 = tf.get_variable(“W1”, [25,12288], initializer = tf.contrib.layers.xavier_initializer(seed = 1))
b1 = tf.get_variable(“b1”, [25,1], initializer = tf.zeros_initializer())
def initialize_parameters():
tf.compat.v1.set_random_seed(1)
W1 = tf.compat.v1.get_variable("W1",[25, 12288],initializer = tf.keras.initializers.glorot_normal(seed = 1))
b1 = tf.compat.v1.get_variable("b1", [25,1], initializer = tf.zeros_initializer())
W2 = tf.compat.v1.get_variable("W2",[12, 25],initializer = tf.keras.initializers.glorot_normal(seed = 1))
b2 = tf.compat.v1.get_variable("b2", [12, 1], initializer = tf.zeros_initializer())
W3 = tf.compat.v1.get_variable("W3",[6, 12],initializer = tf.keras.initializers.glorot_normal(seed = 1))
b3 = tf.compat.v1.get_variable("b3", [6, 1], initializer = tf.zeros_initializer())
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2,
"W3": W3,
"b3": b3}
return parameters
如果是tf2的版本，contrib已经被舍弃了，可以将tf.contrib.layers.xavier_initializer更换为tf.keras.initializers.glorot_normal，编译器相关算法完全相同
测试：
tf.compat.v1.reset_default_graph()
with tf.compat.v1.Session() as sess:
parameters = initialize_parameters()
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
结果：
W1 = <tf.Variable 'W1:0' shape=(25, 12288) dtype=float32>
b1 = <tf.Variable 'b1:0' shape=(25, 1) dtype=float32>
W2 = <tf.Variable 'W2:0' shape=(12, 25) dtype=float32>
b2 = <tf.Variable 'b2:0' shape=(12, 1) dtype=float32>
前向传播
我们将要在TensorFlow中实现前向传播，该函数将接受一个字典参数并完成前向传播。
def forward_propagation(X, parameters):
W1 = parameters['W1']
b1 = parameters['b1']
W2 = parameters['W2']
b2 = parameters['b2']
W3 = parameters['W3']
b3 = parameters['b3']
Z1 = tf.add(tf.matmul(W1,X),b1)
a1 = tf.nn.relu(Z1)
Z2 = tf.add(tf.matmul(W2,a1),b2)
a2 = tf.nn.relu(Z2)
Z3 = tf.add(tf.matmul(W3,a2),b3)
return Z3
测试：
tf.compat.v1.reset_default_graph()
with tf.compat.v1.Session() as sess:
X, Y = create_placeholders(12288, 6)
parameters = initialize_parameters()
Z3 = forward_propagation(X, parameters)
print("Z3 = " + str(Z3))
结果：
Z3 = Tensor("Add_2:0", shape=(6, None), dtype=float32)
损失函数
如前所述，成本很容易计算：
tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits = …, labels = …))
def compute_cost(Z3, Y):
logits = tf.transpose(Z3)
labels = tf.transpose(Y)
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits = logits, labels = labels))
return cost
测试：
tf.compat.v1.reset_default_graph()
with tf.compat.v1.Session() as sess:
X, Y = create_placeholders(12288, 6)
parameters = initialize_parameters()
Z3 = forward_propagation(X, parameters)
cost = compute_cost(Z3, Y)
print("cost = " + str(cost))
结果：
cost = Tensor("Mean:0", shape=(), dtype=float32)
反向传播与参数更新
得益于编程框架，所有反向传播和参数更新都在1行代码中处理。计算成本函数后，将创建一个“optimizer”对象。 运行tf.session时，必须将此对象与成本函数一起调用，当被调用时，它将使用所选择的方法和学习速率对给定成本进行优化。
对于梯度下降：
optimizer = tf.train.GradientDescentOptimizer(learning_rate = learning_rate).minimize(cost)
优化：
_ , c = sess.run([optimizer, cost], feed_dict={X: minibatch_X, Y: minibatch_Y})
_ 作为一次性变量来存储我们稍后不需要使用的值。
构建模型
def model(X_train, Y_train, X_test, Y_test, learning_rate = 0.0001,
num_epochs = 1500, minibatch_size = 32, print_cost = True):
ops.reset_default_graph() # to be able to rerun the model without overwriting tf variables
tf.compat.v1.set_random_seed(1) # to keep consistent results
seed = 3 # to keep consistent results
(n_x, m) = X_train.shape # (n_x: input size, m : number of examples in the train set)
n_y = Y_train.shape[0] # n_y : output size
costs = [] # To keep track of the cost
X, Y = create_placeholders(n_x, n_y)
parameters = initialize_parameters()
Z3 = forward_propagation(X, parameters)
cost = compute_cost(Z3, Y)
optimizer = tf.compat.v1.train.GradientDescentOptimizer(learning_rate = learning_rate).minimize(cost)
init = tf.compat.v1.global_variables_initializer()
with tf.compat.v1.Session() as sess:
sess.run(init)
for epoch in range(num_epochs):
epoch_cost = 0. # Defines a cost related to an epoch
num_minibatches = int(m / minibatch_size) # number of minibatches of size minibatch_size in the train set
seed = seed + 1
minibatches = random_mini_batches(X_train, Y_train, minibatch_size, seed)
for minibatch in minibatches:
(minibatch_X, minibatch_Y) = minibatch
_ , minibatch_cost = sess.run([optimizer, cost], feed_dict={X: minibatch_X, Y: minibatch_Y})
epoch_cost += minibatch_cost / num_minibatches
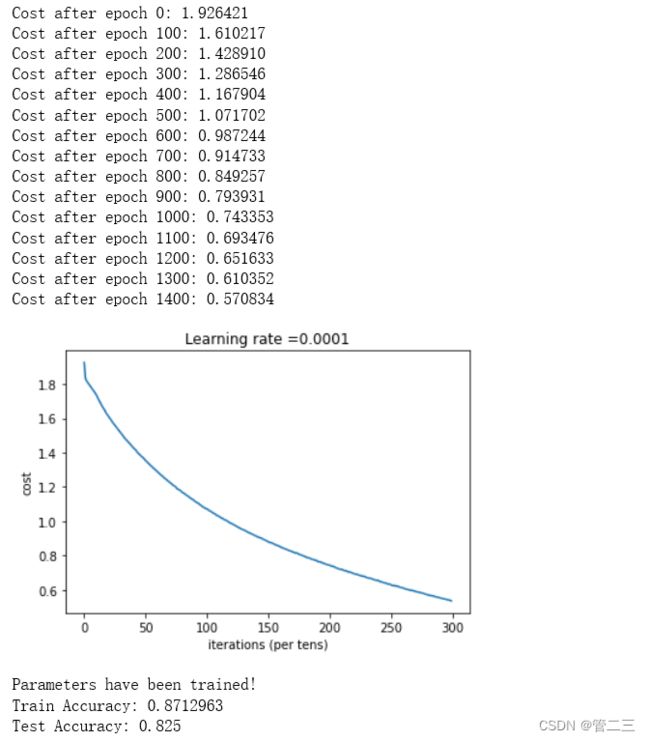
if print_cost == True and epoch % 100 == 0:
print ("Cost after epoch %i: %f" % (epoch, epoch_cost))
if print_cost == True and epoch % 5 == 0:
costs.append(epoch_cost)
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
parameters = sess.run(parameters)
print ("Parameters have been trained!")
correct_prediction = tf.equal(tf.argmax(Z3), tf.argmax(Y))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
print ("Train Accuracy:", accuracy.eval({X: X_train, Y: Y_train}))
print ("Test Accuracy:", accuracy.eval({X: X_test, Y: Y_test}))
return parameters
运行：
parameters = model(X_train, Y_train, X_test, Y_test)
结果：
