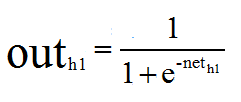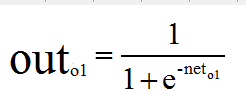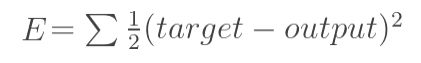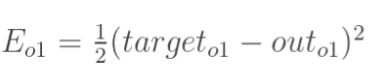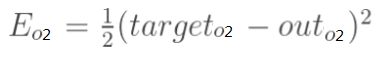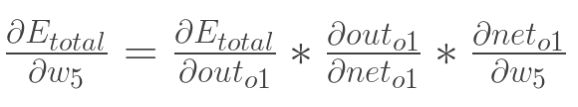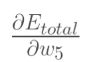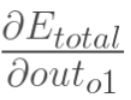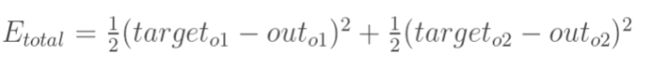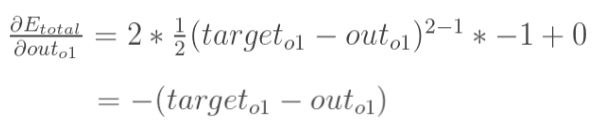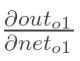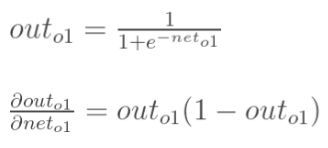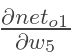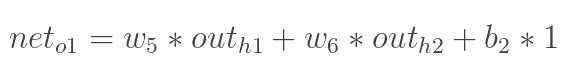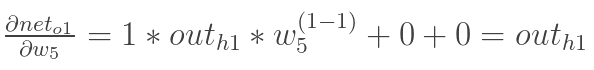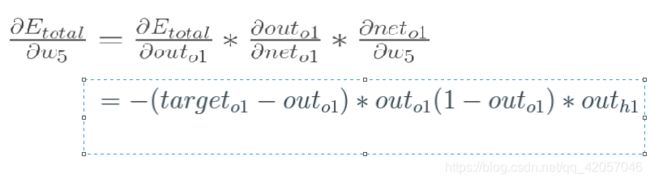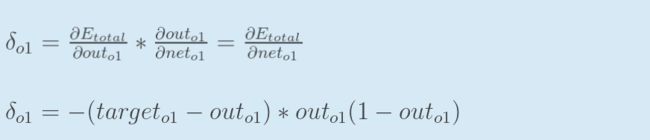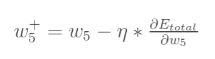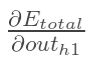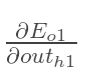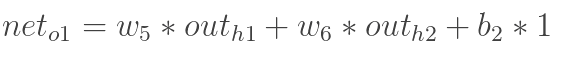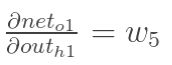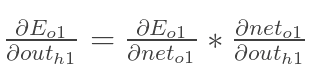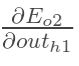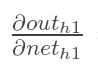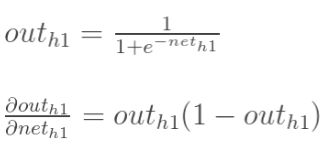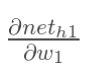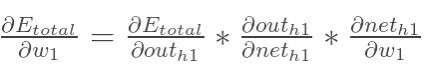BP神经网络-神经网络前向传播和反向(BP)传播及其python实现

前言

BP神经网络，可以理解为使用“BP算法进行训练”的“多层感知器模型”

多层感知器（MLP）就是指得结构上多层的感知器模型递接连成的前向型网络。BP就是指得反向传播算法

MLP这个术语属于历史遗留的产物，现在我们一般就说神经网络，

而感知感知器是生物神经细胞的简单抽象，我们可以理解为神经网络中的一个神经元

 

---

BP神经网络（BackPropagation Neuron NetWok）

首先在这里现阐述一下深度神经网络和BP神经网络的关系

我们在学习神经网络过程中，经常会被DNN（深度神经网络），BPNN，CNN，DBN等搞的晕头转向，我个人理解的是，DNN（深度神经网络），BPNN，CNN，DBN都是人工神经网络的延伸，深度神经网络是一个较为抽象的概念属于神经网络中一个大类，理论上说拥有两层及以上的隐含层的神经网络都可以看作是深度神经网络，而cnn，DBN都可以看作是对深度神经网络中的一个范畴。

bp神经网络学习算法可以说是目前最成功的神经网络学习算法。显示任务中使用神经网络时，大多数是使用BP算法进行训练. 

BP神经网络其实就是一个”万能的模型+误差修正函数“，每次根据训练得到的结果与预想结果进行误差分析，进而修改权值和阈值，一步一步得到能输出和预想结果一致的模型

BP算法的基本思想是：学习过程由信号的正向传播和误差的反向传播俩个过程组成，输入从输入层输入，经隐层处理以后，传向输出层。如果输出层的实际输出和期望输出不符合，就进入误差的反向传播阶段。误差反向传播是将输出误差以某种形式通过隐层向输入层反向传播，并将误差分摊给各层的所有单元，从而获得各层单元的误差信号，这个误差信号就作为修正个单元权值的依据。知道输出的误差满足一定条件或者迭代次数达到一定次数。

---

神经网络基本结构

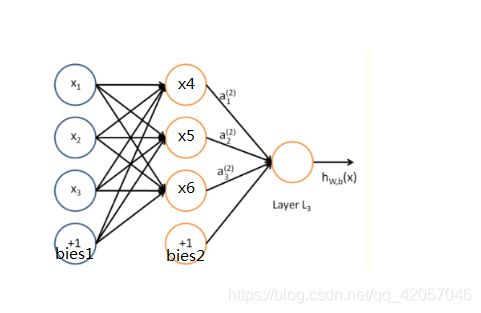
下面是一个很典型的三层神经网络的基本组结构
 

层：神经网络是一个分层 (Layer) 结构，一般的神经网络都由输入层 (Input Layer) 、隐藏层 (Hidden Layer)、输出层 (Output Layer)所组成。其中隐藏层的数量根据所构建的神经网络的复杂程度可以从零达到几百层。

节点：神经网络中的每一层都是由若干个节点 (Node) 所组成。我们可以把节点理解为对数据处理的单元，每个节点的作用就是接收所有传入的数值，经过计算处理后输出一个数值。同一层的所有节点的输出值组合起来就是一个 N×1  维的向量，N 为该层中节点的个数。特别的是，第 输入层中的每个节点对输入的数值不做任何处理直接输出，也可以把输入层当作数据本身。比如最常见的图像数据，如果彩色图像数据像素为 64×64 ，考虑到其中的三个颜色通道，那么向量化输入的数据应该是长度为 64×64×3=12288 的列向量。

连接：同一层之间的节点没有连接，非相邻层之间的节点也没有连接，相邻层之间的任意两个节点之间都有连接。通过这种连接使得一层中的节点存储的值传递到下一层中的各个节点。需要注意的是，数据在从一层传递到下一层的过程中是经过了加权的。

其中那个LayerL1是这个三层神经网络的输入层，LayerL2是这个神经网络的的隐含层，LayerL3是输出层，x1,x2,x3为输入层的节点，bies1为输入层的偏执项（偏置量的作用是给网络分类增加平移的能力。具体见https://www.jiqizhixin.com/articles/2018-07-05-18），x4，x5,x6,为隐含层节点，bies2为隐含层的偏执项，目前我们手上有一对数据｛x1,x2,x3,.....xn｝输入，输出也是一堆数据｛y1,y2,y3,......yn｝，我们现在将要做的是，在隐含层做某种变换，当我们将数据数进去的时候，能够得到我们期望的输出。

---

神经网络的学习方法

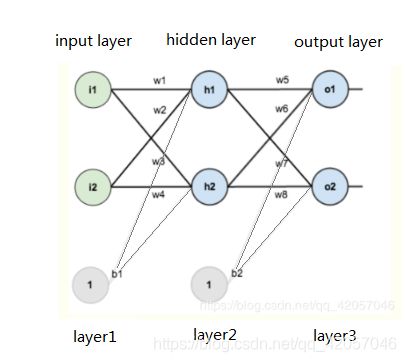
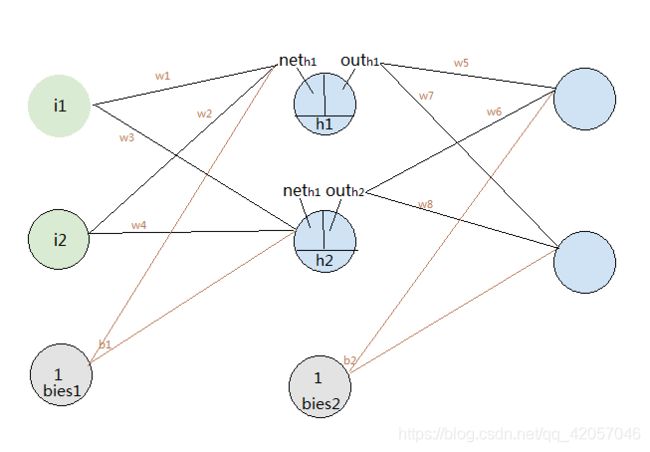
如下图所示，是一个简单的神经网络：

上图中的神经网络可分为三层

       第一层是输入层，包含两个神经元i1，i2，和偏执节点或（截距项）b1；

       第二层是隐含层，包含两个神经元h1,h2和偏执节点或（截距项）b2；

       第三层是输出层，输出o1,o2，

       层与层之间每条线上标的wi代表层与层之间连接的权重；

       激活函数我们可以使用sigmoid函数也可以使用Tanh函数或ReLU函数。

       关于激活函数的详解可参考： https://blog.csdn.net/qq_42057046/article/details/96487113

---

我们以下图所给这个神经为例

如图所示：

       输入数据为i1，i2

       原输出数据为o1，o2

       输入层到隐含层的权重为w1，w2，w3，w4

       隐含层到输出层的权重为w5，w6，w7，w8

       我们现在的目标是：给出输入数据i1，i2是计算得到的输出o1‘，o2‘尽可能的与原始数据o1，o2接近。

大致可分为两步，神经网路的前向传播，反向传播

---

一，神经网络的向前传播

神经网络有反向传播，那肯定就有神经网络的前向传播啦，我们在这里首先先提一下神经网络的前向传播过程，这部分很容易理解。神经网络的前向传播的目的就是网络如何根据输入X得到输出Y，这个很容易理解，以我们所给的图为例，神经网络的前向传播可分为输入层到隐含层的传播和隐含层到输出层的传播，如神经网络有多个隐含层，还会有隐含层到隐含层之间的传播，但层与层之间传播的规律是相同的。具体如下：

1.输入层——隐含层：

我们首先要根据所给的输入值，计算h1的加权和：

 神经元h1的输出o1：（这里激活函数以sigmoid函数为例，关于激活函数可以看我的另一篇博客：                                   https://blog.csdn.net/qq_42057046/article/details/96487113）：   

同理可以计算出神经元h2的加权和的输出outh2（neth2和outh2）

2.隐含层——输出层：

计算输出神经元o1和o2的加权值和输出值：

 

同理可以得到net02，outo2的值

以上便我们所给的三层神经网络的前向传播过程，过程十分简单，整个前向传播的过程都是从输入层开始的，中间层的节点求得的加权值不能直接作为输出进入到下一个节点的运算，而是需要经过激活函数的处理后，生成相应的输出out进入到下层，在最后的输出层也不例外。

 

---

 

二，误差信号反向传播

首先误差信号反向传播首先经过输出层，所以我们首先调整隐含层和输出层之间的权值。然后在向前调整输出层和隐含层之间权值。

在调整权值的阶段，沿着网络逐层反向进行调整。具体过程如下：

当神经网络输出与期望输出不等时，会存在输出误差E（即误差函数loss）：

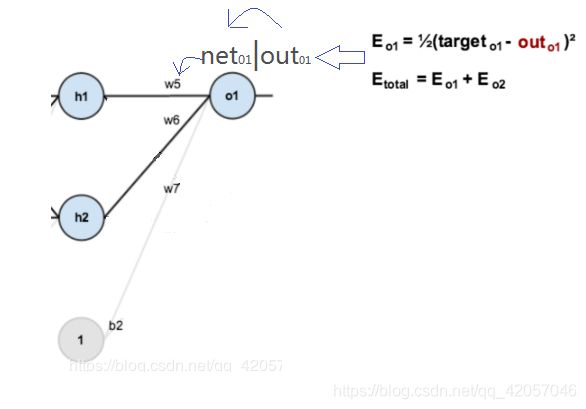
以我所给的神经网络结构为例

误差E可以看作o1和o2误差之和，我们可以分别计算o1，o2的误差，便可以得到总误差，o1，o2的误差如下：

误差信号的反向传播有输出层向前调整，进而更新层与层之间的权值。

1.隐含层——输出层之间的权值更新

在这里，我们以w5为例，我们想要对权值w5进行更新，首先我们要知道w5对整体误差产生了多少影响，这个影响我们可以用整体误差对W5求偏导得出。对于整体误差对w5的偏导数，我们又可以得出如下公式。

现在我们以w5为例计算中每一个式子的值：

1.计算  

2.计算  

3.计算 

4.根据以上的式子计算  

通过上面求解每一个式子最终我们可以求的总误差对w5的偏导数，同理我们可以求得隐含层到输出层的总误差对其他权值的偏导数

为方便表达，我们现在用 表示输出层误差

因此，整体误差E(total)对w5的偏导公式可以写成：

如果输出层误差计为负的话，也可以写成：

最后我们来更新w5的值：

（其中，是学习速率）

 

同理我们可以求得与w5同一层次的  等等......

 

上面我们讲解了隐含层到输出层的误差反向传播和权值更新。下面我们将着眼于输入层到隐含层

 

---

1.输入层——输出层隐含层之间的权值更新

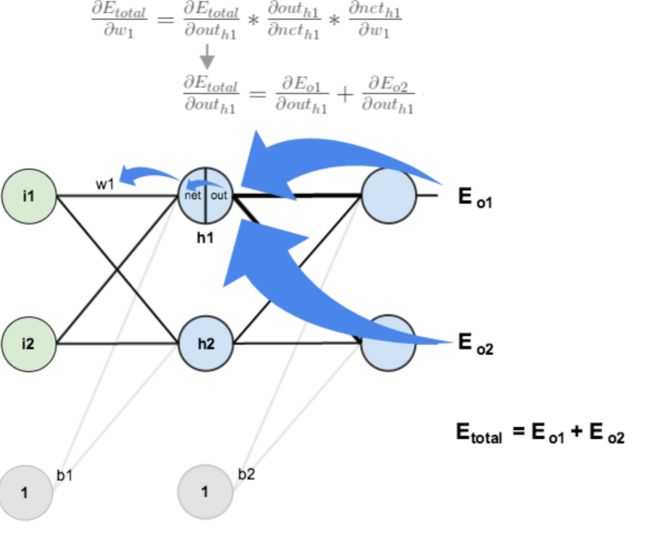
方法其实与上面说的差不多，但是有个地方需要变一下，在上文计算总误差对w5的偏导时，是从out(o1)---->net(o1)---->w5,但是在隐含层之间的权值更新时，是out(h1)---->net(h1)---->w1,而out(h1)会接受E(o1)和E(o2)两个地方传来的误差，所以这个地方两个都要计算。

 

 

计算：

                       

先计算：

                               

                               

                              

                                

同理，计算出：

　　　　　　　　

两者相加得到总值：

                                

再计算：

                               

再计算：

                              

最后，三者相乘：

                                

 为了简化公式，用sigma(h1)表示隐含层单元h1的误差：  

最后，更新w1的权值：

同理，额可更新w2,w3,w4的权值：

 

　　这样误差反向传播法就完成了，最后我们再把更新的权值重新计算，不停地迭代，直到最终的出结果

 

 

 

代码：下面给的第一个代码，是我自己找的一篇，我在原有代码的基础上进行了少量的修改，详细的注释。第二个代码，较第一个来书要难，涉及python中类这一部分知识较深，自己做参考。

import numpy as np
import random
import matplotlib.pyplot as plt
 
#random.seed(0)  #当我们设置相同的seed，每次生成的随机数相同。如果不设置seed，则每次会生成不同的随机数
                #参考https://blog.csdn.net/jiangjiang_jian/article/details/79031788
 
#生成区间[a,b]内的随机数
def random_number(a,b):
    #python自带random用于生成随机数，numpy中的random用于生成随机数矩阵,random()生成0到1之间的数
    return (b-a)*random.random()+a 
 
#生成一个矩阵，大小为m*n,并且设置默认零矩阵
def makematrix(m, n, fill=0.0):
    a = []
    for i in range(m):
        a.append([fill]*n) #[X]*n得到的结果是一个n元数组,例如[0.0]*3结果为[0.0 0.0 0.0]
    return a
 
#函数sigmoid(),这里采用tanh，因为看起来要比标准的sigmoid函数好看
def sigmoid(x):
    return np.tanh(x) #1/(1+np.exp(-x))
 
#函数sigmoid的派生函数
def derived_sigmoid(x):
    return 1.0 - x**2  #** 代表乘方，这里的1-tanh(x)^2是tanh(x)的导数
 
#构造三层BP网络架构
class BPNN:
    def __init__(self, num_in, num_hidden, num_out):
        #输入层，隐藏层，输出层的节点数
        self.num_in = num_in + 1  #增加一个偏置结点bies
        self.num_hidden = num_hidden + 1   #增加一个偏置结点bies
        self.num_out = num_out
        
        #激活神经网络的所有节点（向量）
        #由于偏执节点值一般都为1，所以创建节点初始值默认为一
        self.active_in = [1.0]*self.num_in #创建输入层节点
        self.active_hidden = [1.0]*self.num_hidden #创建隐含层节点
        self.active_out = [1.0]*self.num_out #创建输出曾节点
        
        #创建权重矩阵
        self.wight_in = makematrix(self.num_in, self.num_hidden) #输入层到隐含层的权重矩阵
        self.wight_out = makematrix(self.num_hidden, self.num_out) #隐含层到输出层的权重矩阵
        
        #对输入层到隐含层的权值矩阵赋初值
        for i in range(self.num_in):
            for j in range(self.num_hidden):
                self.wight_in[i][j] = random_number(-0.2, 0.2)
        #对隐含层到输出层的权重矩阵赋初值      
        for i in range(self.num_hidden):
            for j in range(self.num_out):
                self.wight_out[i][j] = random_number(-0.2, 0.2)
    
        #最后建立动量因子（矩阵）
        self.ci = makematrix(self.num_in, self.num_hidden)
        self.co = makematrix(self.num_hidden, self.num_out)        
        
    #信号正向传播
    def update(self, inputs):
        if len(inputs) != self.num_in-1:
            raise ValueError('与输入层节点数不符')
            
        #将输入数据同步到输入层，输入层有一个数据是偏执节点dies
        for i in range(self.num_in - 1):
            #self.active_in[i] = sigmoid(inputs[i])  #或者先在输入层进行数据处理
            self.active_in[i] = inputs[i]  #active_in[]是输入数据的矩阵
            
        #数据在隐藏层的处理
        for i in range(self.num_hidden - 1): #i代表隐含层节点序号
            sum = 0.0
            for j in range(self.num_in): #j代表输入层节点序号
                sum = sum + self.active_in[i] * self.wight_in[j][i]
            self.active_hidden[i] = sigmoid(sum)   #active_hidden[]是处理完输入数据之后存储，作为输出层的输入数据
            
        #数据在输出层的处理
        for i in range(self.num_out): #i代表输出层节点序号
            sum = 0.0
            for j in range(self.num_hidden): #j代表隐含层节点序号
                sum = sum + self.active_hidden[j]*self.wight_out[j][i]
            self.active_out[i] = sigmoid(sum)   #与上同理
            
        return self.active_out[:]
    
    #误差反向传播
    def errorbackpropagate(self, targets, lr, m):   #lr是学习率， m是动量因子，用于防止局部最优
        if len(targets) != self.num_out:
            raise ValueError('与输出层节点数不符！')
            
        #首先计算输出层的误差 
        out_deltas = [0.0]*self.num_out
        for i in range(self.num_out):
            error = targets[i] - self.active_out[i]
            out_deltas[i] = derived_sigmoid(self.active_out[i])*error #derived_sigmoid()函数返回 1.0 - x**2
        
        #然后计算隐藏层误差
        hidden_deltas = [0.0]*self.num_hidden
        for i in range(self.num_hidden):
            error = 0.0
            for j in range(self.num_out):
                error = error + out_deltas[j]* self.wight_out[i][j]
            hidden_deltas[i] = derived_sigmoid(self.active_hidden[i])*error
        
        #首先更新输出层权值
        for i in range(self.num_hidden):
            for j in range(self.num_out):
                change = out_deltas[j]*self.active_hidden[i]
                self.wight_out[i][j] = self.wight_out[i][j] + lr*change + m*self.co[i][j]
                self.co[i][j] = change
                
        #然后更新输入层权值
        for i in range(self.num_in):
            for i in range(self.num_hidden):
                change = hidden_deltas[j]*self.active_in[i]
                self.wight_in[i][j] = self.wight_in[i][j] + lr*change + m* self.ci[i][j]
                self.ci[i][j] = change
                
        #计算总误差
        error = 0.0
        for i in range(len(targets)):
            error = error + 0.5*(targets[i] - self.active_out[i])**2
        return error
 
    #测试
    def test(self, patterns):
        for i in patterns:
            print(i[0], '->', self.update(i[0]))
    #权重
    def weights(self):
        print("输入层权重")
        for i in range(self.num_in):
            print(self.wight_in[i])
        print("输出层权重")
        for i in range(self.num_hidden):
            print(self.wight_out[i])
            
    def train(self, pattern, itera=100000, lr = 0.1, m=0.1):
        for i in range(itera):
            error = 0.0
            for j in pattern:
                inputs = j[0]
                targets = j[1]
                self.update(inputs)
                error = error + self.errorbackpropagate(targets, lr, m)
            if i % 100 == 0:
                print('误差 %-.5f' % error)
    
#实例
def demo():
    patt = [
            [[1,2,5],[0]],
            [[1,3,4],[1]],
            [[1,6,2],[1]],
            [[1,5,1],[0]],
            [[1,8,4],[1]]
            ]
    #创建神经网络，3个输入节点，3个隐藏层节点，1个输出层节点
    n = BPNN(3, 3, 1)
    #训练神经网络
    n.train(patt)
    #测试神经网络
    n.test(patt)
    #查阅权重值
    n.weights()
 
     
if __name__ == '__main__':
    demo()
 

 

---

代码二：

#coding:utf-8
import random
import math

#
#   参数解释：
#   "pd_" ：偏导的前缀
#   "d_" ：导数的前缀
#   "w_ho" ：隐含层到输出层的权重系数索引
#   "w_ih" ：输入层到隐含层的权重系数的索引

class NeuralNetwork:
    LEARNING_RATE = 0.5

    #__init__详解见 https://blog.csdn.net/geerniya/article/details/77487941
    #类中函数的第一个参数self指的是类实例对象本身(注意：不是类本身)。
    def __init__(self, num_inputs, num_hidden, num_outputs, hidden_layer_weights = None, hidden_layer_bias = None, output_layer_weights = None, output_layer_bias = None):
        
        self.num_inputs = num_inputs#输入层数据量

        self.hidden_layer = NeuronLayer(num_hidden, hidden_layer_bias)#隐藏层
        self.output_layer = NeuronLayer(num_outputs, output_layer_bias)#输出层

        self.init_weights_from_inputs_to_hidden_layer_neurons(hidden_layer_weights)
        self.init_weights_from_hidden_layer_neurons_to_output_layer_neurons(output_layer_weights)

    def init_weights_from_inputs_to_hidden_layer_neurons(self, hidden_layer_weights):
        weight_num = 0
        for h in range(len(self.hidden_layer.neurons)):
            for i in range(self.num_inputs):
                if not hidden_layer_weights:
                    self.hidden_layer.neurons[h].weights.append(random.random())
                else:
                    self.hidden_layer.neurons[h].weights.append(hidden_layer_weights[weight_num])
                weight_num += 1

    def init_weights_from_hidden_layer_neurons_to_output_layer_neurons(self, output_layer_weights):
        weight_num = 0
        for o in range(len(self.output_layer.neurons)):
            for h in range(len(self.hidden_layer.neurons)):
                if not output_layer_weights:
                    self.output_layer.neurons[o].weights.append(random.random())
                else:
                    self.output_layer.neurons[o].weights.append(output_layer_weights[weight_num])
                weight_num += 1


    def inspect(self):
        print('------')
        print('* Inputs: {}'.format(self.num_inputs))
        print('------')
        print('Hidden Layer')
        self.hidden_layer.inspect()
        print('------')
        print('* Output Layer')
        self.output_layer.inspect()
        print('------')

    def feed_forward(self, inputs):
        hidden_layer_outputs = self.hidden_layer.feed_forward(inputs)
        return self.output_layer.feed_forward(hidden_layer_outputs)

    def train(self, training_inputs, training_outputs):
        self.feed_forward(training_inputs)

        # 1. 输出神经元的值
        pd_errors_wrt_output_neuron_total_net_input = [0] * len(self.output_layer.neurons)
        for o in range(len(self.output_layer.neurons)):

            # ∂E/∂zⱼ
            pd_errors_wrt_output_neuron_total_net_input[o] = self.output_layer.neurons[o].calculate_pd_error_wrt_total_net_input(training_outputs[o])

        # 2. 隐含层神经元的值
        pd_errors_wrt_hidden_neuron_total_net_input = [0] * len(self.hidden_layer.neurons)
        for h in range(len(self.hidden_layer.neurons)):

            # dE/dyⱼ = Σ ∂E/∂zⱼ * ∂z/∂yⱼ = Σ ∂E/∂zⱼ * wᵢⱼ
            d_error_wrt_hidden_neuron_output = 0
            for o in range(len(self.output_layer.neurons)):
                d_error_wrt_hidden_neuron_output += pd_errors_wrt_output_neuron_total_net_input[o] * self.output_layer.neurons[o].weights[h]

            # ∂E/∂zⱼ = dE/dyⱼ * ∂zⱼ/∂
            pd_errors_wrt_hidden_neuron_total_net_input[h] = d_error_wrt_hidden_neuron_output * self.hidden_layer.neurons[h].calculate_pd_total_net_input_wrt_input()

        # 3. 更新输出层权重系数
        for o in range(len(self.output_layer.neurons)):
            for w_ho in range(len(self.output_layer.neurons[o].weights)):

                # ∂Eⱼ/∂wᵢⱼ = ∂E/∂zⱼ * ∂zⱼ/∂wᵢⱼ
                pd_error_wrt_weight = pd_errors_wrt_output_neuron_total_net_input[o] * self.output_layer.neurons[o].calculate_pd_total_net_input_wrt_weight(w_ho)

                # Δw = α * ∂Eⱼ/∂wᵢ
                self.output_layer.neurons[o].weights[w_ho] -= self.LEARNING_RATE * pd_error_wrt_weight

        # 4. 更新隐含层的权重系数
        for h in range(len(self.hidden_layer.neurons)):
            for w_ih in range(len(self.hidden_layer.neurons[h].weights)):

                # ∂Eⱼ/∂wᵢ = ∂E/∂zⱼ * ∂zⱼ/∂wᵢ
                pd_error_wrt_weight = pd_errors_wrt_hidden_neuron_total_net_input[h] * self.hidden_layer.neurons[h].calculate_pd_total_net_input_wrt_weight(w_ih)

                # Δw = α * ∂Eⱼ/∂wᵢ
                self.hidden_layer.neurons[h].weights[w_ih] -= self.LEARNING_RATE * pd_error_wrt_weight

    def calculate_total_error(self, training_sets):
        total_error = 0
        for t in range(len(training_sets)):
            training_inputs, training_outputs = training_sets[t]
            self.feed_forward(training_inputs)
            for o in range(len(training_outputs)):
                total_error += self.output_layer.neurons[o].calculate_error(training_outputs[o])
        return total_error



class NeuronLayer:
    def __init__(self, num_neurons, bias):
        #num_neurons：相应层原点数

        # 同一层的神经元共享一个截距项b
        self.bias = bias if bias else random.random()

        self.neurons = []
        for i in range(num_neurons):
            self.neurons.append(Neuron(self.bias))

    def inspect(self):
        print('Neurons:', len(self.neurons))
        for n in range(len(self.neurons)):
            print(' Neuron', n)
            for w in range(len(self.neurons[n].weights)):
                print('  Weight:', self.neurons[n].weights[w])
            print('  Bias:', self.bias)

    def feed_forward(self, inputs):
        outputs = []
        for neuron in self.neurons:
            outputs.append(neuron.calculate_output(inputs))
        return outputs

    def get_outputs(self):
        outputs = []
        for neuron in self.neurons:
            outputs.append(neuron.output)
        return outputs

class Neuron:
    def __init__(self, bias):
        self.bias = bias
        self.weights = []

    def calculate_output(self, inputs):
        self.inputs = inputs
        self.output = self.squash(self.calculate_total_net_input())
        return self.output

    #
    def calculate_total_net_input(self):
        total = 0
        for i in range(len(self.inputs)):
            total += self.inputs[i] * self.weights[i]
        return total + self.bias

    # 激活函数sigmoid
    def squash(self, total_net_input):
        return 1 / (1 + math.exp(-total_net_input))


    def calculate_pd_error_wrt_total_net_input(self, target_output):
        return self.calculate_pd_error_wrt_output(target_output) * self.calculate_pd_total_net_input_wrt_input();

    # 每一个神经元的误差是由平方差公式计算的
    def calculate_error(self, target_output):
        return 0.5 * (target_output - self.output) ** 2

    
    def calculate_pd_error_wrt_output(self, target_output):
        return -(target_output - self.output)

    
    def calculate_pd_total_net_input_wrt_input(self):
        return self.output * (1 - self.output)


    def calculate_pd_total_net_input_wrt_weight(self, index):
        return self.inputs[index]

'''
# 文中的例子:

nn = NeuralNetwork(2, 2, 2, hidden_layer_weights=[0.15, 0.2, 0.25, 0.3], hidden_layer_bias=0.35, output_layer_weights=[0.4, 0.45, 0.5, 0.55], output_layer_bias=0.6)
for i in range(10000):
    nn.train([0.05, 0.1], [0.01, 0.09])
    print(i, round(nn.calculate_total_error([[[0.05, 0.1], [0.01, 0.09]]]), 9))
'''

#另外一个例子，可以把上面的例子注释掉再运行一下:

training_sets = [
    [[0, 0], [0]],
    [[0, 1], [1]],
    [[1, 0], [1]],
    [[1, 1], [0]]
    ]

nn = NeuralNetwork(len(training_sets[0][0]), 5, len(training_sets[0][1]))
for i in range(10000):
      training_inputs, training_outputs = random.choice(training_sets)
      nn.train(training_inputs, training_outputs)
      print(i, nn.calculate_total_error(training_sets))

参考资料：https://blog.csdn.net/qq_42633819/article/details/82903871

                 https://www.cnblogs.com/charlotte77/p/5629865.html