2.一脚踹进ViT——Attention机制原理及实现

2.一脚踹进ViT——Attention机制原理及实现

同样是百度飞浆课程的笔记，视频中的图就拿来用了

1. 注意力（Attenetion）机制原理

先来看传统RNN结构如何最终演变到我们目前的注意力机制

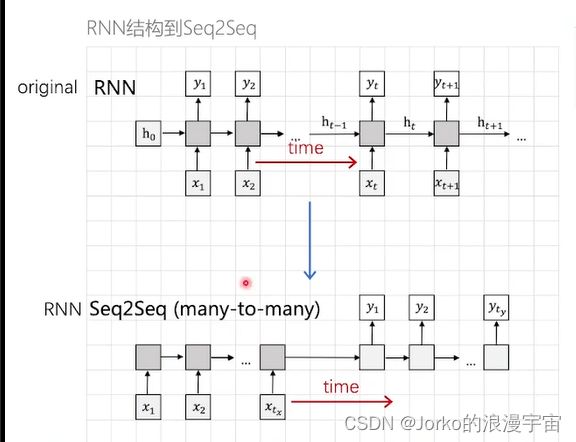
RNN灰色框代表一个模型，横轴是时间段，特点是，每一个时间点给一个输入，得到一个输入，同时会输出一个中间结果（隐变量）作为特征表达，并传给下一时间点，RNN存在的问题是：每一个输入对应一个输出，所以输入和输出需要是一样的，而当输入和输出长度不一样时，或者处理不是一对一问题时候，怎么办呢？

又提出了Seq2Seq，不用每个时间段的输入然后得到输出，只需要在tx时间段内，给定所有输入，灰色部分是同一个模型，依次输入模型后，然后再输出结果，所以能实现输入和输出长度不一的情况。

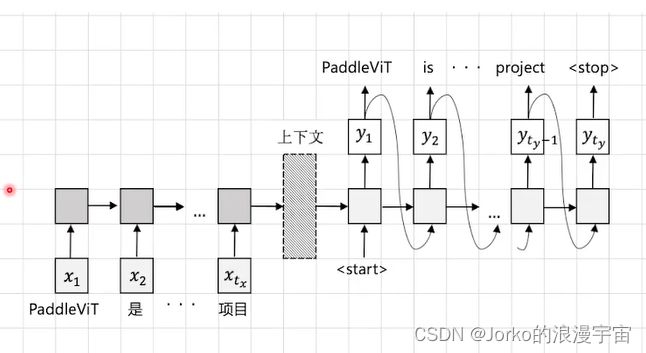
在Seq2Seq方式中，虽然能解决输入和输出不一致的问题，比如 输入可以是10个，输出可以是15个。但在每个时间段都输入了单词/tokens，所有这些信息都存在了模型当中一个叫Context/上下文/hidden state/隐变量中，每次更新在同一个位置，当句子很长时，因上下文保存信息能力有限，所以可能会影响输出，源语句的所有信息都是通过模型建模后存在上下文中的，如果上下文部分做的不好，结果做的就不好。

所以我们想能不能换一种方式，希望前面每一个时间段信息传递给解码部分呢？

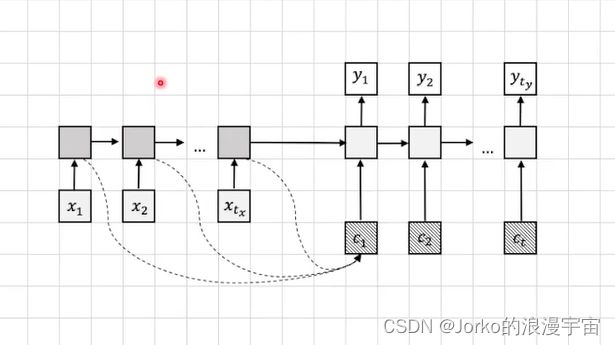
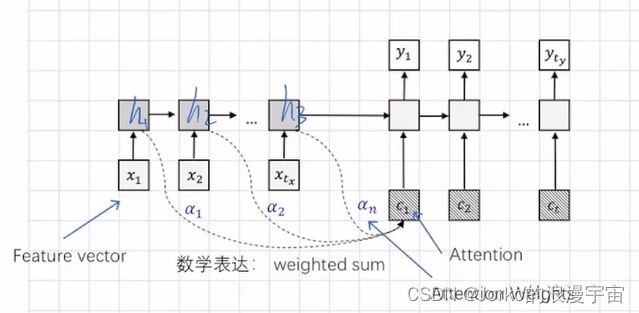
可以对隐变量多分出一个分支传递给解码器的输入当中，如图虚线部分，下图中我们除了h1，h2，h3，再保存一份α1，α2，α3传给Decoder，c就叫做attention，它看到前面所有时间点（整个句子中所有的单词信息），并将它们融合，给我们当前来用，而哪个更重要就是α1，α2，α3来控制，这个α就可以随机设置，但肯定不如让他学习好，我们可以将α变为可学习的参数， c1 = α1*h1+α2 *h2+……+αn *hn

刚才提到的是RNN和Seq2Seq的方式，其实在Transformer中也是需要注意力机制，将输入序列的信息融合进来传递给我们的解码器。

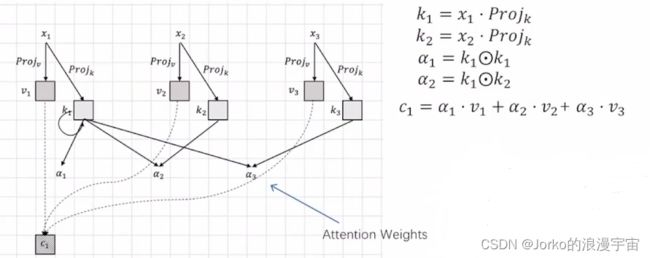
x1,x2,x3可以作为patch embedding，如果是图像就是1*96的feature vector，想让其进一步算attention，需要对x进行project（w）操作，将x变成更高维/更低维的特征表达，就是v，v再与α相乘，就得到了第一个位置的结果c1，同理得到c2，c3……

那如何让α变为可学习参数呢？

那就需要attention，对x1多做一次project，得到k1，让k1和自己去算得到α1，k1与k2得到α2，可以将α1、α2等当作一个单值/标量（scalar），并非一个向量，而x和k是feature vector，而得到k1、k2、k3都是通过同一个可学习的k，即projk得到，有了它们，我们的α也是可学习的

为什么要用两个向量的点乘？

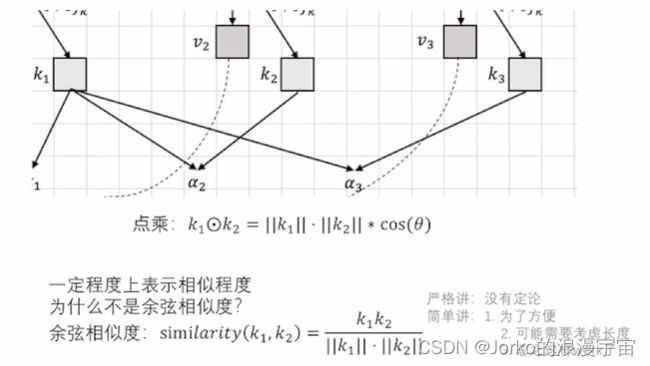
用两个向量各自的长度和空间中的夹角的cos值来计算点积，从而得到α，k1和k2一定程度表示相似度，也和余弦相似度很像，但没有除以他们的模。那k1和k2表示谁的相似度呢？上面是x1和x2，那x1和x2又是什么呢？ 比如一个句子 rabbit is eatting a carrot because it is hungry. 中，假设x1是rabbit，xn是it，我们希望模型让x1和xn相似，所以它的α就变大，越相似就接近，在编码的时候越关注这些信息，如果it指的是rabbit，那她算出来的αk就很大程度指向it，所以可以说是一定程度上表示相似程度，为什么是一定程度呢？因为和余弦相似度相比是没有除以各自的模的。

而为什么不用余弦相似度？可能是为了方便，也可能是需要考虑长度，如果取模之后长度就取标准化了。

这已经和transformer很相似了，那还差什么呢？

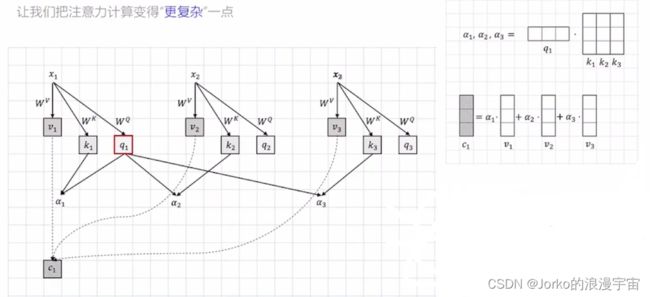
刚才k和自己算，每个k和其他的k算，我们现在更复杂，我们多了一个query，让key和q去算，q就是一个query，q与k计算后，就得到了一个attention的weight，即α，得到α向量后，与每个v相乘，就可以最终得到c1，其中q，k，v都是一个feature vector。针对x1的attention，以及c2是针对x2的attention，最终就可以得到我们的注意力了。

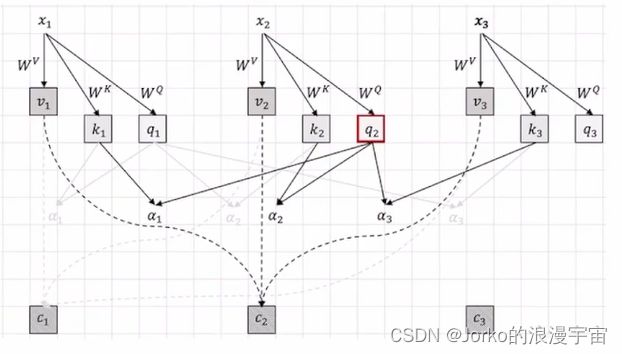
对x1去query看与其他句子的attention用它自己的q去算，算x2的attention时，用它自己的query与其他的k去算，这样做的好处：1.让模型更复杂，能有更强能力去建模；2.让索引和查询独立开，各做各的事情，所以，给谁做attention就用谁的query去算就可以了

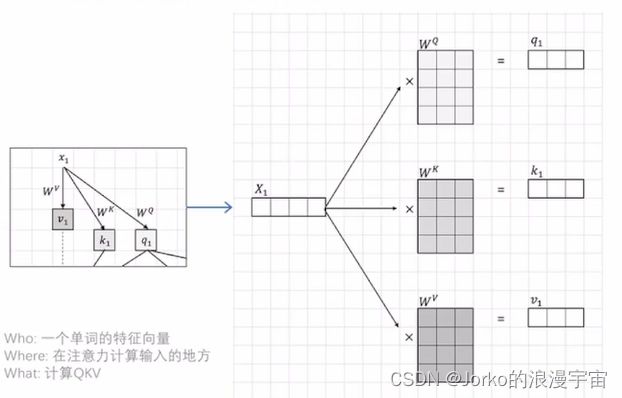
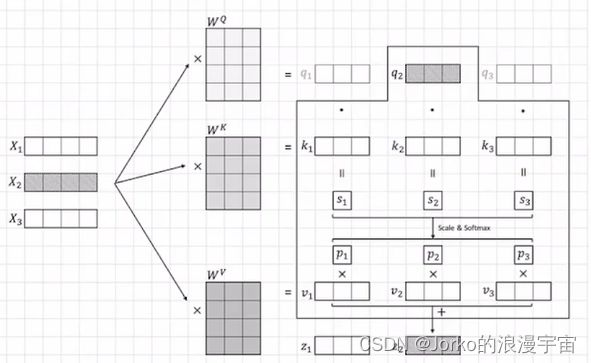
就举例 x1（刚才左上角的部分），假设embedding是1×4的feature vector，上一节中，我们得到了1×16的vector，就是这里传入的X，而WQ WK WV矩阵是可学习的参数，其形状我们可以自定，可以是4 ×任意数N，N就是embed_dim，你想得到的参数越多，可以设定越大，这里是3，我们对x进行一个proj/embed，其实就是一个矩阵运算，最终得到q1、k1、v1

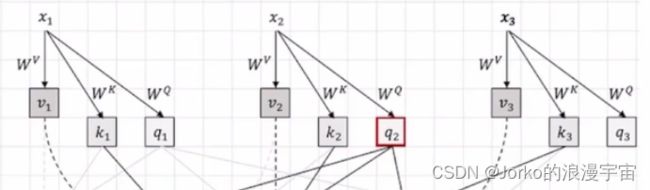
刚才仅对x1（patch/patch embedding/feature vector/一个序列中的一个token）做了操作，现在对x1，x2，x3做操作

注意Wq，Wk，Wv并不是一样的，他们是可学习的。

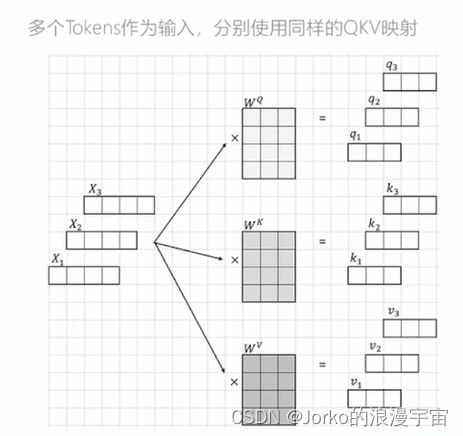
我们需要对所有的Xi（句子中的词/图片的patch）计算注意力

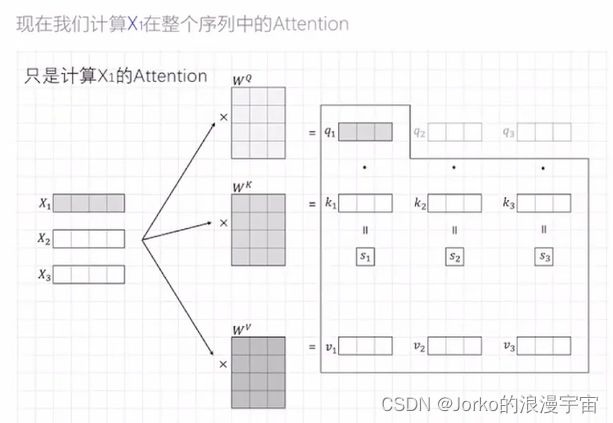
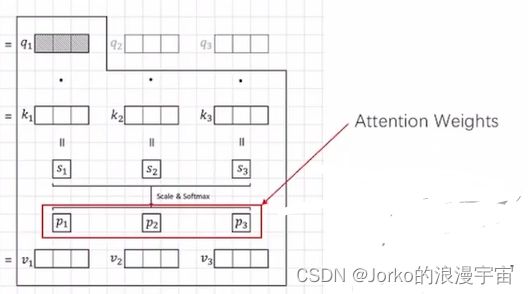
要对x1/x1单个的token计算attention，应该拿出当前token的query与所有其他单词的k去计算，包括他自己，q1与k1向量做点击可以得到s1，也可以写成下面矩阵形式，之后可以方便计算。

同样算出s2，s3

此时的s已经很接近我们叫做attention的东西了，此时需要做一个scale & softmax操作，scale就是给其乘以一个值，做一个数值的变换，softmax就是将s1……sn加和变为一个概率值，谁的概率大谁就更值得被注意，得到的p值就是attention weight，attention实际上来表达一个feature，表达的是token通过transformer/attention机制算出来的东西，它对于其他每个序列关注多少是一个概率，或者是一个比值，就是我们这里的p，有了p之后，要得到针对x1/q1的attention应该怎么做呢？

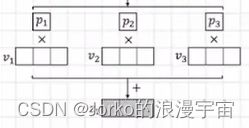
就拿p与v相乘，再加起来即可。此时的p1、p2、p3经过sacle操作后是scalar，就是一个值。

scale & softmax操作（实际叫scale for sofxmax，即我们scale的目的是为了做softmax），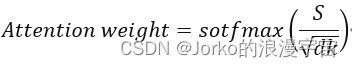
其中dk是指k的长度，也可以叫做embed_dim

那为什么要用dk？

• Variance（var）表示什么？

  在统计中Variance越大表示序列的波动越大，越小越平均

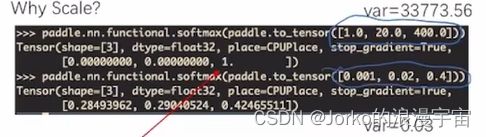
• 序列var越大，那么经过softmax越容易偏向大值

  

  他们的比例相同，但是方差相差很大，给他取softmax后，var大的序列偏向于更大的值

• 假设序列（feature）Q和K每一位独立的，并且是random variable（std=1，mean=0）

• 那么S（Q * KT）的方差就是d_k，我们希望注意力不能只注意最重要的，还需要把其他的句子稍微看一看，为了保证这个，所以我们需要将var拉到1.0，将各个部分都看一看

算完z1，算z2，z3到zn，针对x1有z1，针对x2有z2，针对每个x都有对应的z，所以输入多少个token，仍输出多少个feature，这部分就是Self Attention

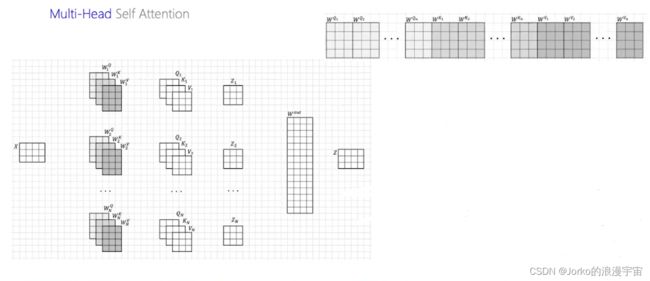
那Mult-Head Self Attention是什么呢？

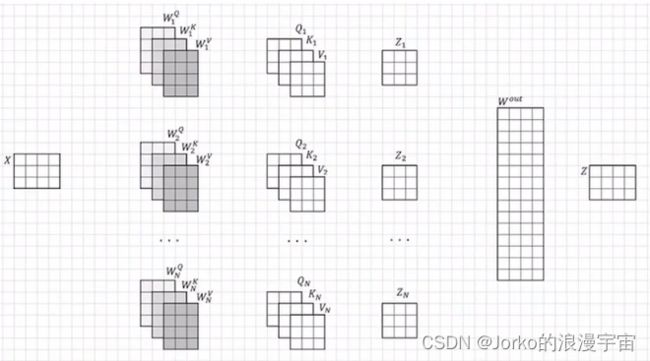
刚才用了WQ WK WV算出来的仅一个attention看的，对它们copy很多份，每个部分独立地看自己的信息，（需要注意：复制的QKV仅是从结构上复制，并非将weight复制，实际建网络中实际上是不同的weight，初始化虽然一样，但学习是不一样的，每一份都是学自己的）最终大家一起来决策，Mult-Head就是复制多次进行运算。

最终统一意见，用可学习参数Wout来得到最终的输出Z，它与X一样都是N行，X的列数根据embed_dim决定，而一般Z的列数也是embed_dim

单一向量运算转为矩阵运算

实际计算中，每一个feature vector 与权重矩阵运算，eg.如果对X1与QKV权重矩阵运算，再使用X2，这样效率不高，所以将多个Xi拼接成一个矩阵X，进行矩阵运算得到q矩阵，k矩阵，p矩阵，v矩阵以及最终的矩阵

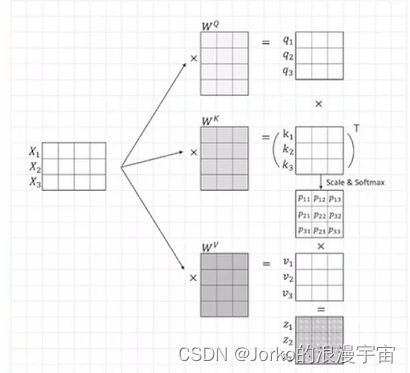
矩阵计算中，刚才输入是3×4，每个weight都是4×n，X矩阵与Wq进行矩阵运算得到q1q2q3，原本是q1点乘k1，现在变成Q与 K的转置相乘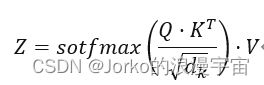

我们可以将X写为矩阵形式，Q K V 也能写成矩阵形式，那Q K V长的差不多能不能将它们拼接到一起呢？

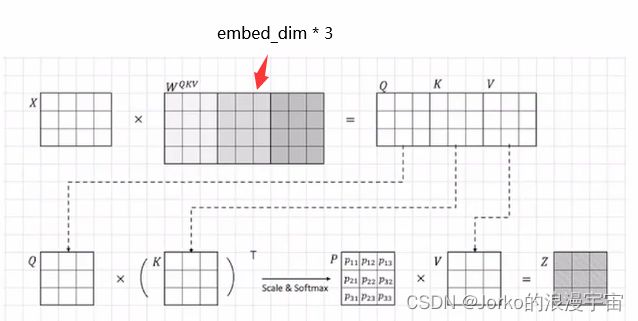
当然可以，将QKV放到一起，列数变为了embed_dim×3

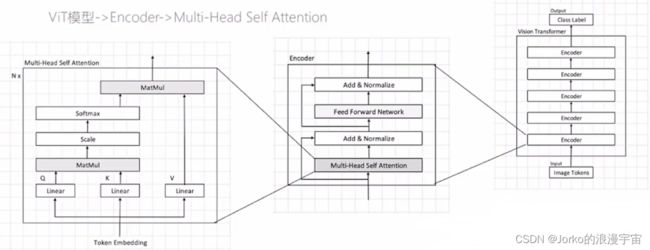
于是得到了ViT的整体架构，Image Token进入网络通过proj，变成Q K V，每个Q与其他K算出注意力（用矩阵乘法），再通过Scale、Softmax将其稳定下来，最后再与V相乘，得到输出，即Attention。

之后进入上节的网络Encoder编码器中

2.实践部分

理论部分已经完毕了，接下来就是实践部分，我们其实就是实现MSA

同样先构建我们的三步：主函数，入口创建，Attention类创建

import torch
import torch.nn as nn
torch.device('cpu')

class Attention(nn.Module):
    def __init__(self,embed_dim, num_heads, qkv_bias=False, qk_scale=None,dropout=0.,attention_dropout=0.):
        super().__init__()

    def forward(self,x):
      
        return out

def main():
    # batch_size=8,4*4的patch，最终变为96维的features，此时的t就是patch embed图像的image tokens,
    t = torch.randn([8,16,96])
    model = Attention(embed_dim=96, num_heads=4, qkv_bias=False, qk_scale=None)
    print(model)
    out = model(t)
    print(out.shape)

if __name__ == '__main__':
    main()

因为要实现多头，所以不仅要定义embed_dim、num_heads，还要定义每个头的head_dim，多头他最后将各部分的进行拼接

在transpose_multi_head 函数中，刚开始Q、K、V权重矩阵都是[B, N ,all_head_dim]，本文all_head_dim就是embed_dim=96，为了防止多头划分时，出现非整数，所以将head_dim与num_heads相乘得到整数all_head_dim。而reshape后，将前两维保留加上了num_heads和head_dim，我们此处的N其实就是num_patch=16。

前向函数得到q，k，v后，将头的数量放在前面，每个头单独去做，每个patch中的图像也单独去做，真正就是每个num_patches的head_dim去相乘，经过q和k运算后，scale和softmax不改变维度，最后atten[B, num_heads, num_patches, num_patches]，其实是每个patches与所有patches的attention，所以一定是N×N的，它的每一个值就是当前行的值，对应一列的值。

知道attn是 N×N的，而V是num_dim×head_dim，他俩一相乘，又乘回来了，再做一次0213，就把维度转回来[B, num_heads, num_patches, head_dim] ，才能做Linear， 此时proj层的输入应该是all_head_dim，所以需要Reshape后两个维度reshape([B, N, -1])

本实现实际没有用到dropout，一般它加载attention层之后或者Linear层后，但在ViT中，Dropout的参数设置的是0，实际中没用

完整代码如下：

import torch

import torch.nn as nn

torch.device('cpu')

class Attention(nn.Module):
    def __init__(self,embed_dim, num_heads, qkv_bias=False, qk_scale=None,dropout=0.,attention_dropout=0.):
        super().__init__()
        self.embed_dim =embed_dim
        self.num_heads =num_heads
        self.head_dim = int(embed_dim/num_heads)
        self.all_head_dim = self.head_dim*num_heads
        # 把所有q 写在一起， 所有k、V写在一起，然后拼接起来，前1/3代表了所有head的Q，每一个head的尺寸已经定义好，要用的时候切就行了
        self.qkv = nn.Linear(embed_dim,
                             self.all_head_dim*3,
                             bias=False if qkv_bias is False else None)
        self.scale = self.head_dim ** -0.5 if qk_scale is None else qk_scale
        self.softmax = nn.Softmax(-1)
        self.proj = nn.Linear(self.all_head_dim,embed_dim)

    def transpose_multi_head(self,x):
        # x: [B, N, all_head_dim]
        new_shape = x.shape[:-1] + (self.num_heads, self.head_dim)
        x = x.reshape(new_shape)
        # x: [B, N, num_heads, head_dim]
        x = x.permute(0,2,1,3)
        # x: [B, num_heads, num_patches, head_dim]
        return x


    def forward(self,x):

        B,N ,_ = x.shape
        qkv = self.qkv(x).chunk(3,-1)
        # [B, N, all_head_dim]* 3 ， map将输入的list中的三部分分别传入function，然后将输出存到q k v中
        q, k, v = map(self.transpose_multi_head,qkv)
        # q,k,v: [B, num_heads, num_patches, head_dim]
        attn = torch.matmul(q,k.transpose(-1,-2))   #q * k'
        attn = self.scale * attn
        attn = self.softmax(attn)
        attn_weight = attn
        # dropout
        # attn: [B, num_heads, num_patches, num_patches]

        out = torch.matmul(attn, v)  # 不需要转置，这里softmax(scale*(q*k')) * v
        out = out.permute(0,2,1,3)
        # out: [B,  num_patches,num_heads, head_dim]
        out = out.reshape([B, N, -1])

        out = self.proj(out)
        #dropout

        return out,attn_weight

def main():
    t = torch.randn([8,16,96])
    model = Attention(embed_dim=96, num_heads=4, qkv_bias=False, qk_scale=None)
    print(model)
    out,w = model(t)
    print(out.shape)
    # w的维度，16*16是16个patch，每个要看它与别人的自注意力，而4是多头注意力机制，每个人看自己
    print(w.shape)


if __name__ == '__main__':
    main()

可以看到经过attention层后输出和输入一样，我们并没有改变它的维度，8仍然是Batch_size，16是num_patches，每个patch算它的注意力，虽然做了多个头并没改变96这个地方；而attention中的权重部分就是4个头其中每个patch对其他patch的注意力，最终将各个头的维度进行融合，用头的个数4乘以每个头的维度24又恢复到了96维上

torch.Size([8, 16, 96])

torch.Size([8, 4, 16, 16])
由此ViT中Attention部分已经实现完成，需要反复巩固内容，内容有点绕，好啦！拜拜~