pytorch 张量tensor的自动微分(求导)
意义:PyTorch张量可以记住它们自己从何而来,根据产生它们的操作和父张量,它们可以根据输入自动提供这些操作的导数链。这意味着我们不需要手动推导模型,给定一个前向表达式,无论嵌套方式如何,PyTorch都会自动提供表达式相对其输入参数的梯度。
- 将Torch.Tensor属性 .requires_grad 设置为True,
- pytorch将开始跟踪对此张量的所有操作。
- 完成计算后,可以调用 .backward() 并自动计算所有梯度。
- 该张量的梯度将累加到.grad属性中。
注意:默认不会自动求导,记住链式求导的过程很耗内层,它在偷懒!
# 进行张量运算
y = x + 2
# y是由于运算而创建的,因此具有grad_fn属性
print(y.grad_fn)
# 输出:
y 作为操作的结果被创建,所以它有 grad_fn
默认每一个节点都有这个属性 grad_fn,它指示梯度函数是哪种类型,叶子节点通常为None,只有结果节点的grad_fn才有效
注意:根节点都是一个标量(即一个数)。
导数必须由标量输出创建,即最后输出的结果,必须是一个标量,不能是向量,这里y是一个矩阵,所以报错
导数定义:当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时,函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数。即一个函数在某一点的导数描述了这个函数在这一点附近的变化率。
神经网络中我们的目标函数即损失函数,都是标量函数!!!!
如果结果节点是一个标量,当调用它的backward方法后会根据 ”链式求导法则“ 自动计算出各叶子节点的梯度值。
如何解决矩阵无法直接求导:
那么我们只要想办法把矩阵转变成一个标量不就好了。
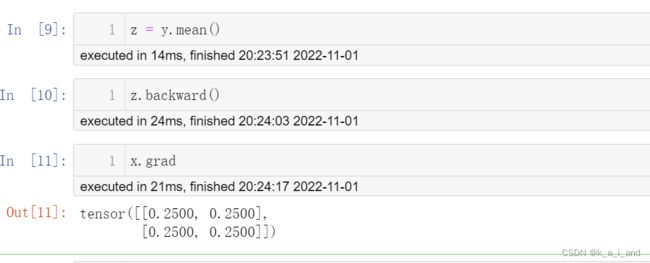
这里我 将y求平均值后变标量(或其他操作也可以,只要能把它变成标量),此时才可以反向求导
注意:只有执行完backward之后,所有requests_grad=True的变量的导数才能自动求出(叶子节点,可多个),即我的代码顺序如下图显示0.2
0.25如何来的呢?y求导后求平均值,再和x相乘 ==d(z)/d(y)*d(y)/d(x)?啊哈,好像还是不理解
知识点:关于Tensor为向量(矩阵)时,计算对叶子节点向量(矩阵)的导数
计算图模型:pytorch是动态图机制,所以在训练模型时候,每迭代一次都会构建一个新的计算图。而计算图其实就是代表程序中变量之间的关系。
在网络backward时候,需要用链式求导法则求出网络最后输出的梯度,然后再对网络进行优化
当根节点(即:函数的因变量)为一个向量的时候,会构建多个计算图对该向量中的每一个元素分别进行求导。
参考这篇文章
- 如果是标量对向量求导(scalar对tensor求导),那么就可以保证上面的计算图的根节点只有一个,此时不用引入grad_tensors参数,直接调用backward函数即可
- 如果是(向量)矩阵对(向量)矩阵求导(tensor对tensor求导),实际上是先求出Jacobian矩阵中每一个元素的梯度值(每一个元素的梯度值的求解过程对应上面的计算图的求解方法),然后将这个Jacobian矩阵与grad_tensors参数对应的矩阵进行对应的点乘,得到最终的结果。
————————————————
版权声明:本文为CSDN博主「Yale曼陀罗」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/weixin_42782150/article/details/106116082
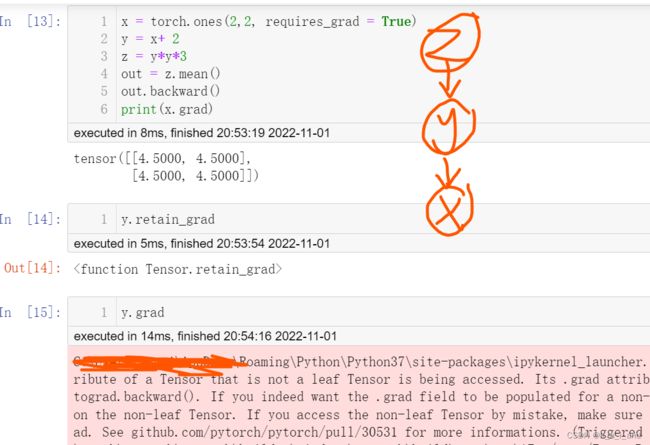
求非叶子节点的tensor的导数,必须使用retain_grad,否则报错,用.retain_grad注意后面没有括号哈!
啥是叶子节点:节点就是参与运算的变量,而由用户自己创建的Variable变量,也就是用torch.rand()等语句创建的
代码解读:out = f(x)
自动微分运算, 注意 out 是标量值
打印梯度 d(out)/ dx
不需要跟踪计算微分
with torch.no_grad()
当张量的 requires_grad 属性为 True 时,
pytorch会一直跟踪记录此张量的运算,也就是这个参数告诉PyTorch跟踪由对x张量进行操作后产生的张量的整个系谱树。
任何将x作为祖先的张量都可以访问从x到那个张量调用的函数链。如果这些函数是可微的(大多数PyTorch张量操作都是可微的),导数的值将自动填充为params张量的grad属性。
当不需要跟踪计算时,可以通过将代码块包装在 with torch.no_grad(): 上下文中
print(x.requires_grad)
print((x ** 2).requires_grad)
#只要x可以自动微分,带有它的变量都可以沾光
with torch.no_grad():
print((x ** 2).requires_grad)
'''
True
True
False
''' 也可使用 .detach() 来获得具有相同内容但不需要跟踪运算的新Tensor :detach 脱离
print(x.requires_grad)
y = x.detach()
print(y.requires_grad)
# True
# False
除了在定义张量时使用requires_grad,还可以使用 requires_grad_ 就地改变张量此属性:(还记得前面我们说的加下划线会修改原来的tensor吗)
a = torch.randn(2, 2)
a = a*3 + 2
print(a.requires_grad)
# 输出 False
a.requires_grad_(True)
print(a.requires_grad)
# 输出True