机器学习--决策树的创建与实现

决策树

    定义

    实现

    可视化

    总结

一、决策树的定义 

1.决策树的概念

    决策树(decision tree)是一种基本的分类与回归方法。决策树模型呈树形结构，在分类问题中，表示基于特征对实例进行分类的过程。它可以认为是if-then规则的集合，也可以认为是定义在特征空间与类空间上的条件概率分布。

     决策树是一种描述对实例进行分类的树形结构，其中每个内部节点表示一个属性上的判断，每个分支代表一个判断结果的输出，最后每个叶节点代表一种分类结果，本质是一颗由多个判断节点组成的树。分类决策树模型是一种树形结构。 决策树由结点和有向边组成。结点有两种类型：内部结点和叶节点。内部结点表示一个特征或属性，叶节点表示一个类。

2.决策树的分类举例

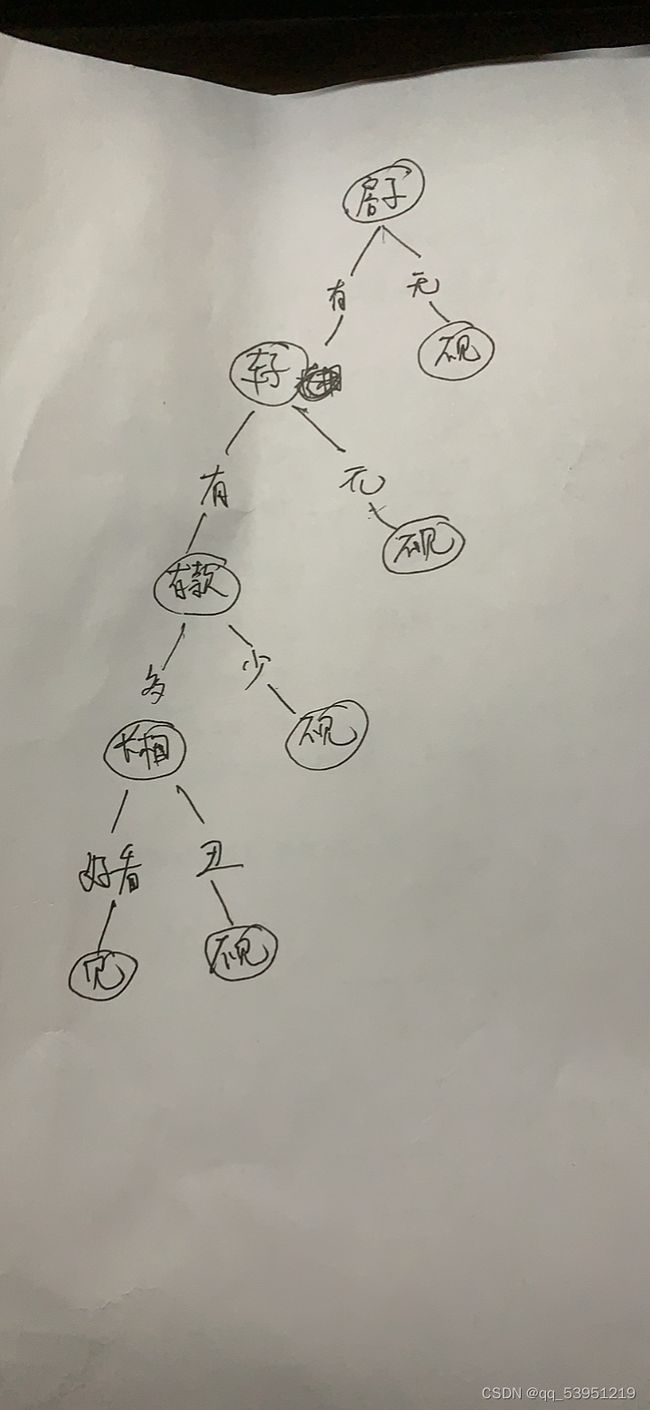
    简单来说，决策树的思想在我们生活中很常见，比如现在很棘手的问题，你想相亲找对象，对面一上来就问你，有房没房，有车没车，然后有没有存款，就算都有搞不好还得看你好不好看

    根据上面条件，如下画出找对象的决策树，可以看到其中每个内部节点表示一个属性上的判断，每个分支代表一个判断结果的输出，最后每个叶节点代表一种分类结果。

    总而言之，分类决策树模型是一种描述对实例进行分类的树形结构。通过很多次判断来决定是否符合某类的特征。

    决策过程中提出的每个判定问题都是对某个属性的“测试” ，每个测试的结果或是导出最终结论，或者导出进一步的判定问 题，其考虑范围是在上次决策结果的限定范围之内， 从根结点到每个叶结点的路径对应了一个判定测试序列。

     决策树学习的目的是为了产生一棵泛化能力强， 即处理未见示例能力强的决策树。

3.决策树的一般步骤

决策树通常有三个步骤：特征选择、决策树的生成、决策树的修剪。

特征选择：从训练数据的特征中选择一个特征作为当前节点的分裂标准（特征选择的标准不同产生了不同的特征决策树算法）。
决策树生成：根据所选特征评估标准，从上至下递归地生成子节点，直到数据集不可分则停止决策树停止声场。
决策树剪枝：决策树容易过拟合，需要剪枝来缩小树的结构和规模（包括预剪枝和后剪枝）。
 

4.决策树的优缺点

    之前博客的k-近邻算法的分类任务，但是其最大的缺点是无法给出数据的内在含义，决策树的优势在于数据形式非常容易理解。

优点：

计算复杂度不高，输出结果易理解，对中间值缺失不敏感，可以处理不相关特征数据。
准确性高: 挖掘出来的分类规则准确性高, 便于理解, 决策树可以清晰的显示哪些字段比较重要, 即可以生成可以理解的规则。
可以处理连续和离散字段、不需要任何领域知识和参数假设、适合高维数据。
缺点：

对于各类别样本数量不一致的数据, 信息增益偏向于那些更多数值的特征。
容易过拟合、忽略属性之间的相关性。
适用数据类型：数值型和标称型
 

二、决策树的实现

1.一般流程

(1) 收集数据：可以使用任何方法。
(2) 准备数据：树构造算法只是用于标称型数据，因此数值型数据必须离散化。
(3) 分析数据：可以使用任何方法，决策树构造完成后，可以检查决策树图形是否符合预期。
(4) 训练算法：构造一个决策树的数据结构。
(5) 测试算法：使用经验树计算错误率。当错误率达到可接收范围，此决策树就可投放使用。
(6) 使用算法：此步骤可以使用适用于任何监督学习算法，而使用决策树可以更好地理解数据的内在含义。
 

2.实战

我选择的环境是vscode，虚拟环境用anaconda，使用ipynb。

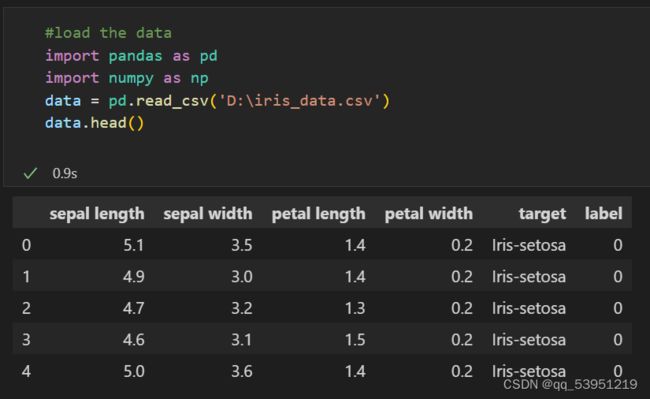
我的数据集有3类花，每种花有4个特征。把4个特征投影到二维平面可以很清楚看出。setosa与其余两种鸢尾花有明显的边界，而versicolor和virginica这两种花具有相似的特征，看起来有些重叠。
如果是人为判断的话，我们可以这样想，setosa与其余两种花区别最大的特征就作为第一个分叉。
如果满足那么全是setosa，不满足则是其余2种，则再进行判断。
 

 

 

150个样本，每个样本有4个维度的特征。
接下来就是构建决策树模型了。

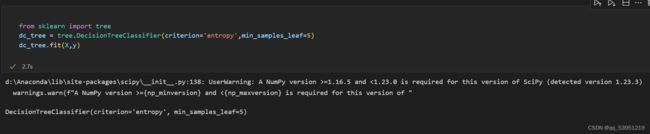
在可以评测哪个数据划分方式是最好的数据划分之前，集合信息的度量方式称为信息熵或者简称为熵(entropy)，常见的计算信息熵有3种，ID3，C4.5，CART。 

criterion='entropy’也就是采用ID3。
min_samples_leaf：叶子节点最少样本数，可选参数，默认是1。这个值限制了叶子节点最少的样本数，如果某叶子节点数目小于样本数，则会和兄弟节点一起被剪枝。叶结点需要最少的样本数，也就是最后到叶结点，需要多少个样本才能算一个叶结点。如果设置为1，哪怕这个类别只有1个样本，决策树也会构建出来。如果min_samples_leaf是整数，那么min_samples_leaf作为最小的样本数。如果是浮点数，那么min_samples_leaf就是一个百分比，同上，celi(min_samples_leaf * n_samples)，数是向上取整的。如果样本量不大，不需要管这个值。如果样本量数量级非常大，则推荐增大这个值。
这里我们先选择5试试。

 导入评判正确率的函数，预测和真实值进行比较得出正确率97%，还是很不错的。

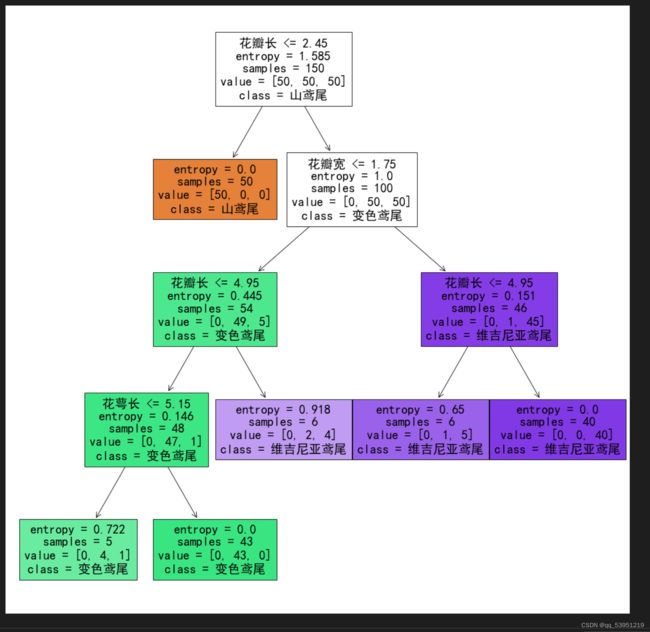
三.决策树可视化

feature_names=[‘花萼长’, ‘花萼宽’, ‘花瓣长’, ‘花瓣宽’],这就是一些特征。
class_names=[‘山鸢尾’, ‘变色鸢尾’, ‘维吉尼亚鸢尾’]，这些是标签。

不知道为啥跑出了错误，但还是照样有决策树，我后面再进行纠正一下

 

     min_samples_leaf有点的控制树的深度的意思，但是不是简单的值为多少深度就是多少。它是通过样本数来控制深度。如果再分下去的某个分支样本数小于5那么它就不会再分了。
如果想要直接控制深度的话，这里还有个参数是max_depth，这个参数值是多少那么决策树的深度就是多少了。
 

     为了展示min_samples_leaf如何控制决策树，我再令值为10再进行可视化看看。

可以看到最后的sample样本数都是大于等于10的，它不会继续往下分，深度才5。而上面min_samples_leaf=5时候最后的sample是大于等于5的，深度为6。

四、评价

对于本次实战

优点：

易于理解和解释。决策树可以可视化。
几乎不需要数据预处理。其他方法经常需要数据标准化，创建虚拟变量和删除缺失值。
可以处理多值输出变量问题。
预测正确率达到了97%，准确率高。

缺点：

参数比较多，不同的参数对于决策树的结构影响较大，从而结果也会有些偏差。
决策树学习可能创建一个过于复杂的树，并不能很好的预测数据。也就是过拟合。      

实验总结：

    决策树，其实和KNN算法的目的是一样的，就是做分类任务。对于我这次实验，最基本的就是懂得了ID3、C4.5、CART三种算法。一开始对信息熵、信息增益、信息增益率、基尼指数，不太理解，突然来的新东西需要时间消化，比较困难的地方是用Matplotlib绘制决策树，那个代码比较难理解，而且对于python3的环境，有些函数已经更新了，也导致了过程中的报错。

    还有一个就是，python用字典结构存储决策树，是我没有想到的，花了一点点时间才看明白，然后对于实战中的报错，其实也就普通的路径里的文件与目录的问题，无伤大雅。