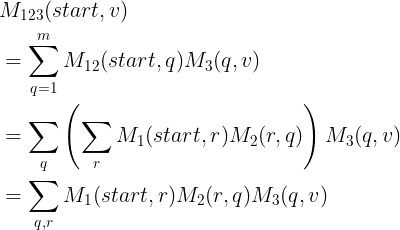条件随机场CRF(Conditional Random Field)
⼀个重要的要求是,我们保留了推断的⾼效算法,它与链的长度是线性关系。例如,这要求,在给定观测![]() 的条件下,表⽰
的条件下,表⽰![]() 的后验概率分布的量
的后验概率分布的量![]() 在与转移概率
在与转移概率![]() 和发射概率
和发射概率![]() 相乘然后在
相乘然后在![]() 上求和或积分之后,我们得到的
上求和或积分之后,我们得到的![]() 上的概率分布与
上的概率分布与![]() 上的概率分布具有相同的函数形式。这就是说,在每个阶段概率分布不可以变得更复杂,而仅仅是在参数值上发生改变。毫不令人惊讶的是,在多次相乘之后具有这个性质的唯一的分布就是指数族分布。实际应用中最重要的一个例子就是高斯分布。 ——PRML
上的概率分布具有相同的函数形式。这就是说,在每个阶段概率分布不可以变得更复杂,而仅仅是在参数值上发生改变。毫不令人惊讶的是,在多次相乘之后具有这个性质的唯一的分布就是指数族分布。实际应用中最重要的一个例子就是高斯分布。 ——PRML
目录
--------七月在线机器学习笔记
logistic 回归
logistic sigmoid的反函数
对数线性模型的一般形式:
特征函数的选择
词性标注的特征函数:
词性标注的三个问题
线性条件随机场
次特征
CRF的三个问题
概率计算问题
参数学习问题
预测问题
CRF部分理论解释
无向图模型
条件随机场
DGM转换成UGM
MRF的性质
团和最大团
Hammersley-Clifford定理
CRF总结
--------七月在线机器学习笔记
logistic 回归
考虑二分类的情形。
类别C1的后验概率可以写成
(2)
且
是sigmoid函数。“sigmoid”的意思是“S形”。这种函数有时被称为“挤压函数”,因为它把整个实数轴映射到了⼀个有限的区间中。在许多分类算法中都有着重要的作⽤。
满足下面的对称性:
(3)
且
对于广义线性模型:类别C1的后验概率可以写成作⽤在特征向量ϕ的线性函数上的logistic sigmoid函数的形式,即
极大似然估计:
似然函数
取对数得
求偏导
(8)
那么,Logistic回归参数的学习规则:
目标函数
是一个凹函数(二阶导小于0),因此这里是顺梯度方向
它与 当所有点都有各自独立的分布时,整体服从高斯分布(中心极限定理)的线性回归的参数学习(最小二乘)具有相同的形式
对于K>2个类别的情形
(11)
即softmax函数(归一化指数)
logistic sigmoid的反函数
一个事件的几率odds,是指该事件发生的概率与不发生的概率的比值。
被称为logit (odds)函数 。 因其取对数后是线性的,因此称作对数线性模型
对数线性模型的一般形式:
令x为某样本,y是x的可能标记,将logistic/softmax回归的特征
记做
。
因此本质上
与
是成正比的,而
只是归一化因子。
因此,对数线性模型的一般形式为:
其中归一化因子【对公式(13)两边对y加和,则左边为1,故得到】:
那么给定x,预测标记为【分析公式(14)】:
即 ,在给定x和学习参数w,得到标记
的概率,遍历所有的y,取概率最大的y作为标记。
特征函数的选择
特征函数几乎可以任意选择,甚至特征函数间重叠。比如
词性标注的特征函数:
词性标注是指将,每个单词标记为名词/动词/形容词/介词等。
词性:POS,Part Of Speech
记w为句子s的某个单词,则特征函数可以是:
1.w在句首/句尾(位置相关)
2.w的前缀是anti-/co-/inter-等(单词本身)
3.w的后缀是-able/-ation/-er/-ing等(单词本身)
4.w前面的单词是a/could/SALUTATION等(单词间)
5.w后面的单词是am/is/are/等(单词间)
6.w前面两个单词是would like/there be等(单词和句子)
高精度的POS会使用超过10万个特征
注意:每个特征只和当前词性有关,最多只和相邻词的词性有关;
但特征可以和所有词有关
比如,下图所示:Y2只与前一个状态Y1有关,但Y2或Y1可以与整个X序列有关
词性标注的三个问题
词性标注被称为“结构化预测”,该任务与标准的类别学习任务存在巨大不同:
1)如果每个单词分别预测,将丢失众多信息;
--相邻单词的标记是相互影响的,非独立。
2)不同的句子有不同的长度;
--这导致不方便将所有句子统一成相同长度向量【尽管有类似的one-hot编码,但用于做词性标注代价过高】
3)标记序列解集与句子长度呈指数级增长
--如上图所示,解集有
个;这使得穷举法几乎无法使用
线性条件随机场
设X=(X1,X2…Xn)和Y=(Y1,Y2…Yn)均为线性链表示的随机变量序列,若在给定随机变量序列X的条件下,随机变量序列Y的条件概率分布P(Y|X)构成条件随机场,即满足马尔科夫性
则称P(Y|X)为线性链条件随机场。
在标注问题中,![]() 表示输入序列或称观测序列(n个词的序列),
表示输入序列或称观测序列(n个词的序列),![]() 表述对应的输出标记序列或称状态序列(词性)。
表述对应的输出标记序列或称状态序列(词性)。
定义,同公式(14):
次特征
定义句子![]() 的第
的第![]() 个特征
个特征![]() 是由若干次特征
是由若干次特征![]() 组合而成的,这里的
组合而成的,这里的![]() 依赖或部分依赖【当前词的状态可能与前一个词的状态无关】于当前整个句子
依赖或部分依赖【当前词的状态可能与前一个词的状态无关】于当前整个句子![]() 、当前词的标记
、当前词的标记![]() 、前一个词的标记
、前一个词的标记![]() 、当前词在句子中的位置
、当前词在句子中的位置![]() 。
。
将每个位置![]() 上的次特征
上的次特征![]() 相加,即得到特征
相加,即得到特征![]() ,从而解决训练样本变长的问题。
,从而解决训练样本变长的问题。
CRF的三个问题
1)CRF的概率计算问题
前向后向算法
2)CRF的参数学习问题IIS:改进的迭代尺度算法
3)CRF的预测算法Viterbi算法
概率计算问题
给定一组训练样本(x,y)找出权向量w,使得公式(16)成立:
![]()
满足上式的w,即为最终的推断参数
参数推断的两个难点
1) 如果给定x和w,如何计算哪个标记序列y的概率最大?--前面词性标注问题3)-指数级
2) 如果给定x和w,p(y|x,w)本身如何计算?
----归一化因子
与所有的可行标记
有关,不容易计算
状态关系矩阵
根据公式(18),
的分子部分可以化简为:
(20)
对应
的状态转移矩阵【m为标记(词性)的数目】
经过上述转换,问题变为对状态转移矩阵
先求
,然后进行矩阵连乘。
同理,分母部分
(22)
那么,定义
的矩阵
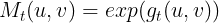
因为起始位置的词没有依赖
;结束位置词没有依赖
;
对于
,任选 某u=start状态
对于
,任选某v=stop状态
矩阵连乘:
从而,
时间复杂度:
那么,就得到了CRF的矩阵形式
前向-后向算法
与前面HMM类似,定义
为前向得分(概率),表示第k个词的标记为v的得分值(将得分值归一化后即为概率,这里只取分子部分)
得到递推公式:
(26)
注意:
为m维列向量,因此矩阵相乘时应转置为行向量
同样,定义后向得分
,表示第k个词的标记为v,且从k+1往后的部分序列标记的得分:
递推公式:
(27)
前向-后向关系:
与HMM类似,分析得出,
,这里1 是元素均为1的m维列向量。 (29)
概率计算:
单个状态的概率:
联合状态概率:
参数学习问题

对于监督学习,根据训练集合(x,y)直接用大数定理:频率估计概率P(x,y)
方法:求对数目标函数的驻点
公式(17):
取对数
求偏导(计算梯度)
(32)
梯度上升:
(33)
预测问题
根据上面公式(19)和公式(18),得
(34)
经过上述转换,问题变成求![]() 的加和最大问题,然而
的加和最大问题,然而![]() 就对应
就对应![]() 的状态转移矩阵【m为标记(词性)的数目】
的状态转移矩阵【m为标记(词性)的数目】
使用Viterbi算法,
类似于前向得分
利用前向概率选择最大标记序列
称
为前向得分(概率),表示第k个词的标记为v的最大得分值(将得分值归一化后即为概率),
得递推公式:
(23)
时间复杂度:
,标记数目为m,句子包含的单词数目为n
CRF是判别模型——给定x,判断P(y|x,w)的概率;HMM/LDA是生成模型——
![]()
CRF部分理论解释
无向图模型
NB-Naive Bayesian
有向图模型,又称作贝叶斯网络(Directed Graphical Models, DGM, Bayesian Network)
--事实上,在有些情况下,强制对某些结点之间的边增加 方向是不合适的。
使用没有方向的无向边,形成了无向图模型 (Undirected Graphical Model,UGM), 又称马尔科夫随机场或马尔科夫网络(Markov Random Field, MRF or Markov network)
条件随机场
设X=(X1,X2…Xn)和Y=(Y1,Y2…Ym)都是联合随机变量,若随机变量Y构成一个无向图G=(V,E)表示的马尔科夫随机场(MRF),则条件概率分布P(Y|X)称为条件随机场(Conditional Random Field, CRF)
X称为输入变量、观测序列
Y称为输出序列、标记序列、状态序列
大量文献将MRF和CRF混用,包括经典著作。
一般而言,MRF是关于隐变量(状态变量、标记变量)的图模型,而给定观测变量后考察隐变量的条件概率,即为CRF。
但这种混用,类似较真总理和周恩来的区别。有时候没必要区分的那么严格
混用的原因:在计算P(Y|X)时需要将X也纳入MRF中一起考虑
DGM转换成UGM
约定俗成的方法是,将有向边转换成无向边,将有共同孩子的结点之间连接
----注意:这样可能导致信息量发生了变化,比如上图,对于贝叶斯网络,给定2时,4和5应该是条件独立的;但是转换成马尔科夫网络,4和5之间有边连接,则结点间的信息相互独立性已经发生变化,也就是条件独立性的破坏【这样做的原因可能是变化影响相对较小】
MRF的性质
成对马尔科夫性(parewise Markov property)
设u和v是无向图G中任意两个没有边直接连接的结点,G中其他结点的集合记做O;则 在给定随机变量Yo的条件下,随机变量Yu 和Yv条件独立。
即:
局部马尔科夫性(local Markov property)
设v是无向图G中任意一个结点,W是与v有 边相连的所有结点,G中其他结点记做O; 则在给定随机变量Yw的条件下,随机变量 Yv和Yo条件独立。
即:
全局马尔科夫性(global Markov property)
设结点集合A,B是在无向图G中被结点集合 C分开的任意结点集合,则在给定随机变量 YC的条件下,随机变量YA和YB条件独立。
即:
举例,
三个性质的等价性
根据全局马尔科夫性,能够得到局部马尔科夫性;
根据局部马尔科夫性,能够得到成对马尔科夫性;
根据成对马尔科夫性,能够得到全局马尔科夫性;
事实上,这个性质对MRF具有决定性作用:
满足这三个性质(或其一)的无向图,称为MRF。
团和最大团
无向图G中的某个子图S,若S中任何两个结 点均有边,则S称作G的团(Clique)。
若C是G的一个团,并且不能再加入任何一个G 的结点使其称为团,则C称作G的最大团 (Maximal Clique)。
举例
团:{1,2}, {1,3}, {2,3}, {2,4}, {3,4}, {3,5},{1,2,3}, {2,3,4}
最大团:{1,2,3}, {2,3,4}, {3,5}
Hammersley-Clifford定理
UGM的联合分布可以表示成最大团上的随机变量的函数的乘积的形式;这个操作叫做UGM的因子分解 (Factorization)。
比如上图的联合分布可以表示为:
UGM的联合概率分布P(Y)可以表示成如下形式:
其中,C是G的最大团,![]() 是C上定义的严格正函数,被称作势函数(Potential Function)。因子分解是在UGM所有的最大团 上进行的。
是C上定义的严格正函数,被称作势函数(Potential Function)。因子分解是在UGM所有的最大团 上进行的。
CRF总结
条件随机场是给定输入的条件下,关于输出的条件概率分布模型,根据Hammersley-Clifford定理,可以分解成若干关于最大团的非负函数的乘积,因此,常常将其表示为参数化的对数线性模型。
线性链条件随机场使用对数线性模型,关注无向图边的转移特征和点的状态特征,并对每个特征函数给出各自的权值。
概率计算常常使用前向-后向算法;
参数学习使用MLE建立目标函数,采用IIS做参数优化;
线性链条件随机场的应用是标注/分类,在给定参数和观测序列(样本)的前提下,使用Viterbi算法进行标记的预测。
标记序列y要求链状,但x无要求,除了一维的词性标注,中文分词,还可以用于离散数据(如用户信息画像),或二维数据(如图像分隔) 等。
缺点:有监督学习计算参数、参数估计的速度慢。




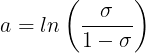
![\large logit(p)=log\frac{p}{1-p}=log\frac{h_\theta(x)}{1-h_\theta(x)}=log\left [ \frac{\frac{1}{1+e^{-\theta^Tx}}}{\frac{e^{-\theta^Tx}}{1+e^{-\theta^Tx}}} \right ]=\theta^Tx](http://img.e-com-net.com/image/info8/0dfb7c43d1c94dde9486efcfb426ddf2.gif)