【论文精读】使用深度卷积神经场从单目图像学习深度

Paper Information

论文：Learning depth from single monocular images using deep convolutional neural fields, F. Liu, C. Shen, G. Lin, I. Reid. IEEE Transactions on Pattern Analysis and Machine Intelligence (TPAMI), 2016.
相关： Deep convolutional neural fields for depth estimation from a single image.F. Liu, C. Shen, G. Lin. Proc. IEEE Conference on Computer Vision and Pattern Recognition (CVPR’15), 2015.
注意：除非另有说明，否则本篇论文使用粗体大写和小写字母分别表示矩阵和列向量。
参考：论文笔记_S2D.37-2015-TPAMI_使用深度卷积神经场从单目图像学习深度 - 惊鸿一博
参考：论文笔记_S2D. 34-2015-CVPR_从单张图像进行深度估计的深度卷积神经场 - 惊鸿一博
注意：除非另有说明，我们使用粗体大写字母和小写字母分别表示矩阵和列向量；0表示所有元素都为0的列向量。

Abstract

在本文中，我们解决了根据单眼图像进行深度估计的问题。与使用多个图像（如立体深度感知）的深度估计相比，单眼图像的深度更具挑战性。先验工作通常着重于利用几何先验或其他信息源，其中大多数使用手工制作的功能。最近，越来越多的证据表明，深度卷积神经网络（CNN）的功能为各种视觉应用创造了新记录。另一方面，考虑到深度值的连续特性，深度估计自然可以公式化为连续条件随机场（CRF）学习问题。因此，在这里，我们提出了一种深度卷积神经场模型，用于从单眼图像估计深度，旨在共同探索深层CNN和连续CRF的能力。特别是，我们提出了一种深度结构化的学习方案，该方案可在统一的深度CNN框架中学习连续CRF的一元和二元潜力。然后，我们进一步提出一个基于完全卷积网络的等效模型和一种新颖的超像素合并方法，该方法快约10倍，以加快深度模型中的逐块卷积。使用这种更有效的模型，我们能够设计更深的网络以追求更好的性能。

我们提出的方法可用于一般场景的深度估计，而无需几何先验，也无需注入任何额外信息。在我们的案例中，可以以封闭形式（in a closed form）计算分区函数的积分（the integral of the partition function），以便我们可以精确地求解对数似然最大化。此外，由于存在封闭形式的解决方案，解决用于预测测试图像的深度的推理问题非常有效。在室内和室外场景数据集上的实验表明，该方法优于最新的深度估计方法。

1 Introduction

事实证明，许多具有挑战性的计算机视觉问题都受益于深度信息的合并（仅举几个语义标签[1]，姿势估计[2]）。尽管当今高度发达的深度传感器（例如Microsoft Kinect）已经使RGBD图像的获取负担得起，但是视觉社区中通常评估的大多数视觉数据集仍然是RGB图像。此外，由于强烈的阳光会引起红外干扰并使深度信息变得非常嘈杂，因此户外应用仍依赖LiDAR或其他激光传感器。这引起了对从单个RGB图像估计深度这一主题的广泛研究兴趣。不幸的是，这是一个众所周知的不适定问题（ill-posed），因为一个捕获的图像场景可能对应于许多现实世界场景[3]。

适定问题是指定解满足下面三个要求的问题：① 解是存在的；② 解是唯一的；③ 解连续依赖于定解条件，即解是稳定的。这三个要求中，只要有一个不满足，则称之为不适定问题（ill-posed）。特别地，如果条件③不满足，那么就称为阿达马意义下的不适定问题。

然而，对于人类来说，从单一图像推断潜在的3D结构是毫不费力的，但对于自动计算机视觉系统来说，这仍然是一项具有挑战性的任务，因为没有可靠的线索可以被利用，如视频中的时间信息，立体声通信等。

以往的工作主要集中于

• 执行几何假设，以推断一个房间的[4]、[5]或室外场景[6]的空间布局。这些模型具有固有的限制，即仅建模特定场景结构的限制，因此不适用于一般的场景深度估计。
• 最近，探索了非参数方法[7]，该方法包括候选图像检索，场景对齐，然后使用具有平滑性约束的优化进行深度推断。这是基于这样的假设，即具有语义相似外观的场景在密集对齐时应该具有相似的深度分布。但是，该方法易于在不同的解耦阶段传播错误，并且严重依赖于构建合理大小的图像数据库来执行候选检索。
• 近年来，已经努力整合其他信息源，例如用户注释[8]，语义标签[9]，[1]。在[1]的最新工作中，Ladicky等人证明联合执行深度估计和语义标记可以相互受益。但是，所有这些方法都使用手工制作的功能。

与之前的研究相比，这里我们建议将深度估计表示为一个深度连续条件随机场(CRF)学习问题，而不依赖于任何几何先验或任何额外的信息。CRF[10]是一种流行的用于结构化输出预测的图形化模型。虽然CRF在分类（离散）领域进行了广泛的研究，但对回归（连续）问题的研究较少。连续CRF的先驱工作之一可以归因于[11]，其中它被提出用于文档检索中的全局排序。在一定的约束条件下，通过解析计算配分函数，可以直接求解最大似然优化。从那时起，连续CRF已经成功地应用于解决各种结构化回归问题，如遥感[12]、[13]、图像去噪[13]。基于这些成功，我们建议利用深度值的连续性，对其进行深度估计，并学习深度卷积神经网络(CNN)中的潜在函数。

自Krizhevsky等人的突破性工作[15]以来，近年来见证了深层CNN的繁荣[14]。 CNN功能已经为各种视觉应用创造了新的记录[16]。尽管在分类问题上取得了种种成功，但深度CNN对结构化学习问题（即深度CNN和图形模型的联合训练）的探索较少，这是一个相对较新且尚未很好解决的问题。据我们所知，目前还没有这样的模型被成功地用于深度估计。在这里，我们通过共同探索CNN和连续CRF来弥合这一差距，将这种新方法称为深度卷积神经场（DCNF）。全卷积网络最近被研究用于密集预测问题，例如语义标记[17]，[18]。基于完全卷积网络的模型具有高效训练和预测的优势。我们在这里利用这一进展来加快DCNF模型的训练和预测。

但是，由全卷积模型生成的特征图通常比输入图像大小要小得多。这可能导致训练和预测方面的问题。在训练期间，需要对真实特征图（ground-truth maps）进行下采样，这可能会导致信息丢失，因为小物体可能会消失。在预测中，上采样操作可能会导致对象边界处的性能下降。因此，我们提出了一种新颖的超像素池化方法来解决这个问题。它共同利用了高效的全卷积网络的优势以及超像素在保留对象边界方面的优势。

综上所述，我们重点介绍这项工作的主要贡献如下：

• 我们通过探索CNN和连续CRF，提出了深度卷积神经场（DCNF）模型用于深度估计。考虑到深度值的连续性质，可以解析计算概率密度函数中的分区函数，因此我们可以直接求解对数似然优化而无需任何近似。可以在反向传播训练中精确计算梯度。而且，由于存在封闭形式的解决方案，解决用于预测新图像深度的MAP问题是非常有效的。
• 我们在统一的深度CNN框架中共同学习CRF的一元势能和二元势能，并使用反向传播对其进行了训练。
• 我们提出了一种基于全卷积网络和新颖的超像素池化方法的更快模型，该模型可将速度提高约10倍，同时产生相似的预测精度。使用这个更有效的模型（我们称为DCNF-FCSP），我们能够设计非常深的网络以获得更好的性能。
• 我们证明了所提出的方法在室内和室外场景数据集上都优于深度估计的最新结果。

我们工作的初步结果出现在Liu等人的[19]上。

1.1 Related Work

我们的方法利用了深度网络在图像分类[15]、[20]、目标检测[21]和语义分割[17]、[18]方面的最新进展，用于单视图图像深度估计。下面，我们将简要介绍一下最密切相关的工作。

深度估计传统的方法[22]、[23]、[9]通常将深度估计表示为一个马尔可夫随机场(MRF)学习问题。由于精确的MRF学习和推理一般是棘手的，这些方法大多采用近似方法，如多条件学习(MCL)或粒子信念传播(PBP)。预测一个新图像的深度是低效的，在[23]中大约需要4-5秒，在[9]中甚至需要更长的时间（30秒）。更糟糕的是，这些方法缺乏灵活性，因为[22]、[23]依赖于图像的水平对齐，而[9]需要预先对可用的训练数据进行语义标注。最近，Liu等人[24]提出了一个离散连续的CRF模型，以考虑相邻超像素之间的关系，例如，遮挡。他们还需要使用近似的方法来进行学习和最大的后验(MAP)推理。此外，他们的方法依靠图像检索来获得合理的初始化。相比之下，这里我们提出了一个深度连续的CRF模型，其中我们可以直接求解对数似然优化，而不需要任何近似，因为配分函数可以解析计算。预测一个新图像的深度是高效的，因为存在一个封闭形式的解。此外，我们不注入任何几何先验或任何额外的信息。另一方面，之前的方法[23]、[9]、[7]、[24]、[1]都在其工作中使用了手工制作的特性，如Texton、GIST、SIFT、PHOG、对象库等。相比之下，我们学习深度CNN来构造CRF的一元势能和二元势能。

最近，Eigen等人[3]提出了一种多尺度CNN的深度估计方法，这与我们在这里的工作相似。然而，我们的方法与他们的方法截然不同：他们使用CNN作为一个黑盒，通过卷积直接回归输入图像的深度图；相反，我们使用CRF来明确地建模相邻超像素的关系，并在一个统一的CNN框架中学习势能（一元和二元）。

[25]和[26]最近的工作与我们的工作相关，因为他们也对单个图像进行深度估计。Su等人的[25]的方法涉及一个像我们这样的连续深度优化步骤，它还包含一个一元回归项和一个二元的局部平滑项。然而，这两项工作的重点是已知分割对象的三维重建，而我们的方法的目标是一般场景图像的深度估计。此外，[25]的方法依赖于一个预先构建的输入对象类别的三维形状数据库，而[26]的工作依赖于类特定的对象关键点和对象分割。相反，我们不注入这些先验。

结合CNN和CRF，Farabet等人提出了一个用于场景标记的多尺度CNN框架[27]，该框架使用CRF作为局部细化的后处理步骤。在[28]最近的工作中，Tompson等人提出了一种混合架构，用于联合训练深度CNN和MRF用于人体姿态估计的架构。它们首先分别训练一个一元项和一个空间模型，然后将它们作为一个微调步骤联合学习。在对整个模型进行微调的过程中，他们只是简单地去除配分函数。相比之下，我们的模型执行连续变量预测。由于配分函数是可积的，可以解析计算，我们可以直接求解对数似然优化。此外，在预测过程中，我们有了映射推理问题的封闭解。虽然没有涉及卷积层，但[29]的工作与我们的工作有相似之处，即这两个连续的CRF都使用神经网络来模拟电势。请注意，[29]中的模型并不深，并且只使用了一个隐藏层。目前还不清楚[29]方法是如何解决我们在这里考虑的具有挑战性的深度估计问题。

全卷积网络最近被积极地研究用于密集预测问题，如语义分割[17]、[18]、图像恢复[30]、图像超分辨率[31]、深度估计[3]。为了处理下采样（downsampled）输出问题，插值一般采用[3]，[18]。在[32]中，Sermanet等人提出了一个输入转移和输出交错的技巧，从没有插值的粗输出中产生密集的预测。后来，Long等人[17]提出了一种反卷积（deconvolution）方法，将上采样放入训练机制中，而不是将其作为后处理步骤来应用。Eigen等人在[3]中提出的用于深度估计的CNN模型也存在这种上采样问题——[3]的预测深度图是原始输入图像的1/4分辨率，并丢失了一些边界区域。他们只是使用双线性插值来上采样预测到输入图像的大小。 与现有的方法不同，我们提出了一种新的超像素池化方法来解决这一问题。它共同利用了高效的完全卷积网络的优势和超像素在保持对象边界方面的优势。

2 DEEP CONVOLUTIONAL NEURAL FIELDS

我们在本节中介绍我们的深度估计的深度卷积神经场(DCNF)模型的细节。

2.1 Overview

这里的目标是推断出描绘一般场景的单个图像中每个像素的深度。根据[23]，[9]，[24]的工作，我们共同假设一个图像是由小的均匀区域（超像素 super pixels）组成的，并考虑由定义在超像素上的节点组成的图形模型。每个超像素都由其质心的深度来表示。设x是一个图像，y=[y1，……，yn]>∈Rn是一个连续深度值的向量，对应于x中的所有n个超像素。与传统的CRFs相似，我们用以下密度函数来模拟数据的条件概率分布：

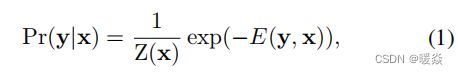
其中E为能量函数，Z为配分函数，定义为：

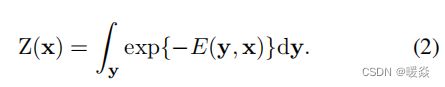
这里，因为y是连续的，所以它是等式中的积分（1）可以在某些情况下进行解析计算，我们将在Sec.2.3中显示。这与需要应用近似方法的离散情况不同。为了预测一个新图像的深度，我们解决了以下最大后验概率（maximum a posteriori，MAP）问题：

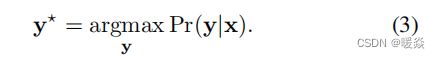
我们将势能函数（energy function）表示为图像x的节点（超像素）N和边缘S上的一元势U（unary potentials）和二元势V（pairwise potentials）的典型组合：

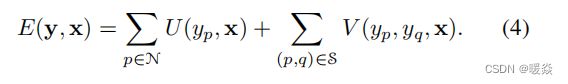
一元项U旨在回归单个超像素的深度值。二元项V鼓励具有相似外观的相邻超像素取取相似的深度。我们的目标是在一个统一的CNN框架中联合学习U和V。

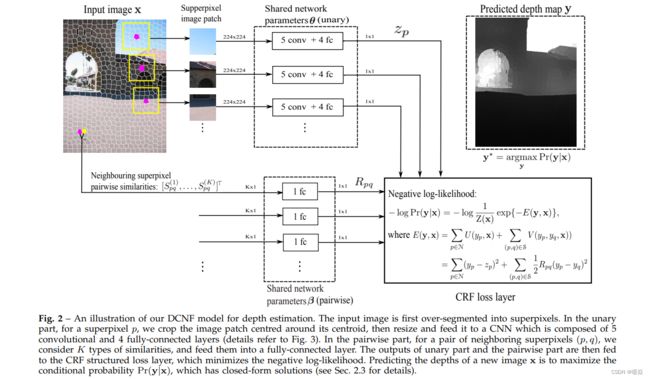
图2绘制了我们用于深度估计的深度卷积神经场模型。

整个网络包括一元部分、二元部分和连续的CRF损耗层。

对于一个被过度分割成n个超像素的输入图像，我们考虑了以每个超像素质心为中心的图像块。然后，一元部分将一个图像块作为输入，并将其输入给一个输出为单一数字的CNN，即超像素的回归深度值。

一元部分的网络由5个卷积层和4个全连接层组成，详见图3。请注意，CNN参数在所有超像素之间共享。

二元部分以所有相邻超像素对的相似度向量(每个有K个分量)作为输入，将每个输入一个全连接层（参数在不同对之间共享），然后输出一个包含每个相邻超像素对的所有一维相似性的向量。

连续的CRF损失层从一元项和两两项中获取输出，以最小化负对数似然。与[3]中的直接回归方法相比，我们的模型具有两个潜在的优势：

• 当我们构造一元势时，我们实现了平移不变性，而不管超像素的坐标（详见2.2）；
• 我们通过成对势明确地模拟相邻超像素的关系。

下面，我们将详细描述等式中能量函数中所涉及的势函数 (4).

2.2 Potential Functions

2.2.1 Unary potential

通过考虑最小二乘损失，由CNN的输出构造出一元势能：

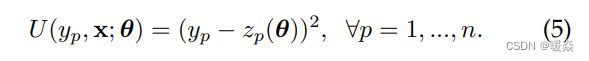
这里z_p是由CNN参数θ参数化的超像素p的回归深度。

一元部分的网络架构如图3所示。我们在图3中的CNN模型主要是受到克里热夫斯基等人[15]著名的网络架构的启发。它由5个卷积层和4个全连接层组成。首先将输入的图像过度分割（over-segmented）成超像素，然后对每个超像素，我们考虑以其质心为中心的图像块。每个图像块被调整到224×224像素（其他分辨率也可以工作），然后输入到卷积神经网络。请注意，卷积层和全连接层在不同超像素的所有图像块中共享。使用校正的线性单元(ReLU)作为五个卷积层和前两个完全连接层的激活函数。对于第三个全连通层，我们使用逻辑函数$f(x)=(1+e^{-1}{)}^{-1}$作为激活函数。最后一个全连接层起着模型集成的作用，后面没有激活函数。输出是单个超像素的一维实值深度。

2.2.2 Pairwise potential

我们从K种类型的相似度观测中构造二元势，每一种观测都通过利用相邻超像素的一致性信息来增强平滑性：

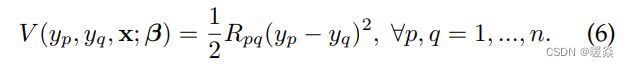
这里的$R_{pq}$是来自相邻超像素对(p，q)的成对部分（见图2）的网络输出。我们在这里使用了一个全连接的图层：

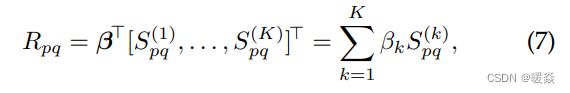
其中，$S^{(k)}$是第k个相似度矩阵，其元素为$S_{pq}^{(k)}$（$S^{(k)}$是对称的）；$\beta =[{\beta }_1，\dots \dots ，{\beta }_k{]}^T$是网络参数。从等式开始（7），我们可以看到我们没有使用任何激活函数。然而，由于我们的框架是通用的，更复杂的网络可以无缝地合并为成对的部分。在第二节中2.3，我们将证明我们可以推导出计算关于β的梯度的一般形式(见等式 (19))，以确保在等式中的Z(x)（2）是可积的，在[11]中我们需要${\beta }_k\ge 0$。请注意，这是一个充分的条件，但不是必要的条件。

这里我们考虑3种类型的成对相似性，通过颜色差异，颜色直方图差异和纹理差异的局部二进制模式(LBP)[33]，采用传统形式：

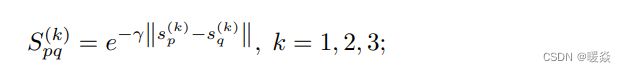
其中，$S_p^{(k)}$、$S_q^{(k)}$为由颜色、颜色直方图和LBP计算得到的超像素p、q的观测值；||·||表示一个向量的L2范数，γ为一个常数。它也可以学习成对项的特征。例如，二元项可以是一个以原始像素作为输入的深度CNN。一个更复杂的成对能量可以进一步改进估计，特别是对于复杂的离散标签问题，以增加计算复杂性的代价。对于深度估计，我们发现我们目前的成对能量已经工作得很好。

2.3 Learning

2.4 Speeding up training using fully convolutional networks and superpixel pooling

到目前为止，我们已经提出了基于图像超像素的深度估计的DCNF模型。从图2中，我们可以看到，为了构造一元势，我们本质上是在执行块卷积（patchwise convolutions）(在R-CNN[21]中执行类似的操作)。该方法的一个主要关注点是它的计算效率和内存消耗，因为我们需要对单个输入图像执行超过数百甚至数千个（超像素数）的图像块的卷积。由于显著的图像块重叠（image patch overlaps），许多这些卷积是冗余的。
自然地，减少计算负担的一个有希望的方向是对整个图像进行一次卷积，然后得到每个超像素的卷积特征。然而，要从所得到的卷积映射中找到图像超像素的卷积特征，就需要建立这两者之间的关联。因此，我们在此提出了一个改进的模型，我们称之为DCNF-FCSP（带有全卷积网络和超像素池的DCNF），基于全卷积网络和一种新的超像素池方法，来解决这个问题。正如我们将在3.2中展示的那样，该新模型显著提高了训练和预测的速度，同时产生了几乎相同的预测精度。最重要的是，有了这个更高效的模型，我们就能够设计出更深层次的网络来实现更好的性能。

pixel-wise，patch-wise，image-wise的含义如下：

pixel-wise 素级别，一张图片是由一个个图像基本单位pixel组成。
image-wise 图像级别，比如一张图片的标签是狗，是对整个图片的标注。
patch-wise 块级别，介于像素级别和图像级别的区域，每个patch都是由好多个pixel组成的。

2.4.1 DCNF-FCSP overview

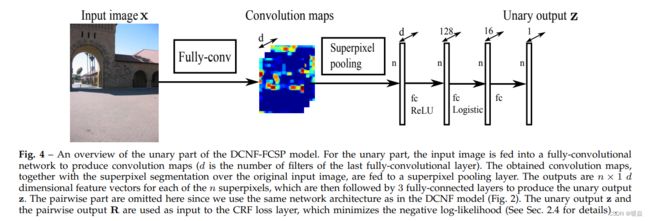
与DCNF模型相比，我们的新DCNF-FCSP模型主要改进了一元部分，同时保持了与图2相同的成对网络结构。我们在图4中展示了一元部分的模型体系结构。具体来说，输入的图像被输入到一个完全卷积的网络（在后面介绍）。输出为大小为$h\times w\times d$的卷积特征图（d为得到的卷积特征向量的维数，即最后一个卷积层的信道数）。卷积映射的大小h×w通常小于输入图像的大小。输出卷积映射中的每个卷积特征向量都对应于输入图像中的一个图像块。我们提出了一种新的超像素池化方法（如下所述），将这些输出与输入图像中的超像素关联起来。具体来说，将卷积特征映射作为超像素池化层的输入，得到n个具有d个维数的超像素特征向量（n为超像素数）。然后将超像素特征向量输入到3个完全连通的层中，产生一元输出z。我们使用如图2所示的相同的成对网络架构，但我们在这里没有显示。利用一元输出z和成对输出R，根据方程式构造势函数（5）和（6），并优化负对数似然值。

与原来提出的DCNF方法相比，这种改进的DCNF-FCSP模型只需要对整个图像进行一次卷积，而不是数百个超像素图像块。这大大减少了计算和GPU内存负担，带来了大约10倍的训练加速，同时产生了几乎相同的预测精度，正如我们在后面的3.2章节中演示的那样。接下来，我们将详细介绍全卷积网络和超像素池化方法。

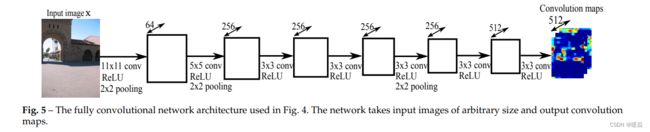
2.4.2 Fully convolutional networks

典型的CNN模型，包括AlexNet[15]、vggNet[34]、[20]等，都是由卷积层和全连接层组成的。它们通常以标准大小的图像作为输入，例如，224×224像素，以产生非空间（nonspatial）输出。相比之下，一个完全卷积的网络可以将任意大小的图像作为输入，并输出卷积的空间映射。因此，最近人们对密集预测问题[17]、[18]、[31]、[3]进行了积极的研究。我们在这里利用CNN的这种新的发展趋势来加速DCNF模型中的块卷积。我们举例说明了我们在图5中使用的全卷积网络架构。如图所示，网络由7个卷积层组成，前5个层从AlexNet[15]转移。然后我们添加2个卷积层，3×3滤波器大小和512个通道。该网络采用任意大小的输入图像，输出通道d=512的卷积图。请注意，我们可以在这里设计更深层次的网络，以追求更好的性能。我们将在3.3小节中进行演示。使用更深层次的模型的好处。

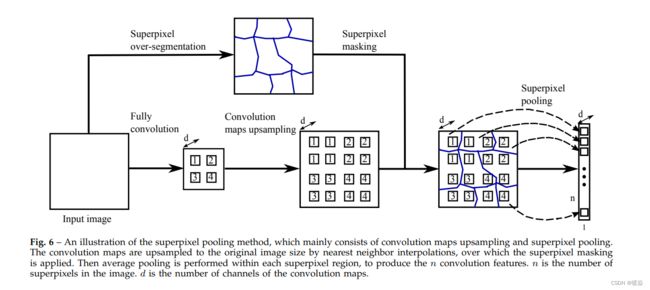
2.4.3 Superpixel pooling

输入图像经过全卷积网络后，得到卷积映射。为了获得超像素特征，我们需要将这些卷积特征映射与图像的超像素关联起来。因此，我们提出了一种新的超像素池化方法。该方法如图6所示，主要由卷积图上采样和超像素平均池化组成。通常，这个超像素池化层将卷积映射作为输入和输出超像素特征。具体地说，所得到的卷积映射首先通过最近邻插值上采样到原始图像的大小。请注意，其他的插值方法，如线性插值，也可能适用。然而，如下所讨论的，最近邻插值使实现更容易，计算更快。

然后应用超像素掩蔽，并在每个超像素区域内进行平均池化。输出是汇集的超像素特征，用于构造一元势。在之后的介绍中，我们将详细描述这种方法。

【待补充】

到目前为止，我们已经成功地建立了卷积特征图和图像超像素之间的关联。值得注意的是，虽然提出的超像素池方法虽然简单，但它共同利用了完全卷积网络和超像素的优点。它为DCNF模型中使用的块卷积提供了一种有效但同样有效的方法，正如我们在Sec3.2中所演示的那样。

2.5 Implementation details

我们基于CNN工具箱：VLFeatMatConNovNet1进行了自己的修改。培训是在标准桌面上完成的，使用NVIDIAGTX780GPU，6GB内存。DCNF模型，采用图3中的网络设计，大约有4000万个参数。DCNF-FCSP模型，采用图5中的网络设计，有约580万个参数。由于具有非常深的网络架构，DCNF-FCSP模型有大约2000万个参数。DCNF模型的大量参数主要来自图3中的4096全连接层，在DCNF-FCSP模型中去掉。接下来，我们将在下面介绍这所提出的两个模型的实现细节

DCNF：我们使用[34]在ImageNet上训练的CNN模型初始化图3中一元部分的前6层。首先，我们不会通过保持前6层的固定来反向传播，并通过以下设置训练网络的其余部分（我们将这个过程称为预训练）：动量设置为0.9，权重衰减参数λ1，λ2设置为0.0005。在训练前，学习速率初始化为0.0001，每20个周期降低40%。然后我们运行了60个运动周期来报告训练前的结果（学习率下降了两次）。在训练前，一个网络前传进行深度预测所需的时间少于0.1秒。然后，我们用相同的动量和权值衰减来训练整个网络。在Make3D数据集上训练整个网络大约需要16.5个小时，在NYUv2数据集上大约需要33个小时。对于这个微调模型，它需要∼1.1s来进行深度预测。

DCNF-FCSP：我们用在[34]的ImageNet上训练的相同模型初始化图5中的前5层。动量和权重衰减参数的设置与DCNF模型中的相同。我们还使用了与DCNF模型中相同的训练协议，即首先进行预训练，然后对整个模型进行微调。

3 EXPERIMENTS

【待补充】

3.1 Baseline comparisons

为了证明该方法的有效性，我们首先对几个基线方法进行了实验比较：

• SVR：我们使用图3前6层的CNN表示训练支持向量回归器；
• SVR（smooth）：我们通过解决等式中的推理问题，在经过训练的SVR预测中添加一个平滑项 (22).由于对多个成对参数进行调整并不简单，我们只使用色差作为成对势，并在验证集上手动调整选择参数β；
• Unary only：我们将图2中的CRF损失层替换为最小二乘回归层(通过设置成对输出R_pq=0，p，q=1，…，n)，它退化为SGD训练的深度回归模型。
• Unary only（smooth）：我们在我们的统一模型中添加类似的平滑项，就像在SVR（平滑）情况中所做的那样。

3.1.1 NYU v2 data

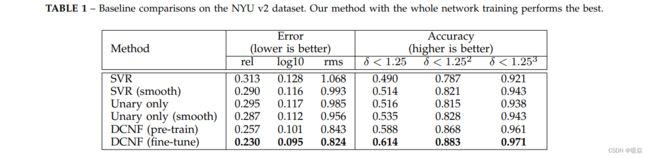
NYUv2数据集由1449张室内场景的RGBD图像组成，其中795张用于训练，654张用于测试（我们使用数据集提供的标准训练/测试分割）。我们在表1中报告了基线比较。从表中可以得出几个结论：

1)仅用一元项训练时，深层网络有利于更好的性能，这表明我们的一元模型优于SVR模型；
2)在SVR或一元模型中添加平滑项有助于提高预测精度；
3)我们的DCNF模型在统一的深度CNN框架中联合学习一元参数和两两参数，取得了最好的性能。

此外，对整个网络进行微调还可以进一步提高性能。这些都很好地证明了我们的模型的有效性。

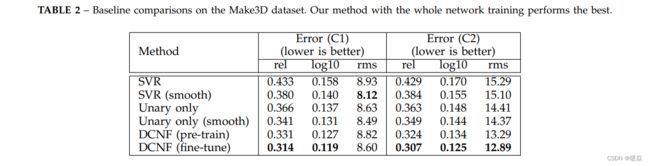
3.1.2 Make3D data

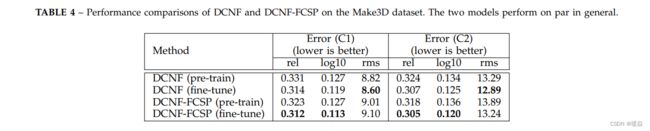
Make3D数据集包含534幅描绘户外场景的图像，其中400张用于训练，134张图像用于测试。正如在[23]，[24]中指出的，这个数据集有局限性：深度的最大值是81米，遥远的物体都被映射到81米的一个距离。作为一种补救措施，在[24]中使用了两个标准来报告预测误差：(C1)误差仅在地面真实深度小于70米的区域进行计算；(C2)计算整个图像的误差。我们按照此方案报告了表2中的评估结果。正如我们所看到的，我们的全网络训练的全DCNF模型在所有比较的基线方法中表现最好。使用更深层次的网络和添加平滑度术语通常有助于提高性能。

3.2 DCNF vs. DCNF-FCSP

在本节中，我们比较了所提出的DCNF和DCNF-FCSP在预测精度和计算效率方面的性能。比较的预测性能见表3和表4。我们可以看到，所提出的DCNF-FCSP模型执行得非常接近于DCNF模型。接下来，我们比较了这两种模型的计算效率。具体来说，我们报告了每个图像使用的不同超像素数的整个模型的训练时间（网络前向+向后）。在NYUv2数据集上进行了比较，如图11所示。结果证明，DCNF-FCSP模型通常比DCNF模型快数量级。此外，随着超像素数量的增加，加速速度更加显著。我们还比较了整个模型在深度预测过程中的网络正向时间，并将结果绘制在图12中。所示的时间是处理一个图像。我们可以看到，DCNF-FCSP模型比DCNF模型要快得多，也更有可扩展性。最重要的是，有了这个更高效的dcnffcsp模型，我们可以设计更深层次的网络以获得更好的性能，正如我们将在3.3中展示的那样。

3.3 State-of-the-art comparisons

3.3.1 NYU v2 data

3.3.2 Make3D data

3.3.3 KITTI data

4 CONCLUSION

我们提出了一个基于单一图像的深度估计的深度卷积神经场模型。该方法将深度CNN和连续CRF的强度结合在一个统一的CNN框架中。我们证明了对数似然优化在我们的方法中可以直接解决使用反向传播，而不需要任何近似。通过求解映射推理，可以有效地预测新图像的深度。我们进一步提出了一种基于全卷积网络的改进模型和一种新的超像素池化方法。我们的实验证明，它同样有效，同时带来数量级更快的训练加速，这使使用更深的网络更好的性能。实验结果表明，该方法在室内和室外场景数据集上均优于现有的实验方法。

我们的方法的主要局限性是它没有利用任何几何线索，这可以在未来的工作中进行探索。鉴于我们的方法的一般学习框架，它也可以应用于其他视觉应用与最小的修改，例如，图像去噪，和去模糊。另一个潜在的工作方向是将我们的深度估计模型应用于有利于其他视觉任务，例如，语义分割，目标检测，在传统的没有地面真实深度的视觉数据集上。

REFERENCES

[1] L. Ladick, J. Shi, and M. Pollefeys, “Pulling things out of perspective,” in Proc. IEEE Conf. Comp. Vis. Patt. Recogn., 2014.
[2] J. Shotton, R. B. Girshick, A. W. Fitzgibbon, T. Sharp, M. Cook, M. Finocchio, R. Moore, P. Kohli, A. Criminisi, A. Kipman, and A. Blake, “Efficient human pose estimation from single depth images,” IEEE Trans. Pattern Anal. Mach. Intell., 2013.
[3] D. Eigen, C. Puhrsch, and R. Fergus, “Depth map prediction from a single image using a multi-scale deep network,” in Proc. Adv. Neural Inf. Process. Syst., 2014.
[4] V. Hedau, D. Hoiem, and D. A. Forsyth, “Thinking inside the box: Using appearance models and context based on room geometry,” in Proc. Eur. Conf. Comp. Vis., 2010.
[5] D. C. Lee, A. Gupta, M. Hebert, and T. Kanade, “Estimating spatial layout of rooms using volumetric reasoning about objects and surfaces,” in Proc. Adv. Neural Inf. Process. Syst., 2010.
[6] A. Gupta, A. A. Efros, and M. Hebert, “Blocks world revisited: Image understanding using qualitative geometry and mechanics,” in Proc. Eur. Conf. Comp. Vis., 2010.
[7] K. Karsch, C. Liu, and S. B. Kang, “Depthtransfer: Depth extraction from video using non-parametric sampling,” IEEE Trans. Pattern Anal. Mach. Intell., 2014.
[8] B. C. Russell and A. Torralba, “Building a database of 3d scenes from user annotations,” in Proc. IEEE Conf. Comp. Vis. Patt. Recogn., 2009.
[9] B. Liu, S. Gould, and D. Koller, “Single image depth estimation from predicted semantic labels,” in Proc. IEEE Conf. Comp. Vis. Patt. Recogn., 2010.
[10] J. D. Lafferty, A. McCallum, and F. C. N. Pereira, “Conditional random fields: Probabilistic models for segmenting and labeling sequence data,” in Proc. Int. Conf. Mach. Learn., 2001.
[11] T. Qin, T.-Y. Liu, X.-D. Zhang, D.-S. Wang, and H. Li, “Global ranking using continuous conditional random fields,” in Proc. Adv. Neural Inf. Process. Syst., 2008.
[12] V. Radosavljevic, S. Vucetic, and Z. Obradovic, “Continuous conditional random fields for regression in remote sensing,” in Proc. Eur. Conf. Artificial Intell., 2010.
[13] K. Ristovski, V. Radosavljevic, S. Vucetic, and Z. Obradovic, “Continuous conditional random fields for efficient regression in large fully connected graphs,” in AAAI Conf. Artificial Intell., 2013.
[14] Y. LeCun, B. Boser, J. S. Denker, D. Henderson, R. E. Howard, W. Hubbard, and L. D. Jackel, “Backpropagation applied to handwritten zip code recognition,” Neural Comput., 1989.
[15] A. Krizhevsky, I. Sutskever, and G. E. Hinton, “ImageNet classification with deep convolutional neural networks,” in Proc. Adv. Neural Inf. Process. Syst., 2012.
[16] A. Sharif Razavian, H. Azizpour, J. Sullivan, and S. Carlsson, “CNN features off-the-shelf: An astounding baseline for recognition,” in Proc. IEEE Conf. Comput. Vis. & Pattern Recogn. Workshops, June 2014.
[17] J. Long, E. Shelhamer, and T. Darrell, “Fully convolutional networks for semantic segmentation,” in Proc. IEEE Conf. Comp. Vis. Patt. Recogn., 2015.
[18] M. Cogswell, X. Lin, S. Purushwalkam, and D. Batra, “Combining the best of graphical models and convnets for semantic segmentation,” 2014. [Online]. Available: http://arxiv.org/abs/1412.4313
[19] F. Liu, C. Shen, and G. Lin, “Deep convolutional neural fields for depth estimation from a single image,” in Proc. IEEE Conf. Comp. Vis. Patt. Recogn., 2015.
[20] K. Simonyan and A. Zisserman, “Very deep convolutional networks for large-scale image recognition,” in Proc. Int. Conf. Learn. Representations, 2015.
[21] R. Girshick, J. Donahue, T. Darrell, and J. Malik, “Rich feature hierarchies for accurate object detection and semantic segmentation,” in Proc. IEEE Conf. Comp. Vis. Patt. Recogn., 2014.
[22] A. Saxena, S. H. Chung, and A. Y. Ng, “Learning depth from single monocular images,” in Proc. Adv. Neural Inf. Process. Syst., 2005.
[23] A. Saxena, M. Sun, and A. Y. Ng, “Make3D: Learning 3d scene structure from a single still image,” IEEE Trans. Pattern Anal. Mach.
Intell., 2009.
[24] M. Liu, M. Salzmann, and X. He, “Discrete-continuous depth estimation from a single image,” in Proc. IEEE Conf. Comp. Vis. Patt. Recogn., 2014.
[25] H. Su, Q. Huang, N. J. Mitra, Y. Li, and L. Guibas, “Estimating image depth using shape collections,” ACM Trans. Graph., 2014.
[26] A. Kar, S. Tulsiani, J. Carreira, and J. Malik, “Category-specific object reconstruction from a single image,” in Proc. IEEE Conf. Comp. Vis. Patt. Recogn., June 2015.
[27] C. Farabet, C. Couprie, L. Najman, and Y. LeCun, “Learning hierarchical features for scene labeling,” IEEE Trans. Pattern Anal. Mach. Intell., 2013.
[28] J. Tompson, A. Jain, Y. LeCun, and C. Bregler, “Joint training of a convolutional network and a graphical model for human pose estimation,” in Proc. Adv. Neural Inf. Process. Syst., 2014.
[29] T. Baltruˇsaitis, L.-P. Morency, and P. Robinson, “Continuous conditional neural fields for structured regression,” in Proc. Eur. Conf.
Comp. Vis., 2014.
[30] D. Eigen, D. Krishnan, and R. Fergus, “Restoring an image taken through a window covered with dirt or rain,” in Proc. IEEE Int.
Conf. Comp. Vis., 2013.
[31] C. Dong, C. C. Loy, K. He, and X. Tang, “Learning a deep convolutional network for image super-resolution,” in Proc. Eur. Conf. Comp. Vis., 2014.
[32] P. Sermanet, D. Eigen, X. Zhang, M. Mathieu, R. Fergus, and Y. LeCun, “OverFeat: Integrated recognition, localization and detection using convolutional networks,” in Proc. Int. Conf. Learn. Representations, 2014.
[33] T. Ojala, M. Pietikainen, and D. Harwood, “Performance evaluation of texture measures with classification based on kullback discrimination of distributions,” in Proc. IEEE Int. Conf. Patt. Recogn., 1994.
[34] K. Chatfield, K. Simonyan, A. Vedaldi, and A. Zisserman, “Return of the devil in the details: Delving deep into convolutional nets,” in Proc. British Machine Vis. Conf., 2014.
[35] P. K. Nathan Silberman, Derek Hoiem and R. Fergus, “Indoor segmentation and support inference from RGBD images,” in Proc. Eur. Conf. Comp. Vis., 2012.
[36] A. Geiger, P. Lenz, C. Stiller, and R. Urtasun, “Vision meets robotics: The KITTI dataset,” Int. J. Robotics Res., 2013.
[37] R. Achanta, A. Shaji, K. Smith, A. Lucchi, P. Fua, and S. S ¨usstrunk, “SLIC superpixels compared to state-of-the-art superpixel methods,” IEEE Trans. Pattern Anal. Mach. Intell., 2012.
[38] F. Durand and J. Dorsey, “Fast bilateral filtering for the display of high-dynamic-range images,” ACM Trans. Graph., 2002.
[39] C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed, D. Anguelov, D. Erhan, V. Vanhoucke, and A. Rabinovich, “Going deeper with
convolutions,” in Proc. IEEE Conf. Comp. Vis. Patt. Recogn., 2015.