机器学习之逻辑回归（实战源码）

1.分类问题介绍

任务：输入：电子邮件；

           输出：此邮件为垃圾文件/普通邮件

流程：

• 标注样本邮件是垃圾邮件还是普通邮件
• 获取批量的样本邮件及其标签，学习其特征（计算机实现）
• 针对新邮件，自动判断其类别

特征：用于帮助判断是否为垃圾邮件的属性

• 发件人包含:%&*...
• 正文包含：现金，领取等

分类：

1. 定义：根据已知样本的某些特征，判断一个新样本属于哪一类别。
2. 基本框架：y=f(x1,x2.....xn)，判断类别为N，如果y = N
3. 方法

• 逻辑回归：建立逻辑回归方程，判断类别
• KNN近邻模型
• 决策树
• 神经网络

分类任务与回归任务的区别：

分类目标：判断类别      模型输出：非连续型标签

回归目标：建立函数关系   模型输出：连续性数值

 2.逻辑回归：

可以用线性回归进行预测，但当样本数据很大时，效果不好。可以将单位跃阶函数换为对数几率函数P(X)。

逻辑回归是用于解决分类问题的一种模型，根据数据特征或属性，计算其属于哪一类别的概率P(X)，根据概率数值判断其所属类别。主要应用场景：二分类问题。

对数几率函数：        

单位跃阶函数：y = 1, P(X)>=0.5      

                         y = 0, P(X)<0.5. 其中y为类别结果，P为概率分布函数，x为特征值。

注：若输入为多维度，将x换成一个函数即可。这里以二维为例：

  ,  其中，称为决策边界。

逻辑回归结合多项式边界函数可解决复杂的分类问题。

逻辑回归求解：

• 根据训练样本，寻决策类边界，即寻找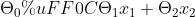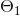，...的过程。
• 线性回归求解时，最小化损失函数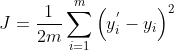。但分类问题中，标签和预测结果都是离散点，使用该损失函数无法寻找极小值点。所以我们将损失函数变为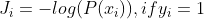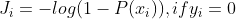，，为了方便计算，化为。
• 此时，逻辑回归的求解目标为：min(J()).
• 线性回归时，用梯度下降法：J=f(P)----->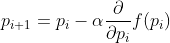。在这里我们可以将一下两步重复至收敛：

1. 
2. 

3.实战准备

（1）分类散点图可视化

• 未区分类别散点图：

plt.scatter(x1,x2)

• 区分类别散点图：

  #mask筛选数据类别，1：true
  mask = y == 1
  #将y==1的类别选出来并画出来，圆形
  passed = plt.scatter(x1[mask],x2[mask])
  #mask取反，画出0的，用三角形^
  failed = plt.scatter(x1[~mask],x2[~mask],marker='^')

  （2）模型训练：

  from sklearn.linear_model import LogisticRegression
  Ir_model = LogisticRegression()
  Ir_model.fit(x,y)

  （3）边界函数系数：

  theta1,theta2 = LR.coef_[0][0],LR.coef_[0][1]
  theta0 = LR.intercept_[0]

  （4）对新数据做预测：

  predictions = Ir_model.predict(x_new)

  （5）生成新的属性数据：（将直线变成曲线）

  #增加三列数据
  x1_2 = x1*x1;
  x2_2 = x2*x2;
  x1_x2 = x1*x2;
  X_new_dic = {'x1':x1,'x2':x2,'x1^2':x1_2,'x2^2':x2_2,'x1x2':x1_x2}
  X_new = pd.DataFrame(X_new_dic)

  （6）计算准确率：

  from sklearn.metrics import accuracy_score
  y_predict = LR.predict(X)
  accuracy = accuracy_score(y,y_predict)
  
  
  #也可以通过画图看决策边界效果，可视化模型表现
  plt.plot(x1,x1_boundary)
  passed = plt.scatter(x1[mask],x2[mask])
  failed = plt.scatter(x1[~mask],x2[~mask],marker='^')

  4.实例1：给定第一次和第二次考试的分数，判断第三次考试能否通过。

#load the data
import pandas as pd
import numpy as np
data = pd.read_csv('examdata.csv')

#visualize the data
#展示数据
%matplotlib inline
from matplotlib import pyplot as plt
fig1 = plt.figure()
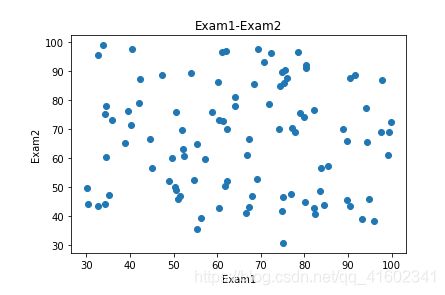
plt.scatter(data.loc[:,'Exam1'],data.loc[:,'Exam2'])
plt.title('Exam1-Exam2')
plt.xlabel('Exam1')
plt.ylabel('Exam2')
plt.show()

 

#add label mask
mask = data.loc[:,'Pass'] == 1

fig2 = plt.figure()
passed = plt.scatter(data.loc[:,'Exam1'][mask],data.loc[:,'Exam2'][mask])
failed = plt.scatter(data.loc[:,'Exam1'][~mask],data.loc[:,'Exam2'][~mask])
plt.title('Exam1-Exam2')
plt.xlabel('Exam1')
plt.ylabel('Exam2')
#加题注
plt.legend((passed,failed),('passed','failed'))
plt.show()

 

#define x y
#去除pass这一列
X = data.drop(['Pass'],axis = 1)
#y为最后一列
y = data.loc[:,'Pass']
X1 = data.loc[:,'Exam1']
X2 = data.loc[:,'Exam2']

#establish the model and train it
from sklearn.linear_model import LogisticRegression
LR = LogisticRegression()
LR.fit(X,y)

#show the predicted result and its accuray
y_predict = LR.predict(X)
print(y_predict)

from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y,y_predict)
print(accuracy)

#Exam1 = 70 Exam2 = 65
y_test = LR.predict([[70,65]])
print('passed' if y_test == 1 else 'failed')

theta0 = LR.intercept_
theta1,theta2 = LR.coef_[0][0],LR.coef_[0][1]
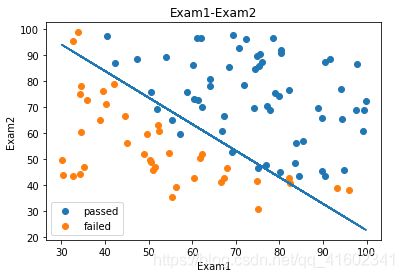
print(theta0,theta1,theta2)

X2_new = -(theta0 +theta1*X1)/theta2

fig2 = plt.figure()
passed = plt.scatter(data.loc[:,'Exam1'][mask],data.loc[:,'Exam2'][mask])
failed = plt.scatter(data.loc[:,'Exam1'][~mask],data.loc[:,'Exam2'][~mask])
plt.plot(X1,X2_new)
plt.title('Exam1-Exam2')
plt.xlabel('Exam1')
plt.ylabel('Exam2')
#加题注
plt.legend((passed,failed),('passed','failed'))
plt.show()

#create new data
X1_2 = X1 * X1
X2_2 = X2 * X2
X1_X2 = X1 * X2
X_new = {'X1':X1,'X2':X2,'X1_2':X1_2,'X2_2':X2_2,'X1_X2':X1_X2}
X_new = pd.DataFrame(X_new)

#establish new model and train
LR2 = LogisticRegression()
LR2.fit(X_new,y)

y2_predict = LR2.predict(X_new)
accuracy2 = accuracy_score(y,y2_predict)

#给X1排序，不然画出的图形是好多条线
X1_new = X1.sort_values()

theta0 = LR2.intercept_
theta1,theta2,theta3,theta4,theta5 = LR2.coef_[0][0],LR2.coef_[0][1],LR2.coef_[0][2],LR2.coef_[0][3],LR2.coef_[0][4],
a = theta4
b = theta5 * X1_new + theta2
c = theta0 + theta1 * X1_new + theta3 * X1_new * X1_new
X2_new_boundary = (-b + np.sqrt(b * b - 4 * a * c))/(2 * a)
#print(theta0,theta1,theta2,theta3,theta4,theta5)

fig3 = plt.figure()
passed = plt.scatter(data.loc[:,'Exam1'][mask],data.loc[:,'Exam2'][mask])
failed = plt.scatter(data.loc[:,'Exam1'][~mask],data.loc[:,'Exam2'][~mask])
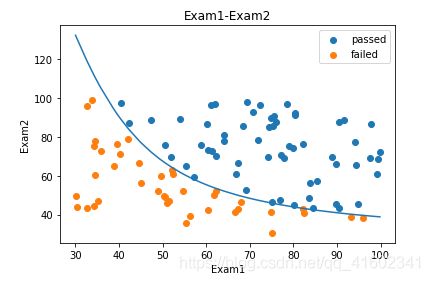
plt.plot(X1_new,X2_new_boundary)
plt.title('Exam1-Exam2')
plt.xlabel('Exam1')
plt.ylabel('Exam2')
#加题注
plt.legend((passed,failed),('passed','failed'))
plt.show()

5.实例2：芯片质量检测。这个def 了一个函数来直接调用实现。

#load the data
import pandas as pd
import numpy as np
data = pd.read_csv('chip_test.csv')

#add label mask
mask = data.loc[:,'pass'] == 1

#visualize the data 
%matplotlib inline
from matplotlib import pyplot as plt
fig = plt.figure()
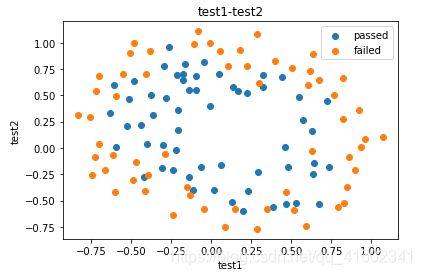
passed = plt.scatter(data.loc[:,'test1'][mask],data.loc[:,'test2'][mask])
failed = plt.scatter(data.loc[:,'test1'][~mask],data.loc[:,'test2'][~mask])
plt.title('test1-test2')
plt.xlabel('test1')
plt.ylabel('test2')
plt.legend((passed,failed),('passed','failed'))
plt.show()

#define x y
X = data.drop(['pass'],axis = 1)
y = data.loc[:,'pass']
X1 = data.loc[:,'test1']
X2 = data.loc[:,'test2']
#creat new data
X1_2 = X1 * X1
X2_2 = X2 * X2
X1_X2 = X1 * X2
X_new = {'X1':X1,'X2':X2,'X1_2':X1_2,'X2_2':X2_2,'X1_X2':X1_X2}
X_new = pd.DataFrame(X_new)

#establish the model and train
from sklearn.linear_model import LogisticRegression
LR = LogisticRegression()
LR.fit(X_new,y)

from sklearn.metrics import accuracy_score
y_predict = LR.predict(X_new)
accuracy = accuracy_score(y,y_predict)
print(accuracy)

#原始方法
X1_new = X1.sort_values()
theta0 = LR.intercept_
theta1,theta2,theta3,theta4,theta5 = LR.coef_[0][0],LR.coef_[0][1],LR.coef_[0][2],LR.coef_[0][3],LR.coef_[0][4],
a = theta4
b = theta5 * X1_new + theta2
c = theta0 + theta1 * X1_new + theta3 * X1_new * X1_new
X2_new_boundary = (-b + np.sqrt(b * b - 4 * a * c))/(2 * a)

fig3 = plt.figure()
passed = plt.scatter(data.loc[:,'test1'][mask],data.loc[:,'test2'][mask])
failed = plt.scatter(data.loc[:,'test1'][~mask],data.loc[:,'test2'][~mask])
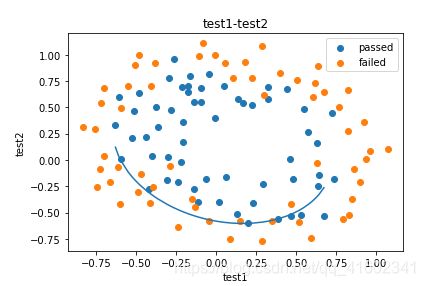
plt.plot(X1_new,X2_new_boundary)
plt.title('test1-test2')
plt.xlabel('test1')
plt.ylabel('test2')
#加题注
plt.legend((passed,failed),('passed','failed'))
plt.show()

#新方法define f(x)
def f(x):
    a = theta4
    b = theta5 * x + theta2
    c = theta0 + theta1 * x + theta3 * x * x
    X2_new_boundary1 = (-b + np.sqrt(b * b - 4 * a * c))/(2 * a)
    X2_new_boundary2 = (-b - np.sqrt(b * b - 4 * a * c))/(2 * a)
    return X2_new_boundary1,X2_new_boundary2

X2_new_boundary1 = []
X2_new_boundary2 = []
for x in X1_new:
    X2_new_boundary1.append(f(x)[0])
    X2_new_boundary2.append(f(x)[1])

fig4 = plt.figure()
passed = plt.scatter(data.loc[:,'test1'][mask],data.loc[:,'test2'][mask])
failed = plt.scatter(data.loc[:,'test1'][~mask],data.loc[:,'test2'][~mask])
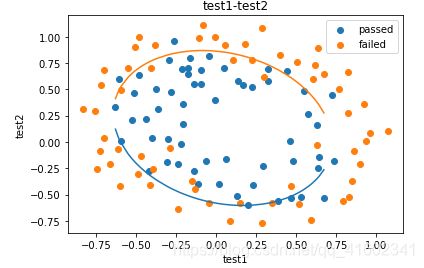
plt.plot(X1_new,X2_new_boundary1)
plt.plot(X1_new,X2_new_boundary2)
plt.title('test1-test2')
plt.xlabel('test1')
plt.ylabel('test2')
#加题注
plt.legend((passed,failed),('passed','failed'))
plt.show()

X1_range = [-0.9 + x/10000 for x in range(0,19000)]
X1_range = np.array(X1_range)
X2_new_boundary1 = []
X2_new_boundary2 = []
for x in X1_range:
    X2_new_boundary1.append(f(x)[0])
    X2_new_boundary2.append(f(x)[1])

fig5 = plt.figure()
passed = plt.scatter(data.loc[:,'test1'][mask],data.loc[:,'test2'][mask])
failed = plt.scatter(data.loc[:,'test1'][~mask],data.loc[:,'test2'][~mask])
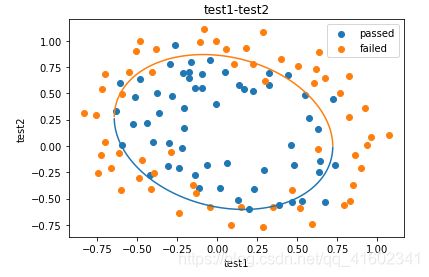
plt.plot(X1_range,X2_new_boundary1)
plt.plot(X1_range,X2_new_boundary2)
plt.title('test1-test2')
plt.xlabel('test1')
plt.ylabel('test2')
#加题注
plt.legend((passed,failed),('passed','failed'))
plt.show()