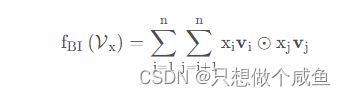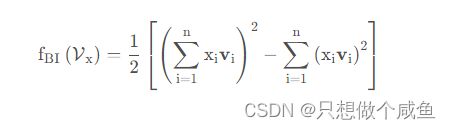NFM(Neural Factorization Machines)：模型原理及pytorch代码实现

一、前言

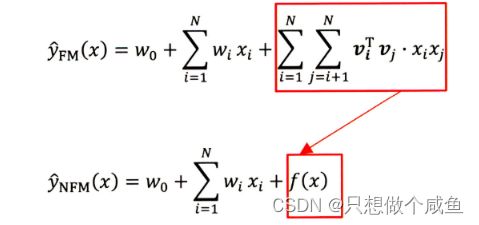
FM已经公认是稀疏数据预测中最有效的嵌入方法之一，真实世界中的数据往往是非线性且内部结构复杂，而FM虽然能够比较好的处理稀疏数据， 也能学习稀疏数据间的二阶交互， 但说白了，这个还是个线性模型， 且交互仅仅限于二阶交互， 所以作者认为，FM在处理真实数据的时候，表达能力并不是太好。

NFM这里同样是有着组合的味道，但是人家不是那么简单的拼接式组合了，而是设计了一种结构，NFM的核心创新点是Bi-Interaction池化部分来代替其他模型使用的拼接。把FM和DNN拼接了起来。这样一来同样是利用了FM和DNN的优势。

二、NFM模型介绍

改进的思路就是用一个表达能力更强的函数来替代原FM中二阶隐向量内积的部分。

 而这个表达能力更强的函数呢， 我们很容易就可以想到神经网络来充当，因为神经网络理论上可以拟合任何复杂能力的函数， 所以作者真的就把这个f (x)换成了一个神经网络，当然不是一个简单的DNN， 而是依然底层考虑了交叉，然后高层使用的DNN网络， 这个也就是我们最终的NFM网络了：

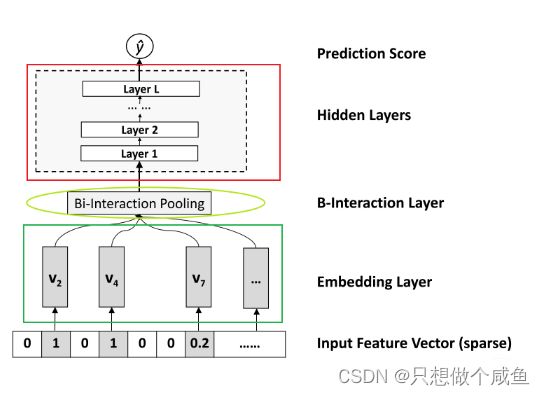
1、Input和Embedding层 

输入层的特征， 文章指定了稀疏离散特征居多， 这种特征我们也知道一般是先one-hot, 然后会通过embedding，处理成稠密低维的。 这个地方真正实现的时候，往往先LabelEncoder一下(而不是one-hot encoder)， 这样就直接能够得到那些取值非0的特征对应的embedding向量了， 毕竟LabelEncoder一下就相当于为某个特征的所有取值建立了一个字典， 我们知道在取某个值的embedding向量的时候， 直接去字典的索引值就好了(one-hot Encoder * 嵌入矩阵其实也是取得为1的那个值，就是索引值其实）

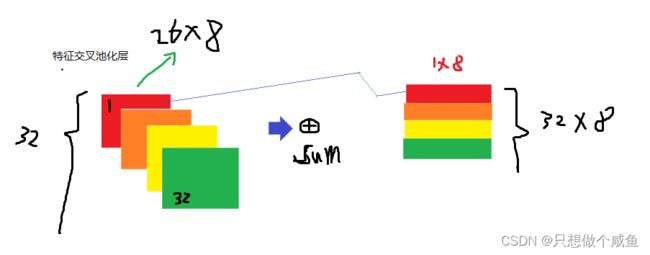
2、Bi-Interaction Pooling layer

在Embedding层和神经网络之间加入了特征交叉池化层算是本paper最大的创新点了，也正是因为这个东西，才实现了FM与DNN的无缝连接， 组成了一个大的网络，且能够正常的反向传播。假设是所有特征embedding的集合，

 ⊙表示两个向量的元素积操作，即两个向量对应维度相乘得到的元素积向量（可不是点乘呀），要注意这个地方不是两个隐向量的内积，而是元素积，这一个交叉完了之后k个维度不求和，最后会得到一个向量，

参考FM，可以将上式转化为：

在特征交叉层上，作者使用了dropout技术：为了防止过拟合

还用了BatchNormalization技术：避免embedding向量的更新将输入层的分布更改为隐藏层或输出层。

3、隐藏层

还是全连接的神经网络

 4、预测层

最后一层的结果直接过一个隐藏层，但注意由于这里是回归问题，没有加sigmoid激活：

 NFM模型的前向传播过程总结如下：

 三、pytorch代码实现

1、数据预处理

"""导入包"""
import numpy as np
import pandas as pd

from sklearn.preprocessing import MinMaxScaler, LabelEncoder
from sklearn.model_selection import train_test_split

"""特征处理"""
def sparseFeature(feat, feat_num, embed_dim=4):
    """
    create dictionary for sparse feature
    :param feat: feature_name
    :param feat_num: the total number of sparse features that do not repeat
    :param embed_dim: embedding dimension
    :return
    """
    return {'feat': feat, 'feat_num': feat_num, 'embed_dim': embed_dim}

def denseFeature(feat):
    """
    create dictionary for dense feature
    :param feat: dense feature name
    : return
    """
    return {'feat': feat}


# 读入数据集，并进行预处理
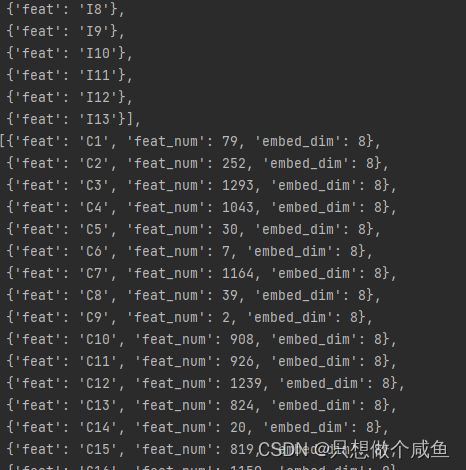
def create_cretio_data(embed_dim=8, test_size=0.2):
    # import data
    train_df = pd.read_csv('./data/train.csv')
    test_df = pd.read_csv('./data/test.csv')

    # 进行数据合并
    label = train_df['Label']
    del train_df['Label']

    data_df = pd.concat((train_df, test_df))
    del data_df['Id']

    print(data_df.columns)
    # 特征分开类别
    sparse_feas = [col for col in data_df.columns if col[0] == 'C']
    dense_feas = [col for col in data_df.columns if col[0] == 'I']

    # 填充缺失值
    data_df[sparse_feas] = data_df[sparse_feas].fillna('-1')
    data_df[dense_feas] = data_df[dense_feas].fillna(0)

    # 把特征列保存成字典, 方便类别特征的处理工作
    feature_columns = [[denseFeature(feat) for feat in dense_feas]] + [
        [sparseFeature(feat, len(data_df[feat].unique()), embed_dim=embed_dim) for feat in sparse_feas]]
    np.save('preprocessed_data/fea_col.npy', feature_columns)

    # 数据预处理
    # 进行编码  类别特征编码
    for feat in sparse_feas:
        le = LabelEncoder()
        data_df[feat] = le.fit_transform(data_df[feat])

    # 数值特征归一化
    mms = MinMaxScaler()
    data_df[dense_feas] = mms.fit_transform(data_df[dense_feas])

    # 分开测试集和训练集
    train = data_df[:train_df.shape[0]]
    test = data_df[train_df.shape[0]:]

    train['Label'] = label

    # 划分验证集
    train_set, val_set = train_test_split(train, test_size=0.2, random_state=2020)

    # 保存文件
    train_set.reset_index(drop=True, inplace=True)
    val_set.reset_index(drop=True, inplace=True)

    train_set.to_csv('preprocessed_data/train_set.csv', index=0)
    val_set.to_csv('preprocessed_data/val_set.csv', index=0)
    test.to_csv('preprocessed_data/test_set.csv', index=0)



create_cretio_data()

其中 feature_columns，结果如下：

 2、导入数据

file_path = './preprocessed_data/'


def prepared_data(file_path):
    # 读入训练集， 验证集和测试集
    train = pd.read_csv(file_path + 'train_set.csv')
    val = pd.read_csv(file_path + 'val_set.csv')
    test = pd.read_csv(file_path + 'test_set.csv')

    trn_x, trn_y = train.drop(columns='Label').values, train['Label'].values
    val_x, val_y = val.drop(columns='Label').values, val['Label'].values
    test_x = test.values

    fea_col = np.load(file_path + 'fea_col.npy', allow_pickle=True)

    return fea_col, (trn_x, trn_y), (val_x, val_y), test_x
"""导入数据"""
fea_cols, (trn_x, trn_y), (val_x, val_y), test_x = prepared_data(file_path)
# 把数据构建成数据管道
dl_train_dataset = TensorDataset(torch.tensor(trn_x).float(), torch.tensor(trn_y).float())
dl_val_dataset = TensorDataset(torch.tensor(val_x).float(), torch.tensor(val_y).float())

dl_train = DataLoader(dl_train_dataset, shuffle=True, batch_size=32)
dl_val = DataLoader(dl_val_dataset, shuffle=True, batch_size=32)

 3、模型搭建

DNN网络部分：

class Dnn(nn.Module):
    def __init__(self, hidden_units, dropout=0.):
        """
        hidden_units: 列表， 每个元素表示每一层的神经单元个数， 比如[256, 128, 64], 两层网络， 第一层神经单元128， 第二层64， 第一个维度是输入维度
        dropout = 0.
        """
        super(Dnn, self).__init__()

        self.dnn_network = nn.ModuleList(
            [nn.Linear(layer[0], layer[1]) for layer in list(zip(hidden_units[:-1], hidden_units[1:]))])
        self.dropout = nn.Dropout(dropout)

 NFM模型

class NFM(nn.Module):
    def __init__(self, feature_columns, hidden_units, dnn_dropout=0.):
        """
        NFM:
        :param feature_columns: 特征信息， 这个传入的是fea_cols
        :param hidden_units: 隐藏单元个数， 一个列表的形式， 列表的长度代表层数， 每个元素代表每一层神经元个数
        """
        super(NFM, self).__init__()
        self.dense_feature_cols, self.sparse_feature_cols = feature_columns

        # embedding
        self.embed_layers = nn.ModuleDict({
            'embed_' + str(i): nn.Embedding(num_embeddings=feat['feat_num'], embedding_dim=feat['embed_dim'])
            for i, feat in enumerate(self.sparse_feature_cols)
        })

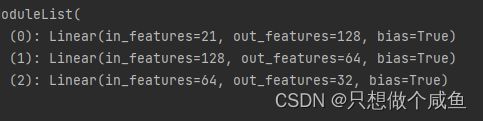
        # 这里要注意Pytorch的linear和tf的dense的不同之处， 前者的linear需要输入特征和输出特征维度， 而传入的hidden_units的第一个是第一层隐藏的神经单元个数，这里需要加个输入维度
        self.fea_num = len(self.dense_feature_cols) + self.sparse_feature_cols[0]['embed_dim']
        hidden_units.insert(0, self.fea_num)

        self.bn = nn.BatchNorm1d(self.fea_num)
        self.dnn_network = Dnn(hidden_units, dnn_dropout)
        self.nn_final_linear = nn.Linear(hidden_units[-1], 1)

    def forward(self, x):
        dense_inputs, sparse_inputs = x[:, :len(self.dense_feature_cols)], x[:, len(self.dense_feature_cols):]
        sparse_inputs = sparse_inputs.long()  # 转成long类型才能作为nn.embedding的输入
        sparse_embeds = [self.embed_layers['embed_' + str(i)](sparse_inputs[:, i]) for i in
                         range(sparse_inputs.shape[1])]
        sparse_embeds = torch.stack(sparse_embeds)  # embedding堆起来， (field_dim, None, embed_dim)
        sparse_embeds = sparse_embeds.permute((1, 0, 2))
        # 这里得到embedding向量之后 sparse_embeds(None, field_num, embed_dim), 进行特征交叉层，按照那个公式
        embed_cross = 1 / 2 * (
                torch.pow(torch.sum(sparse_embeds, dim=1), 2) - torch.sum(torch.pow(sparse_embeds, 2), dim=1)
        )  # (None, embed_dim)

        # 把离散特征和连续特征进行拼接作为FM和DNN的输入
        x = torch.cat([embed_cross, dense_inputs], dim=-1)  #32*21    8+13
        # BatchNormalization
        x = self.bn(x)
        # deep
        dnn_outputs = self.nn_final_linear(self.dnn_network(x))
        outputs = F.sigmoid(dnn_outputs)

        return outputs

其中： sparse_embeds

torch.pow(torch.sum(sparse_embeds, dim=1), 2) - torch.sum(torch.pow(sparse_embeds, 2),
如下所示:

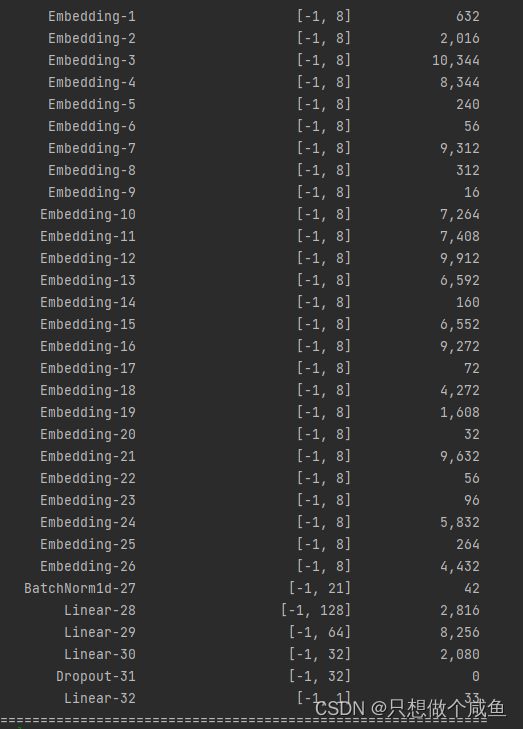
模型整体结构

 模型结果

 总结

NFM相比较于其他模型的核心创新点是特征交叉池化层，有了它，实现了FM和DNN的无缝连接，DNN可以在low level就学习到包含更多信息的组合特征。集合了FM二阶交叉线性和DNN高阶交叉非线性的优势，非常适合处理稀疏数据的场景任务
在特征交叉层和隐藏层加入dropout技术，有利于缓解过拟合，dropout也是线性隐向量模型过拟合的策略
在NFM中，使用BN+Dropout的组合会使得学习的稳定性下降， 具体使用的时候要注意
特征交叉池化层能够较好的对二阶特征信息的交互进行学习编码，这时候，就会减少DNN的很多负担，只需要很少的隐藏层就可以学习到高阶特征信息， 也就是NFM相比之前的DNN， 模型结构更浅，更简单，但是性能更好，训练和调参更容易
NFM对参数初始化相对不敏感，也就是不会过度依赖于预训练，模型的鲁棒性较强
深度学习模型的层数不总是越深越好， 太深了会产生过拟合的问题，且优化起来也会困难