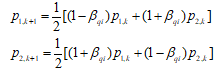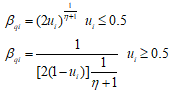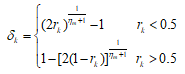NSGA-II算法介绍

博主毕设用到了，记录下来防忘记，比较具体，也分享给需要学习的同学。

1995年，Srinivas和Deb提出了非支配遗传（Non-dominated Sorting Genetic Algorithms，NSGA）算法[42]。NSGA算法是以遗传算法为基础并基于Pareto最优概念得到的。NSGA算法与基本遗传算法的主要区别是其在进行选择操作之前对个体进行了快速非支配排序，增大了优秀个体被保留的概率[43]，而选择、交叉、变异等操作与基本遗传算法无异。经过诸多学者的研究测试，NSGA算法比传统的多目标遗传算法效果更好。但是在实际应用中发现NSGA算法仍具有一定的缺点，主要体现在以下方面：

（1）算法计算量大。NSGA算法的计算复杂度与种群数量N、目标函数个数m的关系为T = O(mN3)，当种群规模较大、目标函数较多时所耗时间较长。

（2）没有应用精英策略。未通过精英策略提高优秀个体的保留概率，因而无法加快程序的执行速度。

（3）需要人为地指定共享半径σshare，对于经验的要求非常高。

为了改善NSGA算法的缺点，Deb等人在2002年提出了NSGA-II算法[44]。相对于NSGA算法，NSGA-II算法主要在以下三个方面做了改进：

（1）NSGA-II算法使用了快速非支配排序法，将算法的计算复杂度由O(mN3)降到了O(mN2)，使得算法的计算时间大大减少。

（2）采用了精英策略，将父代个体与子代个体合并后进行非支配排序，使得搜索空间变大，生成下一代父代种群时按顺序将优先级较高的个体选入，并在同级个体中采用拥挤度进行选择，保证了优秀个体能够有更大的概率被保留。

（3）用拥挤度的方法代替了需指定共享半径的适应度共享策略，并作为在同级个体中选择优秀个体的标准，保证了种群中个体的多样性，有利于个体能够在整个区间内进行选择、交叉和变异。

实践证明，NSGA-II算法无论在优化效果还是运算时间等方面都比NSGA算法有了一定的改进，是一种优秀的多目标优化算法。

1、 选择、交叉、变异

遗传算法中个体的编码方式主要有实数编码、二进制编码、格雷编码等，根据系统容量一般较大的特点，本文选择实数编码方式。在优化过程中，个体的好坏依赖于个体的适应度，适应度高的个体有更大的可能被保留进入下一代。在实际操作当中，适应度一般为个体的目标函数。

（1）选择

选择操作模仿自然界中的“优胜劣汰”法则，若个体的适应度高则其有更大概率被遗传到下一代，反之则概率较小。进行选择操作的方法有许多，比如轮盘赌选择、排序选择、最优个体保存、随机联赛选择等。

a. 轮盘赌选择：将种群中所有个体的适应度值加和，并把每个个体的适应度值与和的比值作为该个体选择的选择概率，从而个体适应度越高被选中概率越高。

b. 排序选择：按照适应度值大小对所有个体进行排序，并根据排序确定个体被选中的概率。

c. 最优个体保存：会将父代群体中的最优的个体直接保存入子代个体中，保证了优秀个体能够遗传到下一代。

d. 随机联赛选择：设置固定值k，每次随机取k个个体，将其中适应度最高的个体遗传入下一代。

这些选择方法各有优缺点，应根据不同场景、不同要求进行选择，本研究采用随机联赛选择方法。

 （2）交叉

交叉操作模拟自然界中染色体的交叉换位现象，用于生成新个体，决定了算法的全局搜索能力。标准的NSGA-II算法使用模拟二进制交叉算子，第k+1代个体的计算公式如下[44, 45]：

                                    

式中，p1,k+1和p2,k+1是交叉后生成的第k+1代个体；p1,k和p2,k是被选中的第k代个体；βqi是均匀分布因子,其计算方式如下：

式中，ui是属于[0,1)的随机数；η是交叉分布指数，一般的定义为20~30，η的大小会影响产生的个体距离父代个体的远近。

（3）变异

变异操作是模拟生物的基因变异，同交叉操作一样，都用于产生新个体。标准NSGA-II算法的变异算子为多项式变异算子，第k+1代个体的计算公式如下[44,45]:

 

式中，pk是被选中的第k代个体；pk+1是pk经变异操作得到的第k+1代个体；pmax k和pmin k分别为决策变量的上界和下界；δk计算公式如下：

 

式中，rk为[0,1]中的均匀分布随机数；ηm为变异分布指数。

2、快速非支配排序

快速非支配排序是在Pareto支配基础上提出的概念。假设有k个目标函数记为fi (x)，其中i是1, 2, … , k中的任意整数，j同样是1,2, …, k中的任意整数，但i≠j。若个体x1和x2对于任意的目标函数都有fi(x1) < fi(x2)则称个体x1支配x2；若对于任意的目标函数都有fi(x1) ≤ fi(x2)且至少有一个目标函数使得fj(x1) < fj(x2)成立则称x1弱支配x2；若既存在目标函数使得fi(x1) ≤ fi(x2)成立又存在目标函数满足fj(x1) > fj(x2)，则称个体x1和x2互不支配。

种群中的每个个体都有两个参数ni和Si，ni为种群中支配个体i 的个体数量，Si是被个体i支配的个体的集合,快速非支配排序的步骤如下：

（1）通过循环比较找到种群中所有ni = 0的个体，赋予其非支配等级为1，并将这些个体存入非支配集合rank1中。

（2）集合rank1中的每一个个体，将其所支配的个体集合中的每个个体的nj都减去1，若nj-1=0则将个体j存入集合rank2中，并赋予其中的个体非支配等级2。

（3）之后对rank2中的个体重复上述操作，直至所有个体都被赋予了非支配等级。

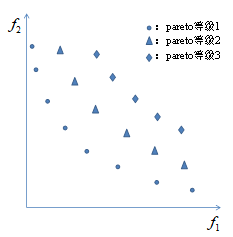
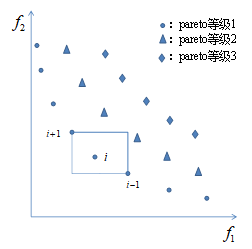
非支配等级也称作Pareto等级，其中Pareto等级为1的个体由于不受其他个体的支配，叫做非支配解，也叫 Pareto最优解，而解集所形成的曲线叫做Pareto前沿。以有两个目标函数f1和f2为例，假设经过快速非支配排序之后共分成了三个Pareto等级，如图4.1所示。图4.1中用圆圈表示的个体即Pareto等级为1的个体组成的集合为本例的Pareto最优解，这些个体形成的曲线即为本例的Pareto前沿。

 

 

 

3、拥挤度计算

在NSGA算法中，需要指定共享半径σshare，这对经验要求较高，为了克服这一缺点，NSGA-II引用了拥挤度的概念。拥挤度表示空间中个体的密度值，直观上可以用个体  周围不包括其他个体的长方形表示，如图所示。

 

在对某个等级的个体进行拥挤度计算时，设该等级共有m个个体，每个个体用xi表示，i为1~m中的任意整数，xi-1，xi+1分别为i=2, 3, …, m-1时个体  前后的个体；记第  个个体的拥挤度为yi，初始值设为0；设有n个目标函数，记为fk(x)，k=1, 2, …, n，记fmin k、fmax k分别为m个个体中目标函数值fk(xi)的最小值和最大值，拥挤度计算的伪代码流程如下所示：

for k<=n

{

    // 根据目标函数值fk(xi)对该等级的全部个体进行排序

    y1=∞

    ym=∞

    i=2

for i<m

{

i=i+1

}

k=k+1

}

4、精英策略

NSGA-II算法引入了精英策略，达到保留优秀个体淘汰劣等个体的目的。精英策略通过将父代与子代个体混合形成新的群体，扩大了产生下一代个体时的筛选范围。以图所示的例子进行分析，图中P表示父代种群，设其中的个体数量为n，Q表示子代种群，具体步骤如下：

（1）将父代种群和子代种群合并形成新的种群。之后对新种群进行非支配排序，本例中将种群分成了6个Pareto等级。

（2）进行新的父代的生成工作，先将Pareto等级为1的非支配个体放入新的父代集合当中，之后将Pareto等级为2的个体放入新的父代种群中，以此类推。

（3）若等级为k的个体全部放入新的父代集合中后，集合中个体的数量小于n，而等级为k+1的个体全部放入新的父代集合中后，集合中的个体数量大于n，则对第k+1等级的全部个体计算拥挤度并将所有个体按拥挤度进行降序排列,之后将等级大于k+1的个体全部淘汰。本例中可以看出k为2，所以对Pareto等级为3的个体计算拥挤度并按其进行降序排序，等级为4~6的个体全部淘汰。

（4） 将等级k+1中的个体按步骤2中排好的顺序逐个放入新的父代集合中，直到父代集合中的个体数量等于n，剩余的个体被淘汰。

 

 

5、算法的实现步骤

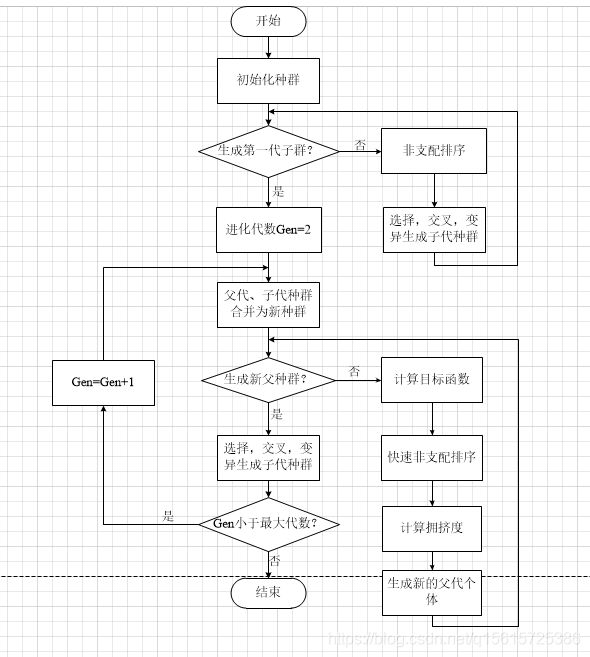
NSGA-II算法的流程图如图4.4所示，具体实现过程如下：

第一步：初始种群并设置进化代数Gen=1。

第二步：判断是否生成了第一代子种群，若已生成则令进化代数Gen=2，否则，对初始种群进行非支配排序和选择、高斯交叉、变异从而生成第一代子种群并使进化代数Gen=2。

第三步：将父代种群与子代种群合并为新种群。

第四步：判断是否已生成新的父代种群，若没有则计算新种群中个体的目标函数，并执行快速非支配排序、计算拥挤度、精英策略等操作生成新的父代种群；否则，进入第五步。

第五步：对生成的父代种群执行选择、交叉、变异操作生成子代种群。

第六步：判断Gen是否等于最大的进化代数，若没有则进化代数Gen=Gen+1并返回第三步；否则，算法运行结束。