图注意力网络——Graph attention networks (GAT)
文章目录
- 摘要
- 引言
- GAT结构
- 数据集与评估结果
- 未来改进方向
- 参考文献
摘要
图注意力网络,一种基于图结构数据的新型神经网络架构,利用隐藏的自我注意层来解决之前基于图卷积或其近似的方法的不足。通过堆叠层,节点能够参与到邻居的特征,可以(隐式地)为邻域中的不同节点指定不同的权值,而不需要任何代价高昂的矩阵操作(如反转),也不需要预先知道图的结构。通过这种方法,该模型克服了基于频谱的故神经网络的几个关键挑战,并使得模型适用于归纳和推理问题。在四个数据集上实现或匹配了最先进的结果(Cora, Citeseer, Pubmed citation network, protein-protein interaction dataset)。
引言
注意力机制的几个有趣特性:
- 操作是高效的,因为它在节点间并行处理;
- 通过给邻居确定任意的权重,它可以被用于具有不同度的图节点
- 模型直接适用于归纳学习问题,包括模型必须推广到完全看不见的图的任务
使用四个数据集对方法进行验证:Cora, Citeseer, Pubmed citation networks, protein-protein interaction。
GAT结构
本节中,作者介绍了用于构建任意图注意力网络的构建块层,并直接概述其理论和实践的优点,以及与之前在神经图处理领域的工作相比的局限性。实验使用的特定的注意力设置紧密遵循Bahdanau et al.(2015)的工作,但是该框架对于特定注意力机制的选择是不可知的。
- 层的输入:一组节点特征 h = { h ⃗ 1 , h ⃗ 2 , . . . , h ⃗ N , h ⃗ i ∈ R F } h=\{ \ \vec{h}_{1}, \vec{h}_{2}, ..., \vec{h}_{N}, \vec{h}_{i} \in \mathbb{R} ^{F} \} h={ h1,h2,...,hN,hi∈RF},其中 N N N表示节点的数量, F F F是每个节点的特征数量。
- 层的输出:一组新的节点特征(可能有着不同基数 F ′ F' F′) h ′ = { h ′ ⃗ 1 , h ′ ⃗ 2 , . . . , h ′ ⃗ N , h ′ ⃗ i ∈ R F ′ } h'=\{ \ \vec{h'}_{1}, \vec{h'}_{2}, ..., \vec{h'}_{N}, \vec{h'}_{i} \in \mathbb{R} ^{F'} \} h′={ h′1,h′2,...,h′N,h′i∈RF′}
为了获得足够的表达能力将输入特征转化为更高层次的特征,至少需要一个可学习的线性变换。因此,作为第一步,被使用一个权重矩阵参数化的一个共享线性变换 W ∈ R F ′ × F W \in \mathbb{R}^{F'\times F} W∈RF′×F被应用于每一个节点。然后对节点执行自注意力——一个共享的注意力机制,计算注意力系数。
e i j = a ( W h ⃗ i , W h ⃗ j ) (1) e_{ij}=a(W\vec{h}_{i}, W\vec{h}_{j}) \tag{1} eij=a(Whi,Whj)(1)
e i j e_{ij} eij表示节点 j j j的特征对节点 i i i的重要性。
在最一般的形式中,模型允许每个节点参与其他节点的活动,删除了所有的结构信息。通过使用掩码注意力机制将图结构注入到机制中去,对节点计算 e i j , j ∈ N i e_{ij}, j\in \mathcal{N}_{i} eij,j∈Ni, N i \mathcal{N}_{i} Ni是图中节点 i i i的邻居。在文中的实验里,它是节点 i i i(包含 i i i)的一阶邻居。为了使系数在不同的节点之间容易比较,作者使用softmax函数对所有j选项进行归一化:
α i j = s o f t m a x j ( e i j ) = e x p ( e i j ) ∑ k ∈ N i e x p ( e i k ) (2) \alpha_{ij}=softmax_{j}(e_{ij})=\frac{exp(e_{ij})}{\sum_{k\in\mathcal{N}_{i}}exp(e_{ik})} \tag{2} αij=softmaxj(eij)=∑k∈Niexp(eik)exp(eij)(2)
实验中,注意力机制 a a a是一种单层前馈神经网络,由一个权重向量 a ⃗ ∈ R 2 F ′ \vec{a} \in \mathbb{R}^{2F'} a∈R2F′参数化,并使用负斜率为0.2(即 α = 0.2 \alpha=0.2 α=0.2)的LeakyReLU非线性。完全展开后,注意力机制计算的系数可以表示为:
α i j = e x p ( L e a k y R e L U ( a ⃗ T [ W h ⃗ i ∣ ∣ W h ⃗ j ] ) ) ∑ k ∈ N i e x p ( L e a k y R e L U ( a ⃗ T [ W h ⃗ i ∣ ∣ W h ⃗ j ] ) ) (3) \alpha_{ij}=\frac{ exp(LeakyReLU(\vec{a}^{T}[W\vec{h}_{i}||W\vec{h}_{j} ])) }{ \sum_{k\in\mathcal{N}_{i}}exp( LeakyReLU(\vec{a}^{T}[W\vec{h}_{i}||W\vec{h}_{j} ]) ) } \tag{3} αij=∑k∈Niexp(LeakyReLU(aT[Whi∣∣Whj]))exp(LeakyReLU(aT[Whi∣∣Whj]))(3)
一旦得到归一化的注意力系数,那么它可以被用来计算与之对应的特征的线性组合,作为每个节点的最后输出特征。
h ′ ⃗ i = σ ( ∑ j ∈ N i α i j W h ⃗ j ) (4) \vec{h'}_{i}=\sigma(\sum_{j\in\mathcal{N}_{i}}\alpha_{ij}W\vec{h}_{j}) \tag{4} h′i=σ(j∈Ni∑αijWhj)(4)
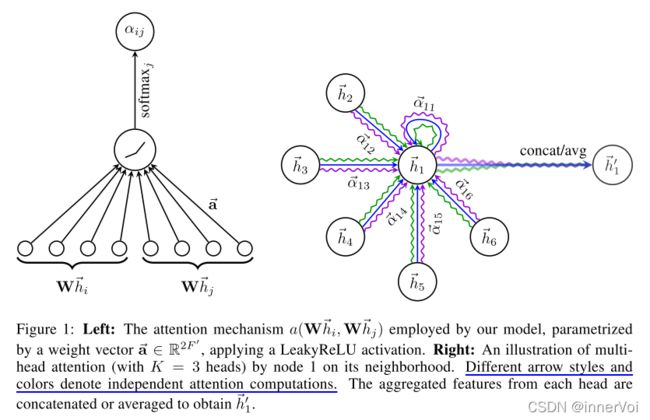
为了使自注意力的学习过程稳定,作者发现使用多头注意力对机制是有益的。使用K个独立的注意力机制执行如式(4)的转换,然后它们的特征被连接得到如下输出的特征表示。
h ′ ⃗ i = ∣ ∣ k = 1 K σ ( ∑ j ∈ N i α i j k W k h ⃗ j ) (5) \vec{h'}_{i}=||^{K}_{k=1}\sigma (\sum_{j\in\mathcal{N}_{i}}\alpha^{k}_{ij}W^{k}\vec{h}_{j}) \tag{5} h′i=∣∣k=1Kσ(j∈Ni∑αijkWkhj)(5)
其中, ∣ ∣ || ∣∣表示拼接操作, α i j k \alpha^{k}_{ij} αijk表示第k个注意力机制计算得到的归一化注意力系数, W k W^{k} Wk是相应输入线性变换的权重矩阵。
特别地,如果在网络的最后一层(预测层)上执行多头注意力,连接就不再有意义了。因此,作者使用了平均,并延迟作用于最后的非线性。
h ′ ⃗ i = σ ( 1 K ∑ k = 1 K ∑ j ∈ N i α i j k W k h ⃗ j ) (6) \vec{h'}_{i}=\sigma(\frac{1}{K}\sum_{k=1}^{K}\sum_{j\in\mathcal{N}_{i}}\alpha^{k}_{ij}W^{k}\vec{h}_{j}) \tag{6} h′i=σ(K1k=1∑Kj∈Ni∑αijkWkhj)(6)
GAT的注意力机制和多头注意力如下面论文中:
图注意层解决了先前使用神经网络对图结构数据建模方法中存在的几个问题:
- 计算高效:自注意力层的操作可以在所有边之间并行进行,同时所有节点的输出特征的计算也可以并行。不需要特征分解以及类似代价较高的矩阵操作。一个单GAT注意力头计算 F ‘ F‘ F‘特征的时间复杂度可以表示为 O ( ∣ V ∣ F F ′ + ∣ E ∣ F ′ ) O(|V|FF'+|E|F') O(∣V∣FF′+∣E∣F′)。该复杂度与如图卷积网络等的基线方法相当。应用多头注意力将使存储和参数需求增加K倍,而独立的注意力头的计算是完全独立的,可以并行化。
- 与GCNs相反,GAT模型允许(隐式地)将不同的重要性分配给同一邻居的节点,从而实现了模型容量的提升。此外,分析学习到的注意权重可能会带来可解释性方面的好处。
- 注意机制以共享的方式应用于图中的所有边,因此它不依赖于对全局图结构或其所有节点(特性)的预先访问(许多先前技术的限制)。这有几个可取的意义:
a. 图不需要是无向的(可以保留)。
b. 它使所提技术可以直接用于归纳学习——包括在训练过程中完全看不见的图上评估模型的任务。 - Hamilton等人(2017)最近发表的归纳方法对每个节点的固定大小的邻域进行采样,以保持其计算足迹的一致性;这不允许它在执行推断时访问整个邻域。此外,当使用基于LSTM (Hochreiter & Schmidhuber, 1997)的邻域聚合器时,该技术取得了一些最强大的结果。这假设邻域间存在一个一致的连续节点排序,作者通过不断地向LSTM提供随机排序的序列来纠正它。而GAT的技术不会受到这两个问题的影响,它处理整个邻域(以牺牲可变的计算空间为代价,这仍然与GCN等方法相当),并且不假设其中有任何顺序。
- GAT可以重新表述为一个MoNet(Monti et al., 2016)的特殊实例,更具体的来说,设置伪坐标函数为 u ( x , y ) = f ( x ) ∣ ∣ f ( y ) u(x,y)=f(x)||f(y) u(x,y)=f(x)∣∣f(y), f ( x ) f(x) f(x)代表节点 x x x的特征, ∣ ∣ || ∣∣代表拼接操作,并且让权重函数为 w j ( u ) = s o f t m a x ( M L P ( u ) ) w_{j}(u)=softmax(MLP(u)) wj(u)=softmax(MLP(u))(在一个节点的所有邻域上执行Softmax)会使得MoNet的patch算子与GAT相似。不过有一点需要注意,与之前考虑的MoNet实例相比,GAT模型使用节点特征进行相似性计算,而不是节点的结构属性(这将假设预先知道图结构)。
作者能够生成一个利用稀疏矩阵操作的GAT层版本,将存储复杂度降低到线性的节点和边的数量,并使GAT模型能够在更大的图数据集上执行。然而,文中使用的张量操作框架只支持对2阶张量的稀疏矩阵乘法,这限制了当前实现的层的批处理能力(特别是对于具有多个图的数据集)。合适地处理这个约束是未来工作的一个重要方向。取决于图形结构的规律性,在这些稀疏的场景中,与cpu相比,gpu可能无法提供主要的性能优势。还应该注意的是,GAT模型的“接受域”的大小是由网络的深度决定的(类似于GCN和类似的模型)。跳跃式连接(He et al., 2016)等技术可以很容易地应用于适当扩展深度。最后,跨所有边的并行化,特别是分布式的并行化,可能会涉及大量的冗余计算,因为兴趣图的邻域经常会高度重叠。
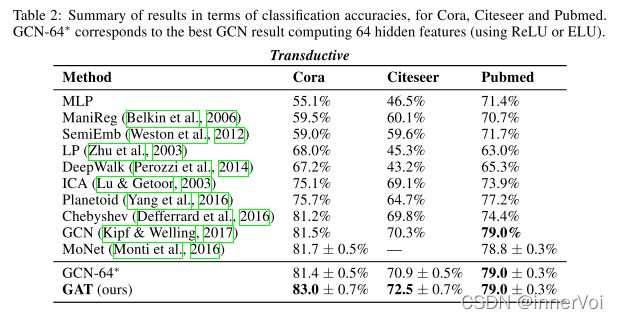
数据集与评估结果
未来改进方向
图注意力网络有几个潜在的改进和扩展,可以在未来的工作中解决,例如克服论文中2.2小节中描述的实际问题,以便能够处理更大的批处理大小。一个特别有趣的研究方向是利用注意机制对模型的可解释性进行深入分析。此外,从应用的角度来看,将该方法扩展到进行图分类而不是进行节点分类也是相关的。最后,扩展模型以合并边缘特征(指示节点之间的关系)将允许我们处理更广泛的问题。
参考文献
[1] Veličković P, Cucurull G, Casanova A, et al. Graph attention networks[J]. arXiv preprint arXiv:1710.10903, 2017.
[2] Bahdanau D, Cho K, Bengio Y. Neural machine translation by jointly learning to align and translate[J]. arXiv preprint arXiv:1409.0473, 2014.
[3] Federico Monti, Davide Boscaini, Jonathan Masci, Emanuele Rodol`a, Jan Svoboda, and Michael M Bronstein. Geometric deep learning on graphs and manifolds using mixture model cnns. arXiv preprint arXiv:1611.08402, 2016.
[4] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 770–778, 2016.