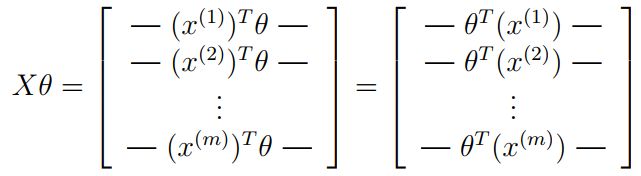吴恩达ML WEEK5 练习二（逻辑回归）+神经网络表示+练习三（多分类）

---

0 总结

学习时间：2022.10.3~2022.10.9

• 完成练习二：逻辑回归及逻辑回归的正则化代码编写
• 学习神经网络的假设函数和前向传播的表示
• 学习如何使用神经网络解决多分类问题
• 完成练习三：逻辑回归多分类部分

---

1 练习二：逻辑回归

---

1.1 逻辑回归

==背景：==假设你是一个大学系的管理员，你需要根据每个申请人的两次考试的结果决定录取机会。

1.1.1 可视化数据

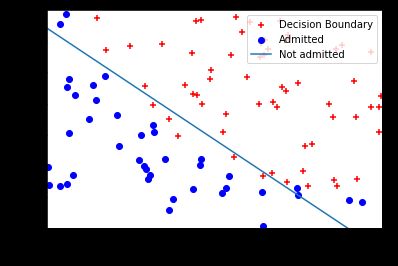
任务：完成plotData.py，画出figure1，横轴和纵轴是两个考试分数，正和负样本用不同符号表示。
代码：参考链接: python绘制散点图

def plot_data(X, y):
    plt.figure()

    # ===================== Your Code Here =====================
    # Instructions : Plot the positive and negative examples on a
    #                2D plot, using the marker="+" for the positive
    #                examples and marker="o" for the negative examples
    #
    # 分离正负样本
    positive = X[y==1]
    negative = X[y==0]

    plt.scatter(positive[:,0],positive[:,1],marker='+',c='red',label='Admitted') #画出正样本
    plt.scatter(negative[:,0],negative[:,1],marker='o',c='blue',label='Not Admitted') #画出正样本

结果

1.1.2 sigmoid函数

tips：np.r_是按列连接两个矩阵，就是把两矩阵上下相加，要求列数相等。
np.c_是按行连接两个矩阵，就是把两矩阵左右相加，要求行数相等。
sigmoid函数：
$$g(z)=\frac{1}{1+e^{-z}}$$
任务：完成sigmoid函数
代码：

def sigmoid(z):
    # 初始化
    g = np.zeros(z.size)

    # ===================== Your Code Here =====================
    # Instructions : Compute the sigmoid of each value of z (z can be a matrix,
    #                vector or scalar
    #
    # Hint : Do not import math
    g = 1/(1+np.exp(-z))

    return g

1.1.3 代价函数和梯度

tips：$$h_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}x}}$$$$J(\theta )=\frac{1}{m}\sum _{i=1}^{m}Cost(h_{\theta }(x^{(i)}),y^{(i)})$$其中：
$$Cost(h_{\theta }(x),y)=-ylog(h_{\theta }(x))-(1-y)log(1-h_{\theta }(x))$$注意：$y=0$或者$y=1$。
所以，代价函数：
$$\begin{array}{rl}J(\theta )& =\frac{1}{m}\sum _{i=1}^{m}Cost(h_{\theta }(x^{(i)}),y^{(i)})\\ & =-\frac{1}{m}[\sum _{i=1}^m{y}^{(i)}log(h_{\theta }(x^{(i)}))+(1-y^{(i)})log(1-h_{\theta }(x^{(i)}))]\end{array}$$当前要做的是：寻找合适的参数$\theta$使得$J(\theta )$最小；找到$\theta$后，在给定某个输入$x$可以预测出$h_{\theta }(x)$。
作法：
Repeat{
$$\begin{array}{rl}{\theta }_j& :={\theta }_j-\alpha \frac{\partial J(\theta )}{\partial {\theta }_j}\\ & :={\theta }_j-\alpha \sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}\end{array}$$}
任务：完成costFunction.py
注意：如果dot的两个参数是向量，则只要求他们的维度相等就可以直接dot。
代码：

def cost_function(theta, X, y):
    m = y.size

    # You need to return the following values correctly
    cost = 0
    # n+1
    grad = np.zeros(theta.shape)

    # ===================== Your Code Here =====================
    # Instructions : Compute the cost of a particular choice of theta
    #                You should set cost and grad correctly.
    #
    # 计算cost和grad
    # 假设函数h是m维向量
    h = sigmoid(np.dot(X,theta))
    # 
    term1 = -np.dot(y,np.log(h))
    term2 = -np.dot(1-y,np.log(1-h))
    cost = (term1 + term2)/m
    grad = np.dot(h-y,X)/m


    # ===========================================================

    return cost, grad

运行结果：

1.1.3 fmin_bfgs优化函数

代码：

'''
    fmin_bfgs优化函数 
    第一个参数是计算代价的函数 
    第二个参数是计算梯度的函数 
    参数x0传入初始化的theta值
    maxiter设置最大迭代优化次数
'''
theta, cost, *unused = opt.fmin_bfgs(f=cost_func, fprime=grad_func, x0=initial_theta, maxiter=400, full_output=True, disp=False)

运行结果：

1.1.4 评估逻辑回归

任务：完成predict.py，输入48和45，会得到录取概率为0.776。
代码：

def predict(theta, X):
    m = X.shape[0]

    # Return the following variable correctly
    p = np.zeros(m)

    # ===================== Your Code Here =====================
    # Instructions : Complete the following code to make predictions using
    #                your learned logistic regression parameters.
    #                You should set p to a 1D-array of 0's and 1's
    #
    p = sigmoid(X.dot(theta))
    p[p>=0.5] = 1
    p[p<0.5] = 0

    # ===========================================================

    return p

---

1.2 正则化的逻辑回归

1.2.1 数据可视化

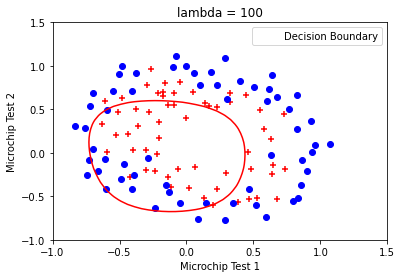
数据没有被直线分割成正和负两部分，因此线性的逻辑回归并不能很好地分割这部分数据集。

1.2.2 特征映射（！重要）

一个更好地拟合数据的方法是创造更多的特征。在mapFeauture.py中，我们将两个特征映射成x1、x2的六次方的特征多项式。

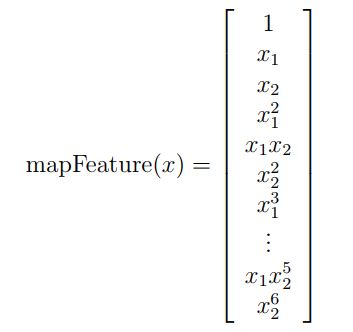
这样我们就将两个特征变成28位的向量。在这组高纬度的特征向量训练出来的逻辑回归分类器，将有更复杂的决策边界和非线性。但是，也可能会出现过拟合问题，因此我们需要对逻辑回归进行正则化。

1.2.3 代价函数的梯度

任务：完成costFunctionReg.py
注意：python下标从0开始，如图所示：

代码：

def cost_function_reg(theta, X, y, lmd):
    m = y.size

    # You need to return the following values correctly
    cost = 0
    grad = np.zeros(theta.shape)

    # ===================== Your Code Here =====================
    # Instructions : Compute the cost of a particular choice of theta
    #                You should set cost and grad correctly.
    #
    # h:(m,1)
    h = sigmoid(X.dot(theta))
    m1 = -y.dot(np.log(h))
    m2 = -(1-y).dot(np.log(1-h))
    m3 = theta[1:].dot(theta[1:])
    cost = (m1+m2)/m + lmd*m3/(2*m)

    grad = X.T.dot(h-y)/m 
    grad[1:] += theta[1:]*lmd/m

    # ===========================================================

    return cost, grad

运行结果：

1.2.4 决策边界

任务：使用fmin_bfgs训练参数$\theta$，并绘制决策边界。使用不同的KaTeX parse error: Undefined control sequence: \ambda at position 1: \̲a̲m̲b̲d̲a̲，观察决策边界的变化。
结果：

---

2 神经网络的表示

---

2.1 神经网络假设函数

逻辑单元

输入为$x_0,x_1,x_2,x_3$，$x_0$为偏差单元，有时候不写，永远为1。
激励函数为sigmoid函数。
假设函数为$h_{\theta }(x)=\frac{1}{1+e^{-z}}$
权重为$\theta$

神经网络

Layer1：输入层，Layer2：隐藏层（可不止一层），Layer3：输出层。
$a_i^j$：第$j$层的第$i$个激活项。（上角标表示层数）
${\Theta }^j$：第$j$层到第$j+1$层的权重。
如果神经网络在第$j$层有$s_j$个单元，在第$j+1$层有$s_{j+1}$个单元，那么${\Theta }_j=s_{j+1}\times (s_j+1)$（不包含1），比如这里，${\Theta }_1\in {\mathbb{R}}^{3\times 4}$

---

2.2 前向传播

如图，假设输入:$$x=a^{(1)}=\left[\begin{array}{c}{x}_0\\ x_1\\ x_2\\ x_3\end{array}\right]\in {\mathbb{R}}^4$$，其中$x_0=1$。那么，定义：$$z^{(2)}=\left[\begin{array}{c}{z}_1^{(2)}\\ z_2^{(2)}\\ z_3^{(2)}\end{array}\right]=\left[\begin{array}{c}{\Theta }_{10}^{(1)}{x}_0+{\Theta }_{11}^{(1)}{x}_1+{\Theta }_{12}^{(1)}{x}_2+{\Theta }_{13}^{(1)}{x}_3\\ {\Theta }_{20}^{(1)}{x}_0+{\Theta }_{21}^{(1)}{x}_1+{\Theta }_{22}^{(1)}{x}_2+{\Theta }_{23}^{(1)}{x}_3\\ {\Theta }_{30}^{(1)}{x}_0+{\Theta }_{31}^{(1)}{x}_1+{\Theta }_{32}^{(1)}{x}_2+{\Theta }_{33}^{(1)}{x}_3\end{array}\right]={\Theta }^{(1)}{a}^{(1)}\in {\mathbb{R}}^3$$,理解到矩阵中每一行是该层某个神经元的计算公式。那么：$$a^{(2)}=g(z^{(2)})\in {\mathbb{R}}^3$$，其中，$g$为sigmoid函数。至此，第二层三个神经元的值计算出来了。
将$a_0^{(2)}=1$加入到矩阵$a^{(2)}$中，$a^{(2)}$变为四维向量。
重复上述步骤：$$z^{(3)}={\Theta }^{(2)}{a}^{(2)},$$$$h_{\Theta }(x)=a^{(3)}=g(z^{(3)})$$。

---

2.3 神经网络应用举例

逻辑与

可以看到，当$\Theta =\left[\begin{array}{c}-30\\ 20\\ 20\end{array}\right]$的时候，这个神经网络可以模拟逻辑与。
逻辑或

可以看到，当$\Theta =\left[\begin{array}{c}-10\\ 20\\ 20\end{array}\right]$的时候，这个神经网络可以模拟逻辑或。

---

2.4 同或门

利用之前设计的神经网络设计一个同或门。
（！看清楚颜色对应）

---

2.5 多分类问题

---

3 练习三：多分类问题和神经网络

---

3.1 多分类问题

data = scio.loadmat('ex3data1.mat')
X = data['X']
y = data['y'].flatten()

ex3data1.mat中数据：
一共有5000个样本，每个样本是20x20像素的图像。每个像素使用浮点数表示灰度。y是1-10的数字。现在需要使用逻辑回归和神经网络识别手写数字0~9。

3.1.1 数据可视化

随机抽取的100个样本示例。

3.1.2 逻辑回归向量化

代价函数
在没有正则化的逻辑回归中，代价函数的表达式：

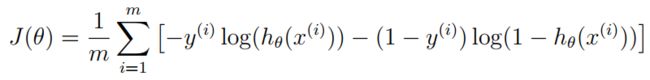
因此我们需要先计算$h_{\theta }(x^{(i)})$，假设函数表达式如下：

因此我们定义：

$m$：样本个数。
$x^{(i)}$：第$i$个样本的n+1个数据，是列向量。

则有：

如果$a$和$b$是向量，则$a^{T}b$=$b^{T}a$

梯度
在没有正则化的逻辑回归中，梯度的表达式：

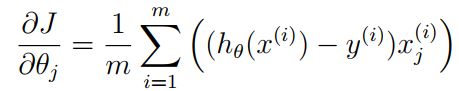
将每一步的偏导写出：

任务：完成lrCostFunctio.py
代码：（正则化）

def compute_cost(theta,X,y,lmd):
    cost = 0
    m = y.size
    h = sigmoid(X.dot(theta))

    temp1 = -np.dot(y.T,np.log(h))
    temp2 = -np.dot((1-y).T,np.log(1-h))
    temp3 = np.dot(theta[1:].T,theta[1:])
    cost = (temp1+temp2)/m+temp3*lmd/(2*m)

    return cost

def compute_grad(theta,X,y,lmd):
    m = y.size
    grad = np.zeros(theta.shape)

    h = sigmoid(X.dot(theta))
    temp4 = h-y
    grad = np.dot(X.T, temp4)/m
    grad[1:] += theta[1:]*lmd/m

    return grad

def lr_cost_function(theta, X, y, lmd):
    
    cost = compute_cost(theta, X, y, lmd)
    grad = compute_grad(theta, X, y, lmd)

    return cost, grad

运行结果：

3.1.3 多分类问题

在多分类问题中，参数矩阵$\Theta \in {\mathbb{R}}^{K\times (N+1)}$，K为分类的类别个数，也就是说，每一行表示了每一类的参数。在手写识别问题中，$K=10$，注意到$y=10$的时候，表示手写图片是0。
任务：完成oneVsAll.py
代码：

def one_vs_all(X, y, num_labels, lmd):
    # Some useful variables
    (m, n) = X.shape

    # You need to return the following variables correctly
    all_theta = np.zeros((num_labels, n + 1))
    initial_theta = np.zeros(n+1)

    # Add ones to the X data 2D-array
    X = np.c_[np.ones(m), X]

    # 循环：每一类进行一次循环
    # i = 0,1,2,...num_labels-1
    for i in range(num_labels):
        print('Optimizing for handwritten number {}...'.format(i))
        # ===================== Your Code Here =====================
        # Instructions : You should complete the following code to train num_labels
        #                logistic regression classifiers with regularization
        #                parameter lambda
        #
        #
        # Hint: you can use y == c to obtain a vector of True(1)'s and False(0)'s that tell you
        #       whether the ground truth is true/false for this class
        #
        # Note: For this assignment, we recommend using opt.fmin_cg to optimize the cost
        #       function. It is okay to use a for-loop (for c in range(num_labels) to
        #       loop over the different classes
        #
        
        
        # 手写数字0的时候y=10
        iclass = i if i  else 10
        y_temp = np.array([1 if iy == iclass else 0 for iy in y ])
        ''' fmin_cg优化函数 第一个参数是计算代价的函数 第二个参数是计算梯度的函数 参数x0传入初始化的theta值
            args传入训练样本的输入特征矩阵X,对应的2分类新标签y,正则化惩罚项系数lmd
            maxiter设置最大迭代优化次数
        '''
        res = opt.fmin_cg(lCF.compute_cost,fprime = lCF.compute_grad,x0 = initial_theta,\
                                    args=(X,y_temp,lmd),maxiter=50,disp=False,full_output=True)
        all_theta[i] = res[0]
        # ============================================================    
        print('Done')

    return all_theta

3.1.4 多分类预测

任务：完成predictOneVsAll.py
tips: argmax的用法
代码：

def predict_one_vs_all(all_theta, X):
    m = X.shape[0]
    num_labels = all_theta.shape[0]

    # You need to return the following variable correctly;
    p = np.zeros(m)

    # Add ones to the X data matrix
    X = np.c_[np.ones(m), X]

    # ===================== Your Code Here =====================
    # Instructions : Complete the following code to make predictions using
    #                your learned logistic regression parameters (one vs all).
    #                You should set p to a vector of predictions (from 1 to
    #                num_labels)
    #
    # Hint : This code can be done all vectorized using the max function
    #        In particular, the max function can also return the index of the
    #        max element, for more information see 'np.argmax' function.
    #

    poss = sigmoid(X.dot(all_theta.T))
    # 每一行最大值的下标
    index_max = np.argmax(poss,axis = 1)
    p = np.array([index if index else 10 for index in index_max])

    return p

运行结果：