Coarse-to-Fine Region Selection and Matching

Coarse-to-Fine Region Selection and Matching

0 Abstract

提出一种宽基线匹配方法（wide baseline matching），使用图像域的层次分解和由粗到细的区域选择来匹配。

本实验通过对显著区域进行采样来降低两幅图像中所有区域的比较成本，系统去除区域以提高效率。

优点：不局限于协变显著区域，在大视角下限制大，导致对应区域很少。

通过对仿射空间进行粗到细的搜索，有效地实现了层次中区域的仿射不变匹配。

在两个基准数据集上的实验表明，在大视角变化的情况下，本实验方法比其他宽基线方法找到了更准确的对应关系(虚报率更低)。

1 Contribution

1、使用图像域的层次分解和粗到细的区域选择宽基线匹配。

2、在视点变化的情况下，分层方法比现有的基于检测器的方法找到了更正确的图像对应(更少的错误匹配)。

3、利用仿射空间的思想，展示如何通过对仿射空间的分层分解来实现区域的高效仿射不变匹配。

2 Coarse-to-Fine Matching Algorithm

本算法在两幅图像$I_1$和$I_2$之间找到对应的区域。它由两个层次结构组成，支持从粗到细的搜索。 区域分层，将图像域分解为区域。仿射层次，分解仿射空间。 接下来的两个小节将描述层次结构和从粗到细的搜索。

2.1 Coarse-to-Fine Region Selection

区域层次结构的关键属性是：

1、在层次结构的顶部的区域由大区域组成，在层次结构下方是子区域。——该属性考虑了匹配的效率：任何找到对应的区域都必然意味着所有子区域也都找到对应。因此，不需要匹配次区域。

2、任何由视点变化产生的变换都可以用层次中区域的维度变换任意地很好地逼近。——该属性是必要的，这样才能很好地逼近变换。 它还允许为匹配计算不变区域描述符，提高了效率。

使用一个区域层次结构，该区域包含通过将$I_1$ 依次分割成四个相等的矩形而形成的区域。每个区域是层次结构中的一个节点，四个相等的子矩形是该节点的子节点。

见图1：区域选择算法：通过搜索$I_2$ 中的所有邻域和位置，并通过平均归一化互相关(NCC)将这些邻域与区域进行比较，来实现从层次结构顶部的区域开始，假设区域在仿射群下变换，将每个区域与图像$I_2$ 进行匹配。

常利用NCC实现仿射对比度变化的不变性，这个过程将符合最高保真度区域的$A_1$和$A_2$的第一和第二最佳仿射变换返回到I2中的区域。

---

假设$s_1\ge s_2$，计算$I_1$ 的最佳仿射变换区域与$I_2$ 对应区域之间的NCC得分$s_1$和$s_2$。

1、第一个阈值测试：当最高分$s_1$满足$0<T1\le 1$

2、第二个阈值测试：次好与最好的分数$\frac{s2}{s1}<T2(0<T2\le 1)$，

满足1和2，该区域被接受为匹配，不访问层次结构中的子区域。

如果没有以足够的保真度通过第一个阈值测试的区域，则该区域中任何没有通过$A_1$ (该区域的变换)的第一个阈值测试的子区域都被匹配(见图2)，其他的子区域都被接受。

（Interest point method：兴趣点方法在匹配前先剔除$I_1$ 区域，只选择显著区域，减少区域比较。

本方法，regions are eliminated online：如果层次结构中的某个区域已经匹配，则不再需要再匹配子区域，减少了区域之间的比较。$I_1$中的一个区域与$I_2$中的所有区域相匹配比协变检测器限制更少，因此本方法，更多图像能够相匹配。

2.2 Coarse-to-Fine Affine Search

$R$是图像领域的子集，$I_1|R$是$I_1$限制R

（见图3）将$I_1|R$匹配到$I_2$中相应的仿射变换区域$I_2|A(R)$，这要求$I_2$ 中的每个位置都与$GL(2)$群对$I_1|r$的所有变换进行比较，其中$GL(2)$是非奇异2 × 2矩阵的一般线性群。 直接搜索所有$GL(2)$的代价很高，所以我们引入了一个层次结构来高效地搜索$GL(2)$。

假设$GL(2)$的一个有限采样。用$GL(2)$的二维子集的参数$p,q$表示，$g_p,q$表示$GL(2)$的元素$p,q$.

设$N\ge 1,P=\left\{p_1,p_2，\dots ，p_{2^N}\right\}$和$Q=\left\{q_1,q_2，\dots ，q_{2^N}\right\}$为参数p, q的集合。

层次结构如下所示，设$L$表示层次结构中的层数。在层次的第1级，$P$和$Q$被分成$2^{N-L+l}$个大小为$2^{L-l}$的子集。设$P_i^l,Q_j^l$表示这些子集，其中$i,j\in \left\{1，\dots ,2^{N-L+l}\right\}$。每个子集在$l+1$级定义的是一组在$l$级的一个子集，即$P_i^{l+1}\subset P_{\lfloor (i-1)/2\rfloor +1}^l$和$Q_j^{l+1}\subset Q_{\lfloor (j-1)/2\rfloor +1}^l$，$\lfloor \cdot \rfloor$表示the floor function。见图4。

考虑到层次结构中的一个节点在$l-1$级，表示$P_i^l,Q_j^l$(四)的集合的子集节点级别$l$。

构造一种方法来选择包含$GL(2)$参数的子集，将$I_1|R$ 转换为$I_2$中的一个匹配区域。

为了获得层次结构的速度优势，不需要将每个子集的每个单独元素下的$I_1|R$ 与$I_2$匹配。

为此，将$\left\{P_i^l,Q_j^l\right\}$中每个子集的$B_{ij}^l$定义为$I_1|R$的仿射变换的平均值，其中，仿射变换是$P_i^l,Q_j^l$中$2^{n_l}(n_l\le L-l)$样本产生的群元素。设$I_1|R◦g^{-1}$表示定义在$g(R)$上的仿射变换区域。那么$B_{ij}^l:{\cap }_{p\in P,q\in Q},g_{p,q}(R)\to R^{+}$和$B_{ij}^l=\frac{1}{2^{2n_l}}{\sum }_{p\in P,q\in Q}{I}_1|R◦g_{p,q}^{-1}$

其中$P\subset P_i^l$and$Q\subset Q_j^l$包含$2^{n_l}$个元素。其思想是，对于某些$p,q\in P_i^l,Q_j^l$，当$I_1|R◦g_{p,q}^{-1}$与$I_2$匹配时，$B_{ij}^l$应该与$I_2$ 中的匹配区域相关联。

(注意，仅使用$2^{n_l}$ 样本来提高计算速度。理想情况下，应该将所有样本平均，但实验性能表明，这是不必要的。)

设$I_2$ 中每个像素$x$的响应$R_{ij}^l(x)$表示 $B_{ij}^l$和像素x中心的$I_2$区域之间的NCC。定义$i^{\prime }{j}^{\prime }$为$\left\{P_i^l,Q_j^l\right\}$子集的指数，其包含响应的最高价值,和$x_{ij}^{\prime }$像素最高的反应。

$i\prime j\prime =\underset{ij}{\mathrm{argmax}}{R}_{ij}^l\left(x{\prime }_{ij}\right),x{\prime }_{ij}=\underset{x}{\mathrm{argmax}}{R}_{ij}^l\left(x\right)$

子集$P^l_i, Q^l_j $ 的$ij\ne i^{\prime }{j}^{\prime }$被消除，这将搜索参数的范围缩小到$P_{i^{\prime }}^l，Q_{j^{\prime }}^l$，并重复这个过程。这就是算法1。

2.3 Cost Savings of the Affine Hierarchy

研究了在仿射空间中从粗到细搜索的成本节约和方法的准确性之间的权衡。

仿射层次结构好处：可将线性搜索简化为对数搜索。 层次结构中的级别越多，计算量就越少。

但层次结构中级别越多，意味着层次结构顶部的区域对更广泛程度的转换具有鲁棒性，但差别较小，这可能会导致错误的匹配。

---

在转盘数据集上进行实验研究：

参数$s\in [0.8,1.2]，\theta \in [-60^{\circ }，60^{\circ }]，h\in [-0.2,0.2]，\lambda \in [0.8,1.2]$

样本大小512和2048。

运行整个算法(包括通过区域层次结构的搜索)，并将其与使用仿射空间的直接线性搜索的区域搜索进行比较。

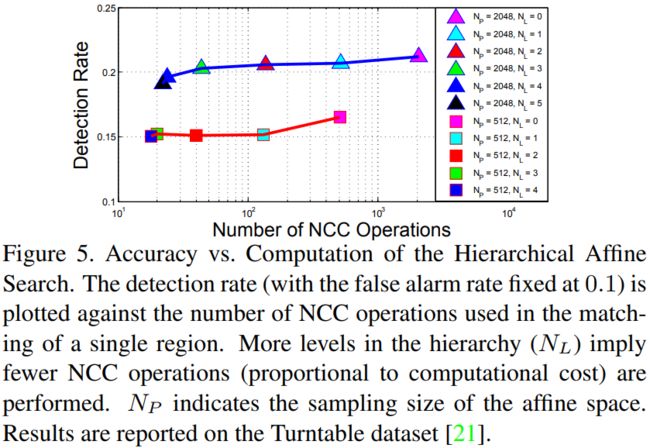
在0.1的虚警率下，选择阈值T1和T2作为最大的检测率(准确性)。

（见图5）绘制了检测率与仿射层次结构中的水平数量之间的关系，这与每个区域的响应或NCC计算数量成正比。

结果表明，牺牲0.01 ~ 0.02的检出率，每个区域可节省近200倍的NCC操作。

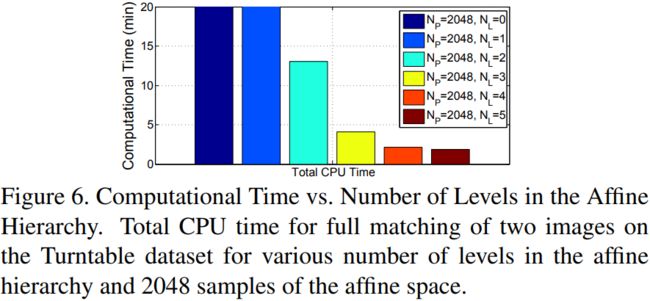
（见图6）使用MatLab代码匹配整个图像的单个处理器上的CPU运行时使用5个层次结构，比使用2048个参数的直接线性搜索，整个算法的计算时间减少了10倍。 图片为800 × 600。

3 Theoretical Justification

本节概述了使用分层图像分解的理论理由，以及本实验的仿射匹配方案的不变性性质。

3.1 Justification of the Region Hierarchy（区域等级的正当性）

从视点变化在图像面上引起的变换是分段微分同胚映射(diffeomorphism):

Definition 1

Ω上的分段微分胚φ为

1、对域${\left\{R_i\right\}}_{i=1}^n$(映射集)和O闭塞集$(R_i,O\subset \Omega )$进行分区，结果${\cup }_{i=1}^n{R}_i\cup O=\Omega$， $R_i\cap R_j=\varnothing (i\ne j)$， $R_i\cap O=\varnothing$，其中n≥1为区域个数。

2、映射${\phi }_i:R_i\to {\phi }_i(R_i)\subset \Omega$，使${\phi }_i$是一个微分同胚映射

3、$\phi :\Omega \setminus O\to \Omega$是一对一的

将φ的集合表示为$PDiff(\Omega )$

尽管与视点下两个图像相关的变换是分段微分同胚映射，但在图像的局部区域内，变换更简单:

Theorem 1

假设$\phi \in PDiff(\Omega )$和$\epsilon >0$，则存在$\left\{P_i\right\}$， $\left\{Ri\right\}$和仿射变换$A_i\in A(2)$的子划分，使得φ在每个集合$P_i$的$C^1$范数中逼近误差ε，即

$||\phi -A_i|{|}_{C^1}=\underset{x\in P_i}{\sup }|\phi (x)-A_i(x)|+|D\phi (x)-D{A}_i(x)|<\epsilon$

其中D表示雅可比矩阵。

poof：假定每个$R_i$是紧致的。由于$\phi |R_i$是一个异胚，$R_i$内部的每一点都有一个仿射变换和一个邻域，使$||\phi -A_i|{|}_{C^1}=\underset{x\in P_i}{\sup }|\phi (x)-A_i(x)|+|D\phi (x)-D{A}_i(x)|<\epsilon$满足泰勒定理。

$R_i$的边界上的每个点在$R_i$内部都有一个邻域和一个仿射变换，使得$||\phi -A_i|{|}_{C^1}=\underset{x\in P_i}{\sup }|\phi (x)-A_i(x)|+|D\phi (x)-D{A}_i(x)|<\epsilon$可以用Whitney扩展定理来满足。通过紧性，这些邻域对$R_i$存在一个有限覆盖。每个$R_i$的这些邻域构成一个满足$||\phi -A_i|{|}_{C^1}=\underset{x\in P_i}{\sup }|\phi (x)-A_i(x)|+|D\phi (x)-D{A}_i(x)|<\epsilon$的有限集$\left\{Pi\right\}$。

分割$\left\{P_i\right\}$可以用$\left\{P_i^{\prime }\right\}$区域任意地很好地逼近，这些区域由Ω依次分割成四个相等的矩形组成。这就证明了我们选择区域等级制度的合理性。通过将图像域依次分割为四部分而得到的区域上定义的有限的仿射变换集合，可以任意地很好地逼近任何分段微分同胚映射。

现有的兴趣点匹配方案利用局部亲和来设计描述子和检测器，检测器检测到的区域的仿射变换不足以近似分段微分同胚映射。

3.2 Invariants and the Affine Search

展示了本实验的仿射搜索是如何与不变描述符相关的。

设$I$表示图像集(即，对于所有子集$\Omega$，函数形式为$i:\Omega \subset R^2\to R$)。描述符是一个函数$f:I\to F$，其中F是描述集。

我们感兴趣的描述符是不变的妨害图像形成。在某些情况下，干扰可能形成一组(例如，定义域的平移、旋转和仿射变换)。描述群的某些不变量是可以完成的。用$G$表示一个组，用$g$表示$G$的一个元素。$g$对图像$i$的作用为$i◦g$。我们将描述符的不变性形式化为一个组:

Definition 2（组的不变性）设$G$为一组。描述符$f:I\to F$对G是不变的，如果对于所有$i\in I$和$g\in G,F(I◦g)=F(I)$。

---

常数函数是不变描述符，但在匹配时并不有用。极大不变量更有用:

Definition 3 (群的极大不变量)。对于组$G$不变的描述符$f:I\to F$是最大不变的，如果对于所有的$i_0,i_1\in I,F(i_0)=F(i_1)$等价于$g\in G$满足$I_0◦g=I_1$。

---

极大不变量是重要的描述符，因为它们只消除了$G$的影响。此外，所有其他不变量都是极大不变量的函数。极大不变量与轨道有关，定义为:

Definition 4 s(轨道)。设$G$是一个群，$i\in I$是一个图像。$i$的轨道表示为$[i]$，$[i]=\left\{i◦g:g\in G\right\}$。$I$中所有轨道的集合为轨道空间，用$I/G$表示，即$I/G=\left\{[i]:i\in I\right\}$。

---

极大不变量的特征为:

Theorem 2 设$G$为一组。定义一个描述符$f$为$f:I\to I/G$和$F(i)=[i]$。那么$f$是关于$G$的最大不变量。

证明，$[i]$对于$G$是不变的：让$g^{\prime }\in G$，然后$[i◦g^{\prime }]=\left\{(i◦g)◦g^{\prime }:g\in G\right\}=\left\{i◦g^{\prime \prime }:g^{\prime \prime }=g{g}^{\prime }，g\in G\right\}=\left\{i◦g^{\prime \prime }：g”\in G\right\}=[i]$，其中倒数第二个等式由一组同构元素相乘获得（where the second to last equality is obtained since multiplication by a group element is an isomorphism.）。同样，如果$[I_1]=[I_2]$，那么对于每个$g_1\in G$，存在$g_2\in G$，使得$I_1◦g_1=I_2◦g_2$。将$g_1$设置为恒等元素，则存在$g_2$，使$I_1=I_2◦g_2$，因此轨道是一个最大不变量。

要确定$[I_1]$是否= $[I_2]$，只要验证$I_2\in [I_1]$ 即可。在本仿射搜索算法中，这个性质被用来检验轨道的相等性。事实上，将一个$R^{\prime }$区域的$[i_1|R]$与$[i_2|R^{\prime }]$匹配是通过通过NCC测试轨道$[i_1|R]$与$i_2|R^{\prime }$匹配来完成的。

将$i_1|R◦g_{p,q}$除以P，Q在(1)中的子集的平均值，与不变性和轨道联系起来。

如上所述，轨道的任何函数也是一个不变量，尽管不一定是最大不变量。显然，在轨道上的积分${\int }_G{i}_1|R◦gdg$，$dg$是$Haar$测度是轨道的函数，因此是不变的。由于轨道上的平均值可能不够有区别，本算法在$G$的有限的$G^{\prime }$子集上取平均值。这使得所得到的描述子对$G^{\prime }$的小扰动具有鲁棒性。这使得描述符与$I_2$ 中相应的区域匹配，前提是$I_1|R◦g\approx I_2|R^{\prime }$，其中$ g∈G '$

4 Conclusion

引入了一种新的宽基线匹配方法来处理大视点变化。

兴趣点方法是最适合宽基线的方法，但在大视点下性能有限。 兴趣点方法使比较图像间所有区域的任务成为可能，其通过基于显著性的采样区域建立对应关系。 这在匹配之前消除了区域，但从根本上限制了性能，因为协变显著区域在图像中是稀疏的。

本实验在匹配过程中使用层次结构的区域和从粗到细的搜索系统地消除区域，增加了找到的正确对应的数量，同时减少了以不同方式比较各个区域的任务。其通过在仿射空间上使用另一个层次搜索来实现仿射不变匹配的层次区域。

是最适合宽基线的方法，但在大视点下性能有限。 兴趣点方法使比较图像间所有区域的任务成为可能，其通过基于显著性的采样区域建立对应关系。 这在匹配之前消除了区域，但从根本上限制了性能，因为协变显著区域在图像中是稀疏的。

本实验在匹配过程中使用层次结构的区域和从粗到细的搜索系统地消除区域，增加了找到的正确对应的数量，同时减少了以不同方式比较各个区域的任务。其通过在仿射空间上使用另一个层次搜索来实现仿射不变匹配的层次区域。

本方法在两个基准数据集上的大视点变化上优于现有的兴趣点方法，与比较图像之间的所有区域相比，获得了合理的计算时间和相当大的速度。