机器学习：10.机器学习---支持向量机

第1关：线性可分支持向量机

1、按照支持向量机的思想，下图哪条决策边界的泛化性最好？

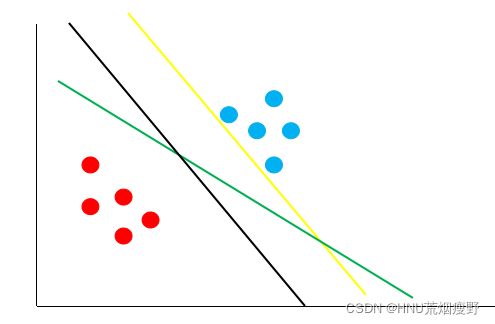
A、绿线
B、黑线
C、黄线

B

2、假设支持向量分别为
3x1+4x2+5=+1
3x1+4x2+5=−1
​如下图：

则最大间隔r的值为？
A、0.3
B、0.4
C、0.5
D、2

B

3、假设有两个样本点：(V,+1),(-V,-1)。其中，V=(3,2)，则使得间隔最大的决策边界为：
(ps:x为横坐标轴，y为纵坐标轴)
A、x=0
B、y=0
C、3x+2y=0
D、2x+3y=0

C

4、有三个样本点：(x,+1),(y,+1),(z,-1)，超平面为:a+b=1。
其中,x=(3,0),y=(0,4),z=(0,0),则以下说法错误的为：
A、超平面能够将三个样本点按类别分隔开来
B、样本y到超平面的距离为3
C、样本z到超平面的距离的平方为0.5
D、离超平面距离最近的样本为z

B

5、

图中，最大间隔决策边界为：
A、x+y+1=0
B、x-y+1=0
C、-x-y+1=0
D、-x+y+1=0

D

6、下面说法正确的是？
A、支持向量机的最终模型仅仅与支持向量有关。
B、支持向量机的最终模型由所有的训练样本共同决定。
C、支持向量机的最终模型由离决策边界最近的几个点决定。
D、训练集越大，支持向量机的模型就一定越准确。

A C

第2关：线性支持向量机

#encoding=utf8
from sklearn.svm import LinearSVC

def linearsvc_predict(train_data,train_label,test_data):
    '''
    input:train_data(ndarray):训练数据
          train_label(ndarray):训练标签
    output:predict(ndarray):测试集预测标签
    '''
    #********* Begin *********# 
    clf = LinearSVC(dual=False)
    clf.fit(train_data,train_label)
    predict = clf.predict(test_data)
    #********* End *********# 
    return predict

第3关：非线性支持向量机

#encoding=utf8
from sklearn.svm import SVC

def svc_predict(train_data,train_label,test_data,kernel):
    '''
    input:train_data(ndarray):训练数据
          train_label(ndarray):训练标签
          kernel(str):使用核函数类型:
              'linear':线性核函数
              'poly':多项式核函数
              'rbf':径像核函数/高斯核
    output:predict(ndarray):测试集预测标签
    '''
    #********* Begin *********# 
    clf =SVC(kernel=kernel)
    clf.fit(train_data,train_label)
    predict = clf.predict(test_data)
    #********* End *********# 
    return predict

第4关：序列最小优化算法

#encoding=utf8
import numpy as np
class smo:
    def __init__(self, max_iter=100, kernel='linear'):
        '''
        input:max_iter(int):最大训练轮数
              kernel(str):核函数，等于'linear'表示线性，等于'poly'表示多项式
        '''
        self.max_iter = max_iter
        self._kernel = kernel
    #初始化模型
    def init_args(self, features, labels):
        self.m, self.n = features.shape
        self.X = features
        self.Y = labels
        self.b = 0.0
        # 将Ei保存在一个列表里
        self.alpha = np.ones(self.m)
        self.E = [self._E(i) for i in range(self.m)]
        # 错误惩罚参数
        self.C = 1.0
    #********* Begin *********#    
    #kkt条件    
    def _KKT(self, i):
        y_g = self._g(i)*self.Y[i]
        if self.alpha[i] == 0:
            return y_g >= 1
        elif 0 < self.alpha[i] < self.C:
            return y_g == 1
        else:
            return y_g <= 1
    # g(x)预测值，输入xi（X[i]）
    def _g(self, i):
        r = self.b
        for j in range(self.m):
            r += self.alpha[j]*self.Y[j]*self.kernel(self.X[i], self.X[j])
        return r
    # 核函数,多项式添加二次项即可
    def kernel(self, x1, x2):
        if self._kernel == 'linear':
            return sum([x1[k]*x2[k] for k in range(self.n)])
        elif self._kernel == 'poly':
            return (sum([x1[k]*x2[k] for k in range(self.n)]) + 1)**2    
        return 0
    # E（x）为g(x)对输入x的预测值和y的差
    def _E(self, i):
        return self._g(i) - self.Y[i]
    #初始alpha
    def _init_alpha(self):
        # 外层循环首先遍历所有满足0
        index_list = [i for i in range(self.m) if 0 < self.alpha[i] < self.C]
        # 否则遍历整个训练集
        non_satisfy_list = [i for i in range(self.m) if i not in index_list]
        index_list.extend(non_satisfy_list)
        for i in index_list:
            if self._KKT(i):
                continue
            E1 = self.E[i]
            # 如果E2是+，选择最小的；如果E2是负的，选择最大的
            if E1 >= 0:
                j = min(range(self.m), key=lambda x: self.E[x])
            else:
                j = max(range(self.m), key=lambda x: self.E[x])
            return i, j
    #选择alpha参数   
    def _compare(self, _alpha, L, H):
        if _alpha > H:
            return H
        elif _alpha < L:
            return L
        else:
            return _alpha
    #训练
    def fit(self, features, labels):
        '''
        input:features(ndarray):特征
              label(ndarray):标签
        '''
        self.init_args(features, labels)
        for t in range(self.max_iter):
            i1, i2 = self._init_alpha()
            # 边界
            if self.Y[i1] == self.Y[i2]:
                L = max(0, self.alpha[i1]+self.alpha[i2]-self.C)
                H = min(self.C, self.alpha[i1]+self.alpha[i2])
            else:
                L = max(0, self.alpha[i2]-self.alpha[i1])
                H = min(self.C, self.C+self.alpha[i2]-self.alpha[i1])
            E1 = self.E[i1]
            E2 = self.E[i2]
            # eta=K11+K22-2K12
            eta = self.kernel(self.X[i1], self.X[i1]) + self.kernel(self.X[i2], self.X[i2]) - 2*self.kernel(self.X[i1], self.X[i2])
            if eta <= 0:
                continue
            alpha2_new_unc = self.alpha[i2] + self.Y[i2] * (E2 - E1) / eta
            alpha2_new = self._compare(alpha2_new_unc, L, H)
            alpha1_new = self.alpha[i1] + self.Y[i1] * self.Y[i2] * (self.alpha[i2] - alpha2_new)
            b1_new = -E1 - self.Y[i1] * self.kernel(self.X[i1], self.X[i1]) * (alpha1_new-self.alpha[i1]) - self.Y[i2] * self.kernel(self.X[i2], self.X[i1]) * (alpha2_new-self.alpha[i2])+ self.b 
            b2_new = -E2 - self.Y[i1] * self.kernel(self.X[i1], self.X[i2]) * (alpha1_new-self.alpha[i1]) - self.Y[i2] * self.kernel(self.X[i2], self.X[i2]) * (alpha2_new-self.alpha[i2])+ self.b 
            if 0 < alpha1_new < self.C:
                b_new = b1_new
            elif 0 < alpha2_new < self.C:
                b_new = b2_new
            else:
                # 选择中点
                b_new = (b1_new + b2_new) / 2
            # 更新参数
            self.alpha[i1] = alpha1_new
            self.alpha[i2] = alpha2_new
            self.b = b_new
            self.E[i1] = self._E(i1)
            self.E[i2] = self._E(i2)       
    def predict(self, data):
        '''
        input:data(ndarray):单个样本
        output:预测为正样本返回+1，负样本返回-1
        '''
        r = self.b
        for i in range(self.m):
            r += self.alpha[i] * self.Y[i] * self.kernel(data, self.X[i])
        return 1 if r > 0 else -1
    #********* End *********# 

第5关：支持向量回归

#encoding=utf8
from sklearn.svm import SVR

def svr_predict(train_data,train_label,test_data):
    '''
    input:train_data(ndarray):训练数据
          train_label(ndarray):训练标签
    output:predict(ndarray):测试集预测标签
    '''
    #********* Begin *********#
    svr = SVR(kernel='rbf',C=100,gamma= 0.001,epsilon=0.1)
    svr.fit(train_data,train_label)
    predict = svr.predict(test_data)
    #********* End *********#
    return predict