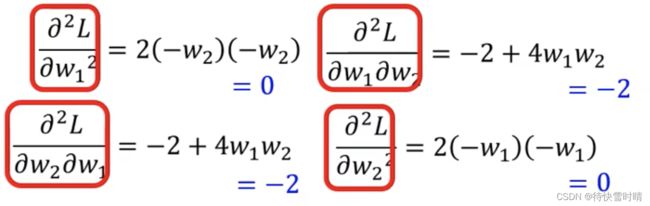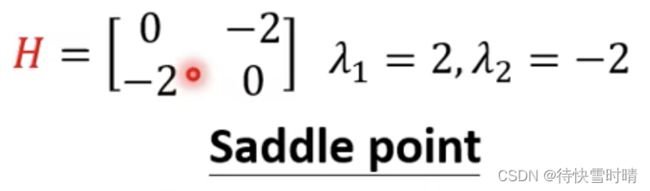【机器学习】李宏毅 - 03 神经网络优化
文章目录
- 学习总结
- Critical Point
-
- 局部最小值(local minima)
- 鞍点(saddle point)
- 判断标准
-
- 概念
- 在Critical Point附近时,需考察 H H H的特征值
-
- 实例1
- 卡在鞍点时, g g g为0,可以利用 H H H的特征向量确定参数更新方向
-
- 实例2
- 局部最小值(Local Minima)比鞍点(Saddle Point)少得多
- 批次(Batch)与动量(Momentun)
-
- Review:Optimization with Batch (Task2 05)
- Small Batch v.s. Large Batch
-
- 基本现象
- 时间性能
-
- 现象
- 原因
- 对总时间的影响
- 结论
- 动量(Momentum)
-
- Gradient Descent + Momentum
- 自动调整学习速率(Adaptive Learning Rate)
-
- 1. Training stuck ≠ Small Gradient
- 2. 应用固定的学习率时,即使是关于凸函数的 Error Surface 优化问题都很困难
-
- 基本原则
- 考虑学习率的变化,更改梯度下降公式
- 最常用的策略:Adam=RMSProp + Momentum
- Learning Rate Scheduling
-
- Learning Rate Decay
- Warm up
- 总结
- 批次标准化(Batch Normalization)简介
-
- Changing Landscape
- 结论
-
- 解决方法:Feature Normalization
- 深度学习中的应用
-
- 具体计算步骤
- 批次标准化(Batch Normalization)
-
- 引入 γ , β \gamma,\beta γ,β还原归一化后的数据
- Testing(inference)时没有Batch进行标准化/归一化 → \rightarrow → 训练时会找到 μ ˉ , σ ˉ \bar{\mu},\bar{\sigma} μˉ,σˉ
- 分类问题的损失函数
-
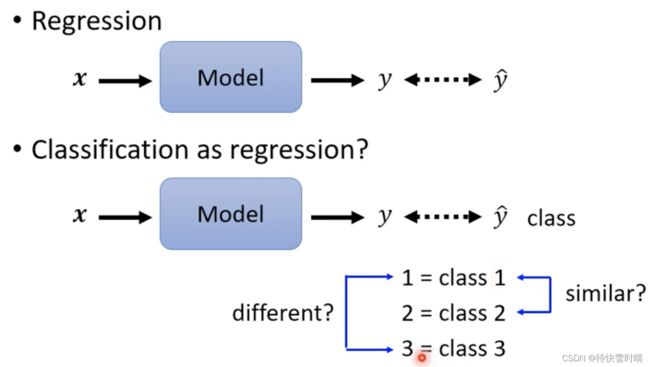
- 把分类(Classification)当作回归(Regression)来看
- Class as one-hot vector
- Classification with softmax
-
- Soft-max内部运作模式
- 分类的损失函数
-
- 优化目标
- 计算方法
- 举例
- 结论
学习总结
神经网络训练优化思维导图
Critical Point
定义:梯度(Gradient)为0的点。
Loss没有办法再下降,可能卡在了Critical Point:局部最小值(local minima)或鞍点(saddle point)。
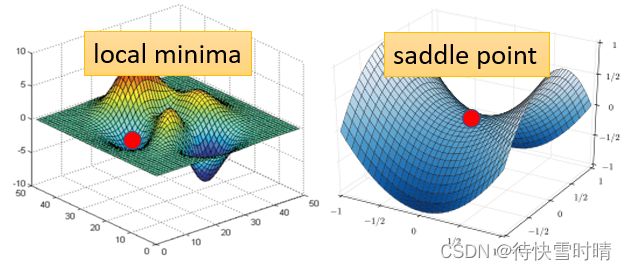
局部最小值(local minima)
卡在局部最小,则没有路可以走了。
鞍点(saddle point)
卡在鞍点,则旁边还是有路可以走。
判断标准
考察 θ \theta θ附近损失函数的梯度 → \rightarrow → 泰勒展开 → \rightarrow → 海塞矩阵 H H H
概念
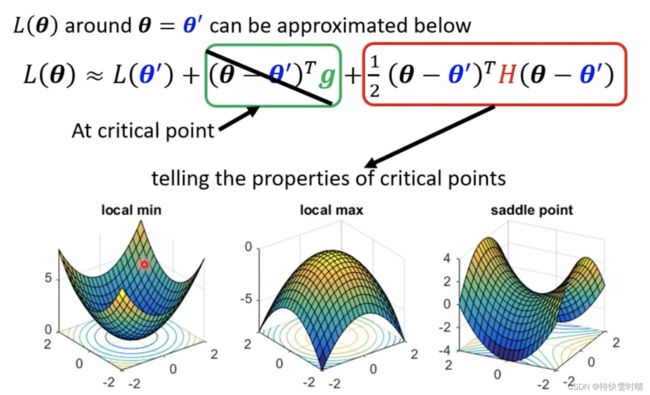
第一项中,当 θ \theta θ和 θ ′ \theta^{'} θ′很接近的时候, L ( θ ′ ) L(\theta^{'}) L(θ′)和 L ( θ ) L(\theta) L(θ)很接近。
第二项中, g g g是一个向量,代表梯度(一阶导数),可以弥补 L ( θ ′ ) L(\theta^{'}) L(θ′)和 L ( θ ) L(\theta) L(θ)之间的差距; g g g的第 i i i个component,就是 θ \theta θ的第 i i i个component对 L L L的微分。
第三项中, H H H表示海塞矩阵,是 L L L的二次微分/二阶导。
在Critical Point附近时,需考察 H H H的特征值
第二项为0,需要根据第三项来判断,考察 H H H的特征值。
- 当所有的eigen value都是正的, H H H是正定矩阵(positive definite),此时是局部最小值。
- 当所有eigen value都是负的, H H H是negative definite,此时是局部最小值。
- 当eigen value有正有负,那就是鞍点。
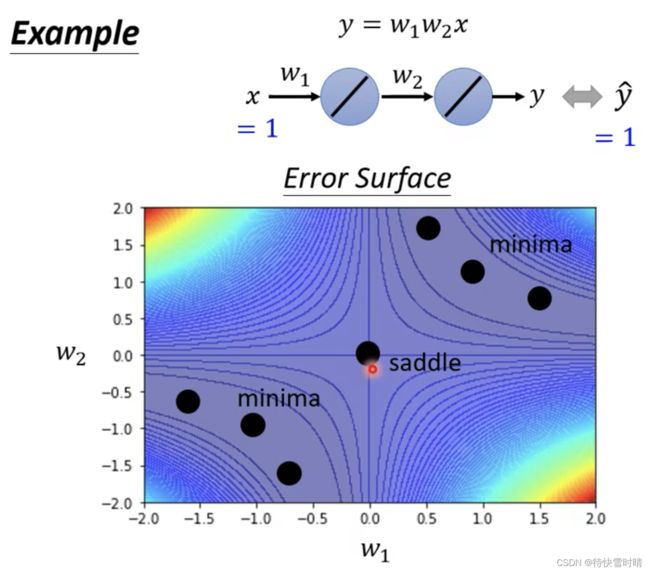
实例1
方法一:倒搜所有参数,得到所有loss的值,画出的Error Surface。
方法二:直接计算出一个点是局部最小还是鞍点。
- 观察 H H H的特征值正负
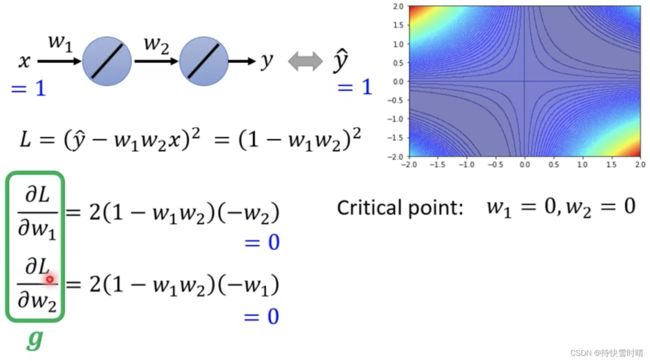
卡在鞍点时, g g g为0,可以利用 H H H的特征向量确定参数更新方向
步骤:
- 找出负的特征值(eigen value)。
- 找出对应的特征向量(eigen vector) u u u。
- 把特征向量 u u u加上 θ ′ \theta^{'} θ′,即沿着 u u u的方向更新,就可以找到一个新的点 θ \theta θ,这个点的loss比原来还要低。
实例2
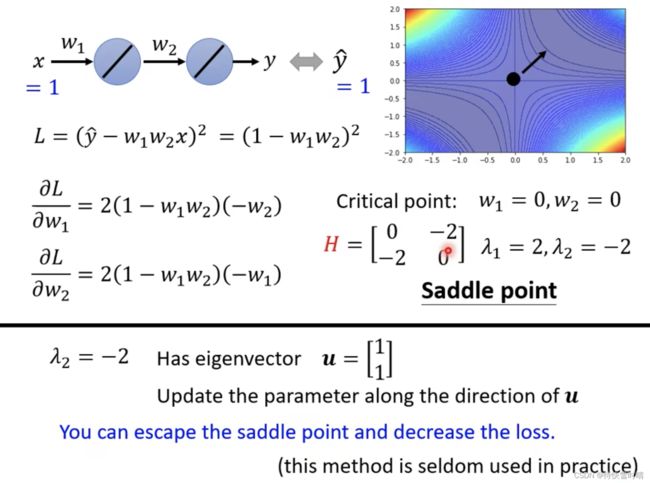
注意:该方法需要算Hessian矩阵,计算量大,实际操作中很少用到。
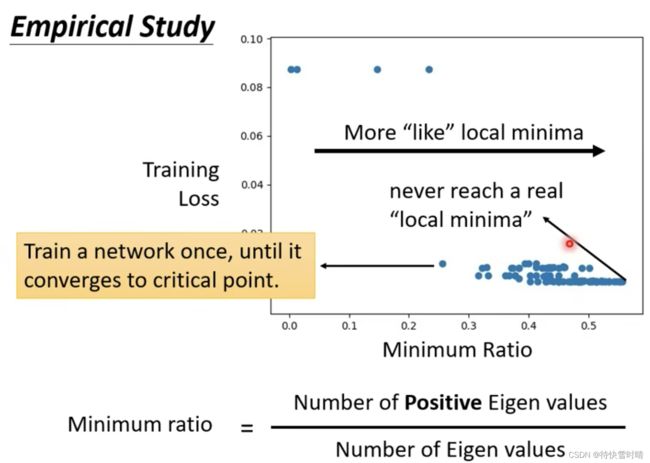
局部最小值(Local Minima)比鞍点(Saddle Point)少得多
Loss在一个高维空间中,往往只会遇到鞍点,几乎不会遇到局部最小值点 → \rightarrow → 从上图中可见,正特征值的数目最多只占所有特征值的60%,说明剩余40%的维度都仍然“有路可走”,可以让loss下降。
批次(Batch)与动量(Momentun)
总结:Small Batch size and momentum can help escape critical points.
Review:Optimization with Batch (Task2 05)
- 在更新参数时,我们拿 大B项样本数据 ,计算Loss和Gradient。
- 所有的Batch看过一遍,叫做一个Epoch。
- Shuffle:每个Epoch开始前会重新分一次batch,每一个Epoch的batch都不一样。
Small Batch v.s. Large Batch
基本现象
-
左边的情况中,必须把20个样本数据遍历一遍后,我们的参数才能更新一次。
蓄力时间长(是这样吗?学下去!),但是威力比较大
-
右边的情况中,只需要一个样本数据就能更新一次参数。显而易见,用一个样本计算出的loss,是比较有噪声( Noisy )的,所以更新的方向是曲曲折折的。
技能冷却时间短(是这样吗?学下去!),但威力不准
时间性能
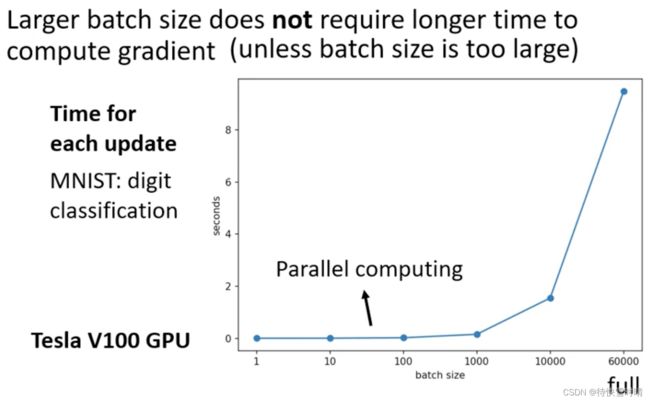
考虑并行计算(Parallel computing)时,Large Batch花费的时间不一定比较长。除非batch size过于庞大。
现象
- Batch Size从1到1000所需时间几乎一致。
- 增加到10000,乃至60000时,一个Batch所需时间随着Batch Size的增加而增长。
原因
- GPU可以做并行运算,所以1000个样本数据所需时间,并不是一个样本的1000倍。
- GPU平行运算能力有极限,当Batch Size真的非常巨大时,GPU跑完一个Batch计算出Gradient所需时间,还是会随Batch Size的增加而增长。
对总时间的影响
因为有平行运算的能力,所以当 Batch Size 小 的时候, 跑完一个Epoch花的时间比大的Batch Size还要多 ;反之, 大的Batch Size情况下,跑完一个Epoch花的时间反而少 。
那么Large Batch威力大,有了并行计算的加持后,运行时间又少,是不是百利无一害呢?
答案不然。我们看以下两张图,可以发现在Large Batch的情况下,预测精确度会随着Batch Size增大而降低。
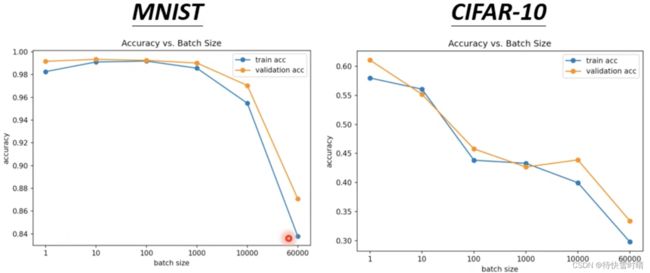
- Smaller batch size has better performance.
- “Noisy” update is better for traning.
- What’s wrong with large batch size? Optimization issue.
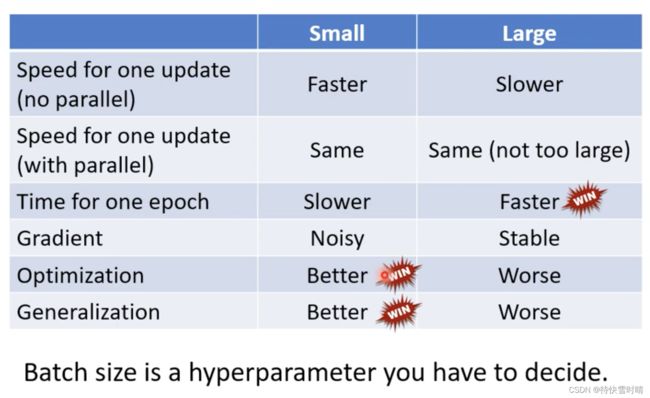
结论
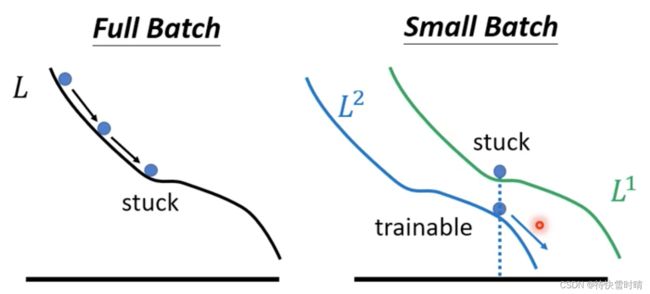
结论1: 使用较小的Batch Size,在更新参数时会有Noisy → \rightarrow → 有利于训练
使用Small Batch时,不同的Batch求得的Loss略有差异,当L1落入局部最小值卡住时,L2可以继续训练。
结论2:使用较小的Batch Size,可以避免Overfitting → \rightarrow → 有利于测试(Testing)
[On Large-Batch Training For Deep Learning,Generalization Gap And Sharp Minima] (https://arxiv.org/abs/1609.04836) 这篇 Paper 的实验结果
Training的时候都很好,Testing的时候,大的Batch对应的Testing结果差 ,代表 Overfitting 。
一种解释(尚待研究)
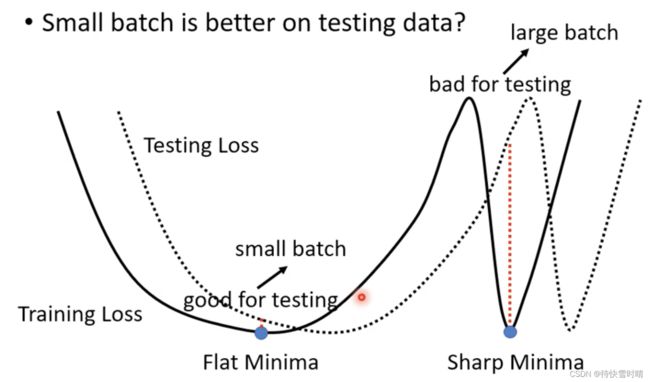
一个“峡谷里”的Local Minima是坏的极小值,而“平原上的”Local Minima是好的极小值。
把Training的Loss往右平移,对于一个在 平原上的minima 来说,它在Training和Testing上面的结果不会 差太多 ;对于在 峡谷里的minima 来说, 差别甚远 。
Large Batch会倾向于走入峡谷极小值,而Small Batch会倾向于走入平原极小值。
Large Batch顺着规定的方向更新参数,很有可能走入比较小的峡谷里。而Small Batch有多个Loss Function,每次更新方向不一样,如果峡谷很窄,可能会跳出这个峡谷最小值。
案例:综合考虑Large Batch的“高速”优势,和“较差”的优化结果。(鱼与熊掌)
动量(Momentum)
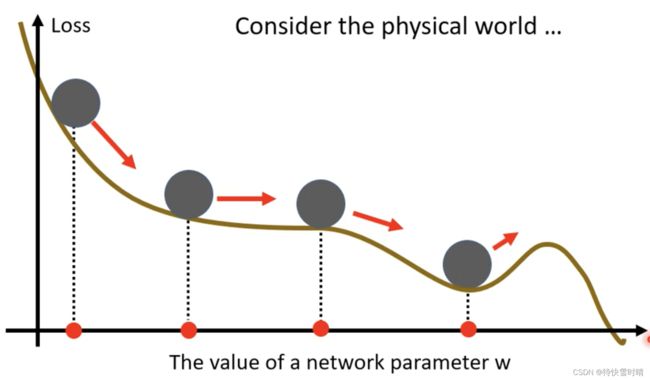
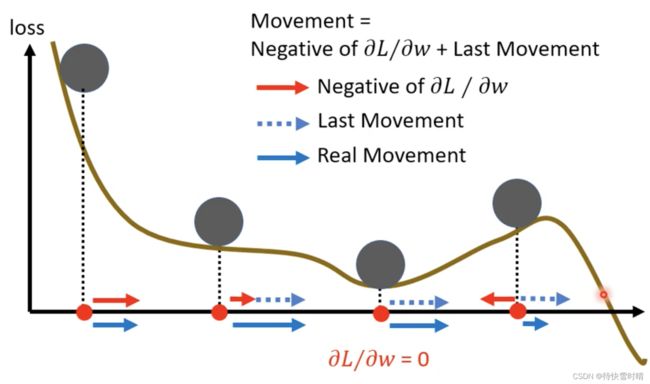
物理世界的动量,小球会有惯性越过critical point。
Vanilla Gradient Descent(一般的梯度下降):只考虑梯度的方向,向反方向移动。
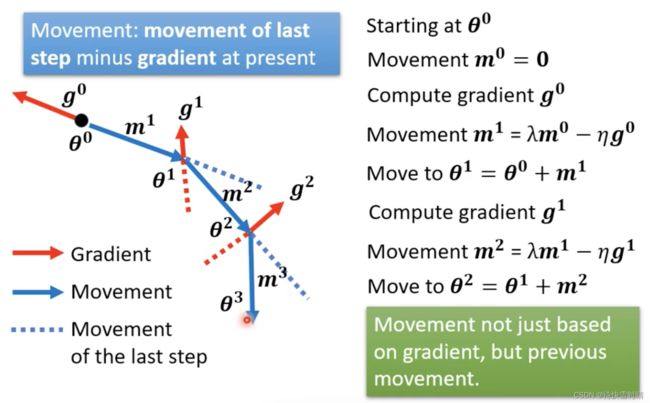
Gradient Descent + Momentum
理解:Momentum是一种改进梯度下降方向的策略,防止落入局部最小值。
不是只看gradient的方向,而是会结合之前移动的方向来调整参数,相当于考虑之前所有梯度的总和。
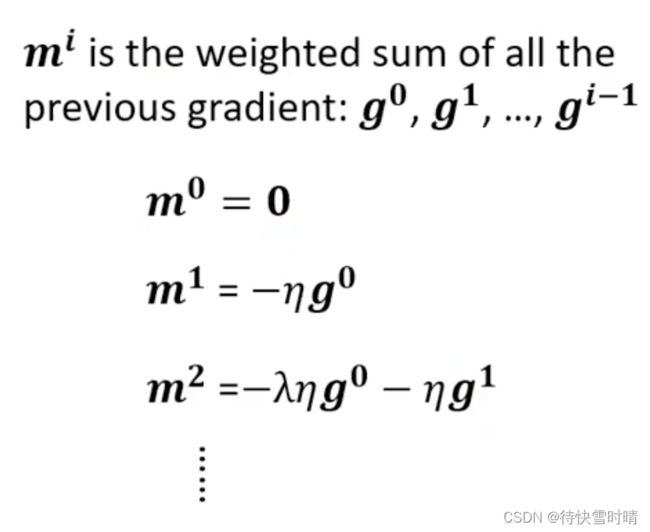
自动调整学习速率(Adaptive Learning Rate)
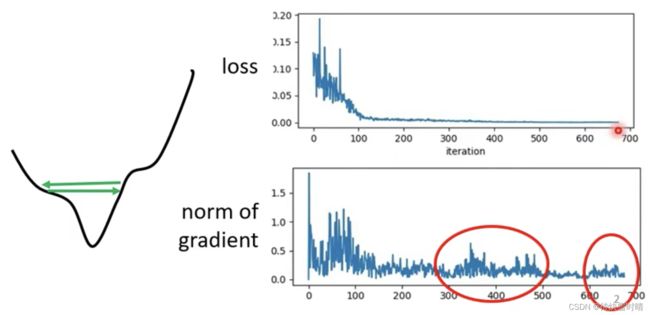
1. Training stuck ≠ Small Gradient
当Loss不再下降时,不一定到达了Critical Point(梯度等于零),梯度可能仍然很大。
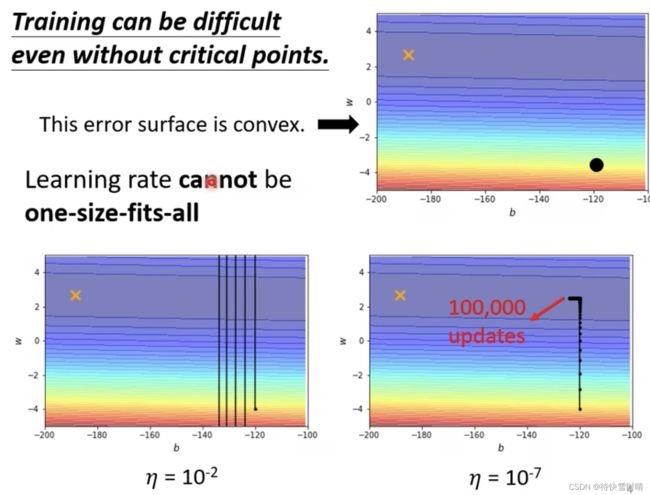
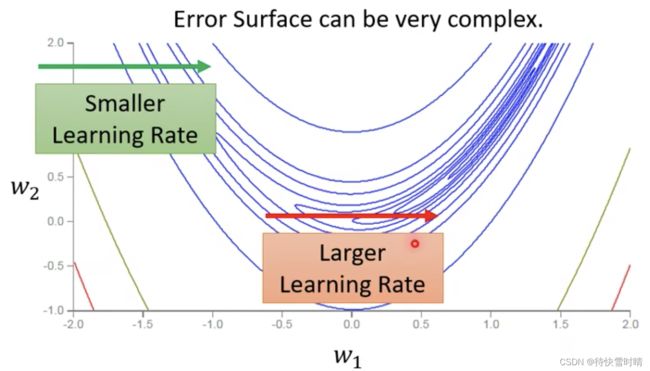
2. 应用固定的学习率时,即使是关于凸函数的 Error Surface 优化问题都很困难
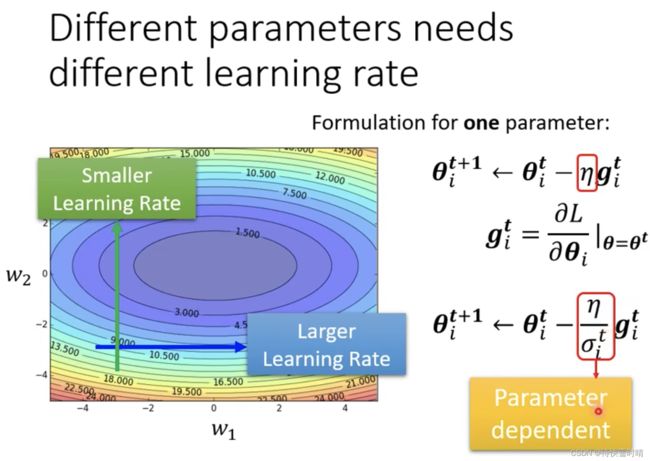
基本原则
- 某一个方向上梯度很小,非常平坦 → \rightarrow → 调大学习率
- 某一个方向上非常陡峭,坡度很大 → \rightarrow → 调小学习率
考虑学习率的变化,更改梯度下降公式
根据参数的实际情况,调整 σ i t \sigma_i^t σit的大小,实现对参数 θ i t + 1 \theta_i^{t+1} θit+1的更新。
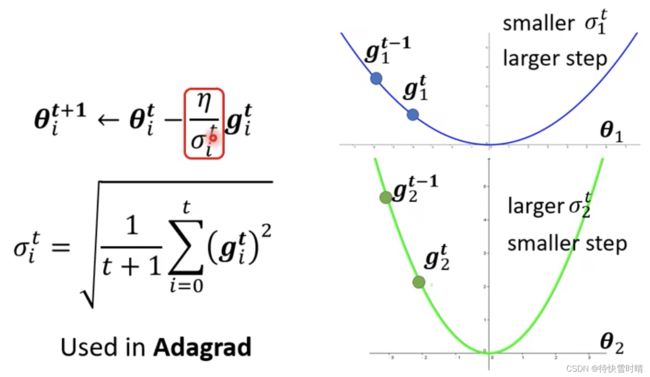
计算 σ i t \sigma_i^t σit的方式 :计算从第一步到目前为止,所有梯度的均方根(Root Mean Square)。
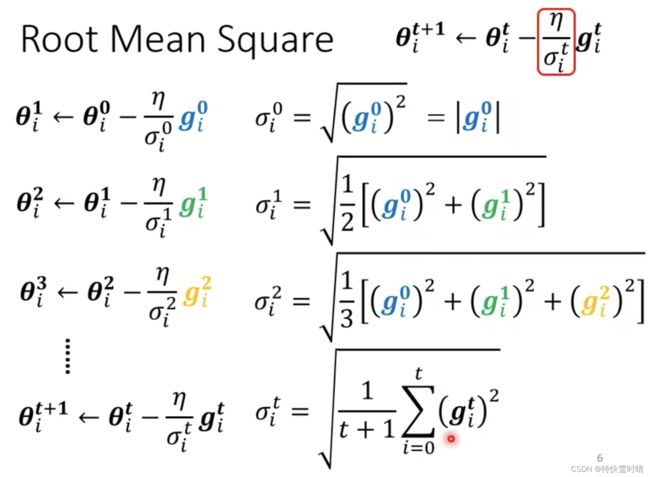
这个方法应用于 Adagrad 中。
所以我们希望学习率可以动态调整,使用 RMSProp 方法。
RMSProp
添加参数 α \alpha α,越大说明过去的梯度信息 越重要 。
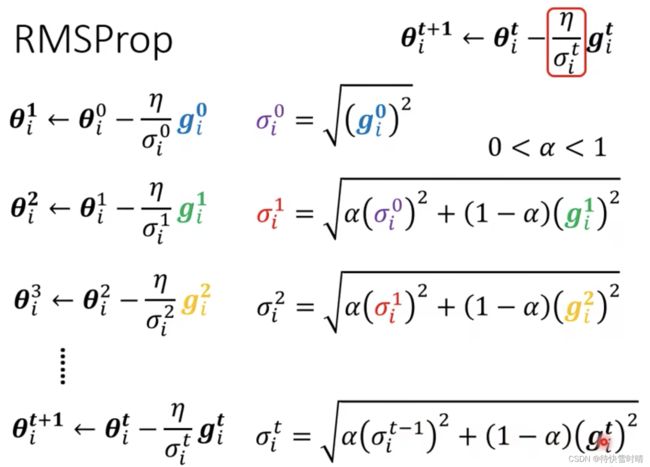
α \alpha α设很小,趋近于0时,就代表这一步算出的梯度相较于之前算出的梯度而言更重要。
α \alpha α设很大,趋近于1时,就代表这一步算出的梯度没有之前的重要。
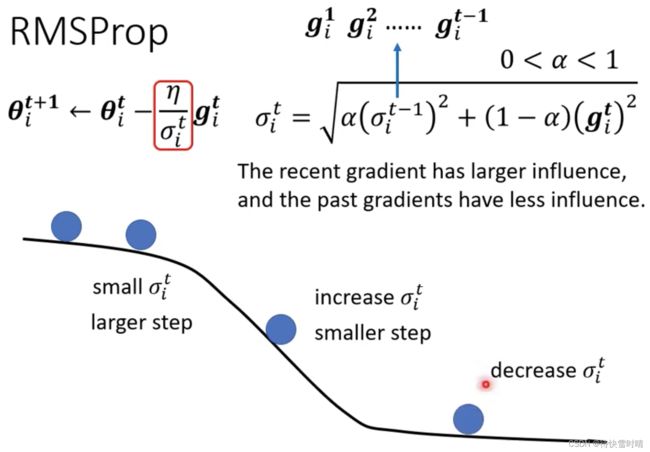
最常用的策略:Adam=RMSProp + Momentum
Learning Rate Scheduling
让学习率与时间有关。
Learning Rate Decay
随着时间不断前进,参数不断更新, 学习率越来越小 。
理解:因为我们一开始距离终点很远,随着我们离终点越来越近,就把学习率减小,让参数更新慢下来。
Warm up
让 学习率先变大后变小 。
理解: σ \sigma σ是一个统计的结果,只有数据越多才越精准。一开始学习率比较小,可以收集一些有关error surface的情报,并且限制参数不会离初始地方太远;等到 σ \sigma σ统计得比较精准以后,再让学习率慢慢爬升。
总结
- 使用动量,考虑过去梯度的大小与方向。
- 引入 σ \sigma σ,考虑过去梯度的大小 (RMS)。
- 使用Learning Rate Schedule。
批次标准化(Batch Normalization)简介
因为Error Surface崎岖的时候比较难训练,我们之前介绍的 自适应学习率 的方法,相当于是在难走的山路周围开辟一条路。那么有没有可能直接“铲平”崎岖的山脉⛰️呢?
Changing Landscape
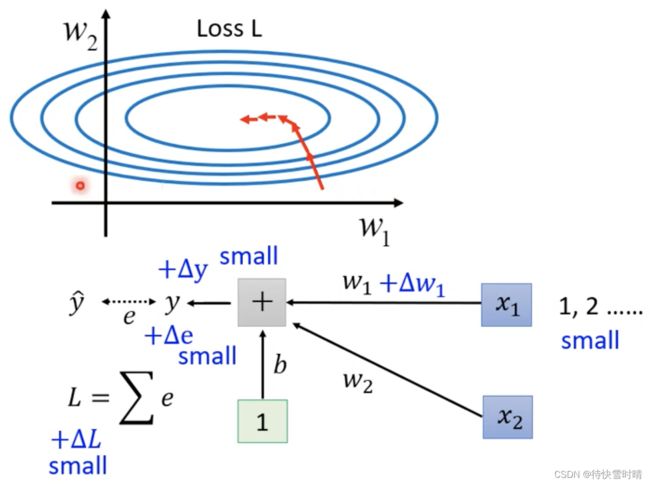
情况1: x 1 x_1 x1的值很小时,当权重参数 w 1 w_1 w1有一个很小的变化,此时对 y y y的影响很小,从而对损失Loss的影响也较小。
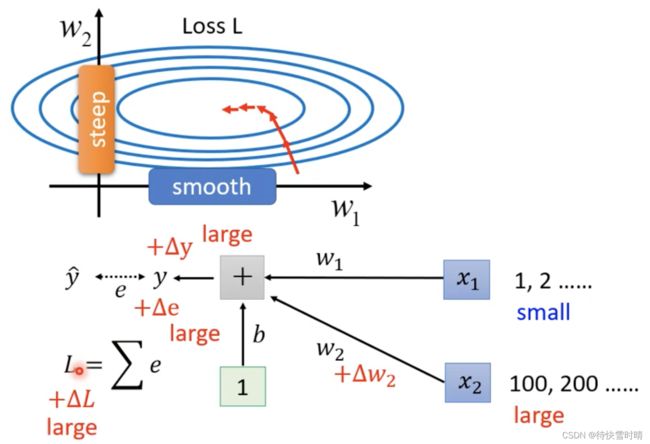
情况2: x 2 x_2 x2的值很大时,当权重参数 w 2 w_2 w2有一个很小的变化,也会因为乘上了大数值 x 2 x_2 x2而对 y y y的影响很大,从而使得 e e e变化很大,即对Loss的影响也很大。
结论
不同维度(Dimension)的输入值,大小的尺度(Scale)差距很大时,就可能产生在不同方向上,斜率、坡度非常不同的Error Surface。
解决方法:Feature Normalization
给不同的 dimension同样的数值范围 → \rightarrow → Feature Normalization(特征归一化)
假设 x 1 x^1 x1到 x R x^R xR是我们所有训练资料的特征向量,全部集合起来,对 同一个维度 中不同笔资料的特征值进行归一化。
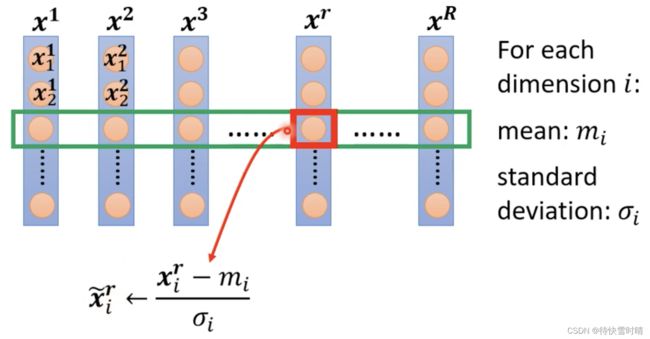
优点:
做完归一化之后,这个维度上的平均数值为0,方差为1,所以这排数值的分布在0上下。同样地,对每一个维度都做一样的归一化,就会发现所有特征在不同维度上的数值都在0左右,可以做出比较平坦的error surface,对训练有帮助,可以让梯度下降的收敛更快。
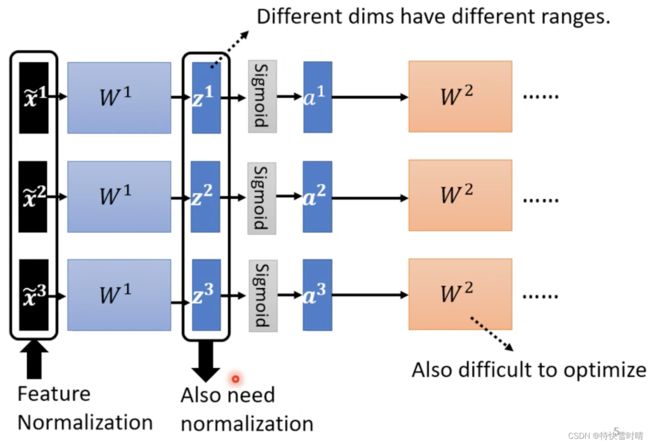
深度学习中的应用
值得注意的是,对于 W 2 W^2 W2来说, a 1 a^1 a1到 a 3 a^3 a3、 z 1 z^1 z1到 z 3 z^3 z3其实也是另一种输入。这是因为当 x ~ 1 \tilde{x}^1 x~1经过 W 1 W^1 W1矩阵后, a 1 , z 1 a^1,z^1 a1,z1数值的分布各维度仍然有很大的差异,要训练第二层的参数 W 2 W^2 W2,也会有困难,所以需要对 a a a或 z z z(也是一种特征值)进行归一化。
通常而言,归一化放在激活函数之前或者之后都是可以的。
如果选择Sigmoid,则推荐对 z z z做特征归一化,因为Sigmoid函数在0附近的斜率比较大,把所有值挪到0附近再计算梯度,算出的值会比较大。
具体计算步骤
-
把 z z z视作特征向量,分别取出对应的元素 z 1 , z 2 , z 3 z^1,z^2,z^3 z1,z2,z3,计算平均值和标准差,求得向量 μ , σ \mu,\sigma μ,σ。
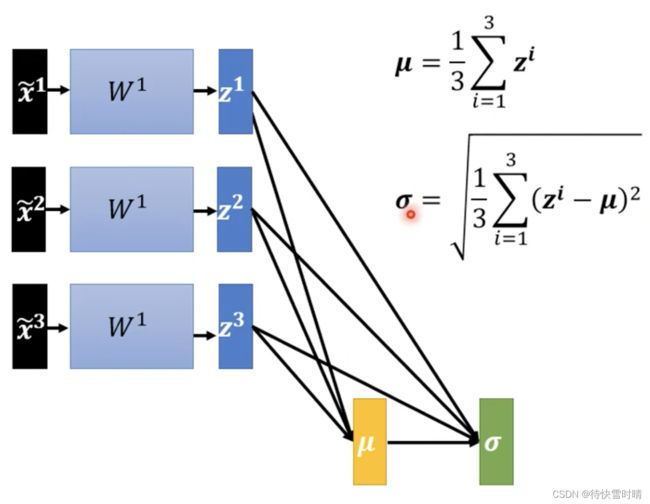
-
对每个向量 z z z,利用 μ , σ \mu,\sigma μ,σ对对应的元素进行归一化,得到 z ~ \tilde{z} z~.
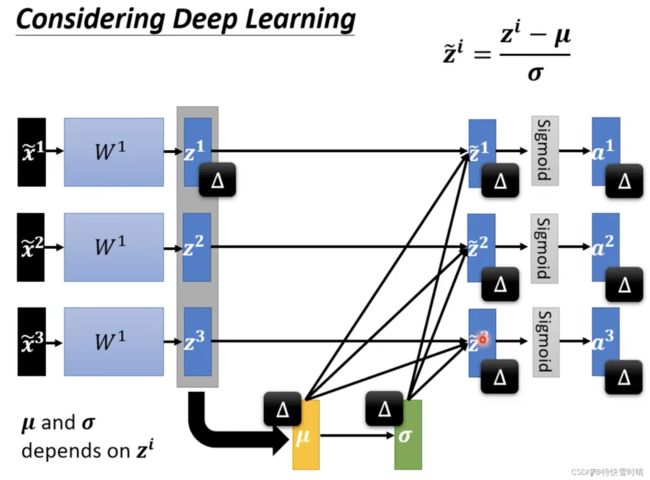
-
继续后续的步骤。
理解:对一批 z z z数据进行归一化 → \rightarrow → “网络”模型变为能够一次处理“一批 x x x数据”的模型,计算 μ , σ \mu,\sigma μ,σ,然后产生“一堆输出”,这时数据之间相互关联。
那么如何处理上百万笔数据资料呢?考虑使用有限数量的数据 → \rightarrow → 批次标准化(Batch Normalization)。
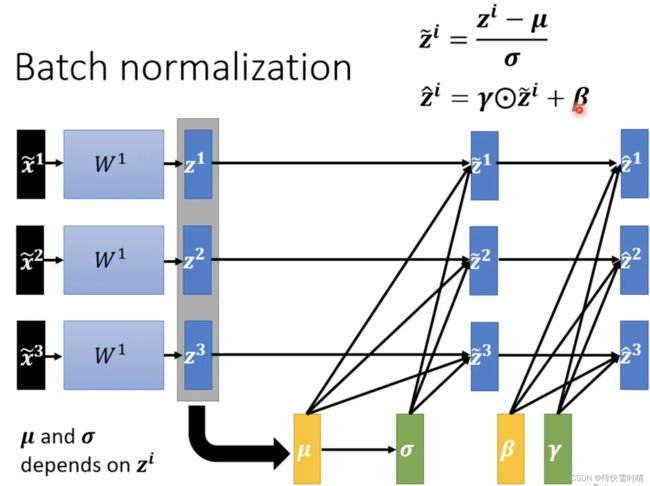
批次标准化(Batch Normalization)
定义:考虑一个batch内的数据做normalization,近似使用整个数据集。
适用场景:batch size比较大的时候,这时的数据可以认为足以表示整个数据集的分布,从而对整个数据集做Feature Normalization与在一个batch中做Feature Normalization是近似的。
显而易见,当我们做完标准化操作后, z ~ \tilde{z} z~的平均一定是0,可以看作是给这个神经网络的一些限制,这种限制可能会造成负面影响,所以我们要进行 恢复 操作,让模型另外学习参数 γ , β \gamma,\beta γ,β,使得原本被归一化的数据恢复到某一分布。
引入 γ , β \gamma,\beta γ,β还原归一化后的数据
- 初始值:将 γ \gamma γ设为全是1的向量, β \beta β设为全为0的向量。
- 让每一个维度的分布在刚开始训练时是比较接近的。
- 训练一段时间后,找到一个较好的error surface,再把参数值慢慢加进去。
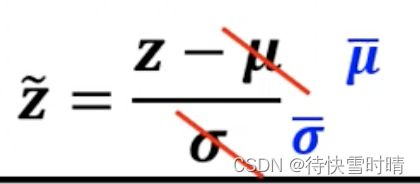
Testing(inference)时没有Batch进行标准化/归一化 → \rightarrow → 训练时会找到 μ ˉ , σ ˉ \bar{\mu},\bar{\sigma} μˉ,σˉ
问题 :在做作业时我们有完整的训练数据,可以分batch来计算均值和标准差。但是在实际的online project中,数据不是一下子可以提供完整的,这时我们不能说等待一个batch(比如说是batchsize=64)64笔数据资料都上传了才开始计算,而是要从一开始就计算。那么这个时候的均值和标准差如何计算?
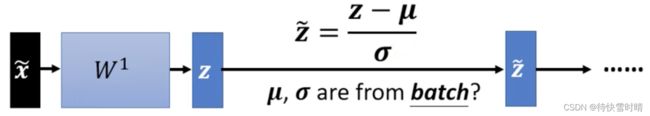
解决方法 :在训练的时候,每一个batch计算出来的均值和标准差,都会拿出来计算移动平均数(moving average)。p是超参数,需要自己定义。
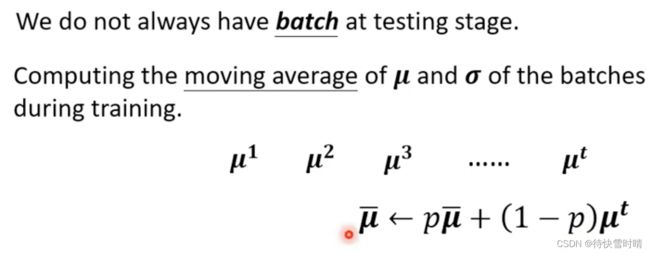
分类问题的损失函数
把分类(Classification)当作回归(Regression)来看
假设Class 1是编号1,Class 2是编号2,Class 3是编号3,希望模型的输出 y y y可以和Class的编号越接近越好。
以上的假设背后隐含着:Class 1和Class 2比较接近,Class 1和Class 3比较远。如果类别之间有某种联系,假设可能成立;如果类别之间没有特定关系,那么假设是错误的。因此我们引入第一节提到的 one-hot vector 。
Class as one-hot vector
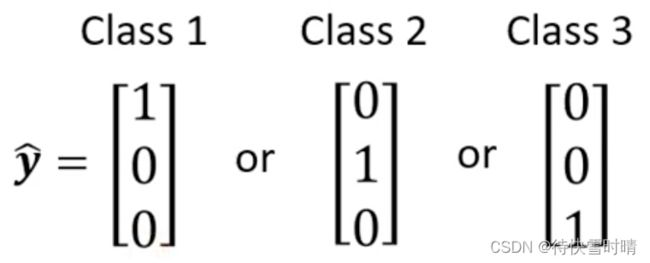
此时任意两个分类的距离都相同。我们根据上述向量的表示形式,来产生多个数值。
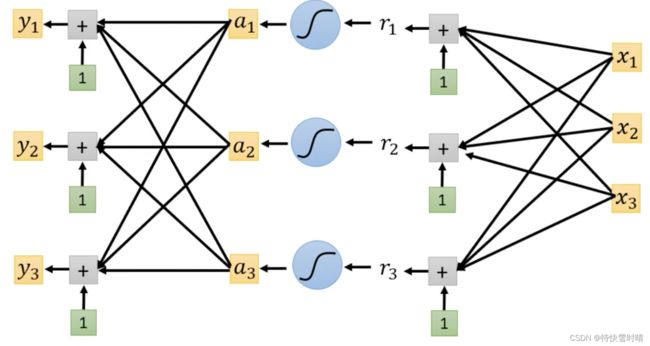
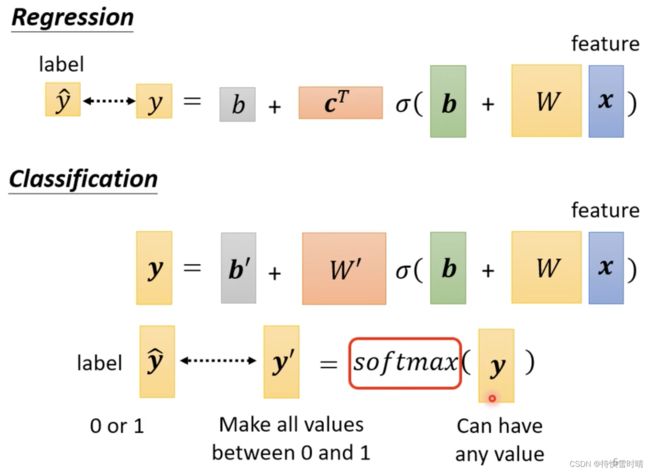
Classification with softmax
我们的目标只有0和1,但 y y y可能是任意值,因此我们使用 softmax把 y y y归一化,使之介于0到1之间 ,这样便于跟label计算相似度。
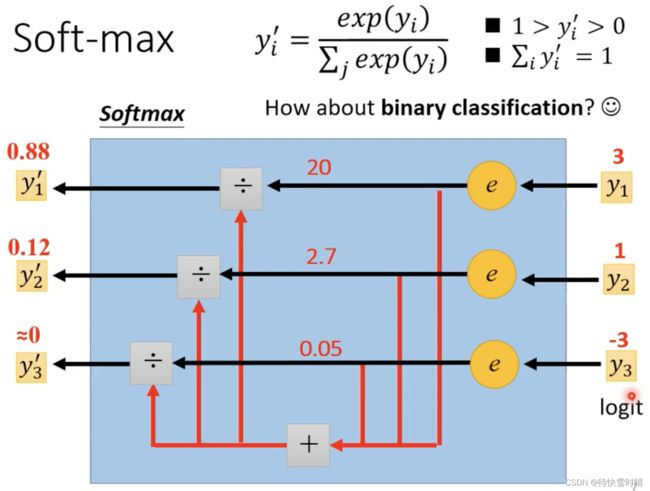
Soft-max内部运作模式
通过计算:
- 输出值变成介于0和1之间的数
- 输出值的和是1
- 原本大数值和小数值之间的 差距变得更大
Soft-max的输入经常称之为 Logit 。
关于二分类问题
使用sigmoid和使用softmax是等价的,同一件事情。
分类的损失函数
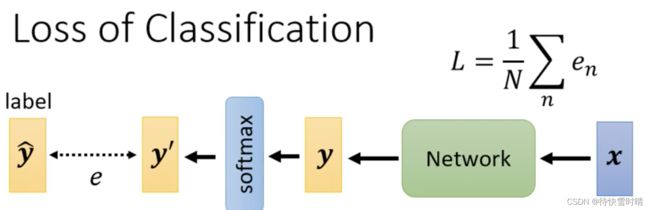
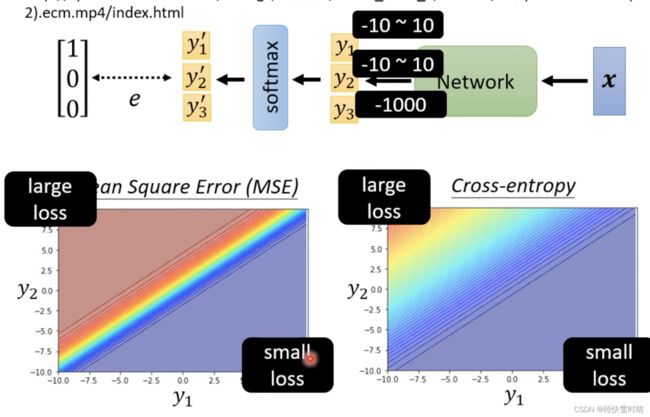
优化目标
减小 y ^ \hat{y} y^和 y ′ y^{'} y′之间的差距 e e e。
计算方法
交叉熵(等价于最大似然估计,见南瓜书)比均方差更适用于分类问题。
在Pytorch中,softmax被内建在Cross-enrtopy损失函数中。
举例
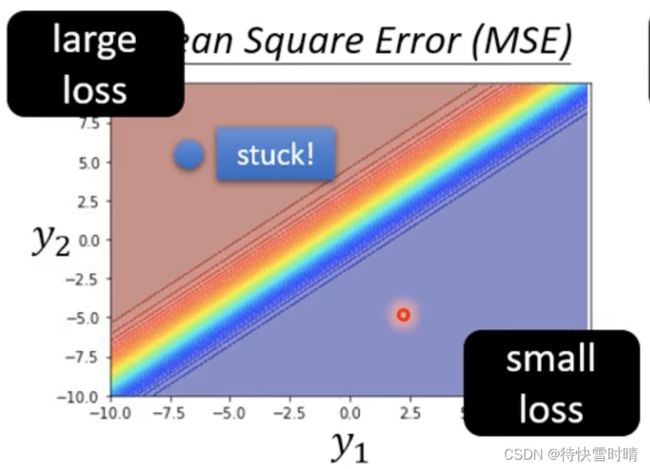
左上角loss大,右下角loss小,所以目标是从左上角走到右下角。
假设我们都从左上角开始,
Cross-entropy :左上角有斜率,可以透过梯度,一路往右下角走。更易收敛。
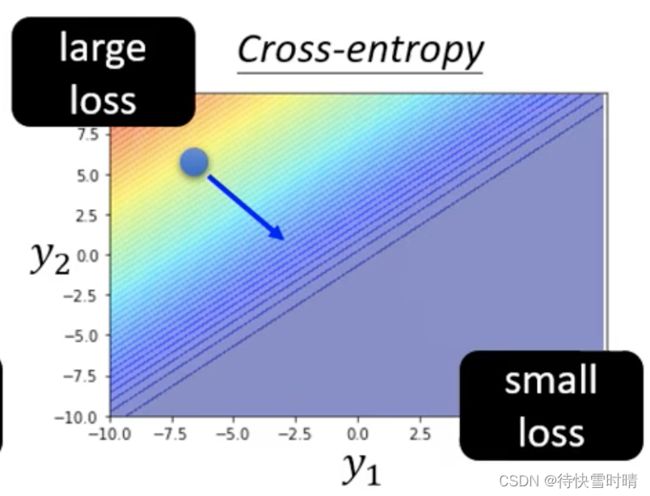
MSE :MSE在loss大的地方非常平坦,梯度趋近于零,最后stuck卡住!难以优化。
结论
改变损失函数,可能影响训练的过程。