判断二叉树是否为完全二叉树

判断二叉树是否为完全二叉树？

提示：本节仍然是重点说二叉树的DP递归套路，非常重要而且容易理解

二叉树的动态规划树形DP递归套路系列文章有这些，可以帮助你快速掌握树形DP的题目解题思想，就一个套路：
（1）判断二叉树是否为平衡二叉树？树形DP，树形动态规划的递归套路
（2）求二叉树中，任意两个节点之间的距离最大值是多少
（3）求二叉树中，包含的最大二叉搜索子树的节点数量是多少
（4）求二叉树中，包含的最大二叉搜索子树的头节点是谁，它包含的节点数量是多少
（5）求公司派对的最大快乐值
（6）判断二叉树是否为满二叉树

---

题目

给你一颗二叉树，请你判断二叉树是否为完全二叉树？

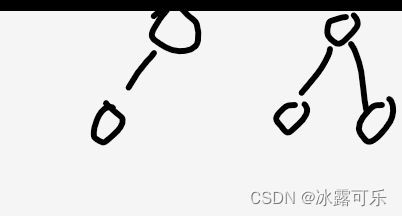
所谓完全二叉树，就是一颗二叉树，从左往右是依次变满的过程，即任何节点左右子尽量是双全的，不行就让左子全，右子不全，否则自己就是叶节点。
比如：

---

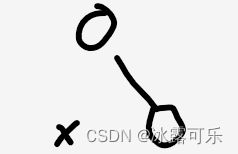
一、审题

示例：下面这个就不是完全二叉树，从左往右，缺了左。

本节用的二叉树是：

public static class Node {
        public int value;
        public Node left;
        public Node right;

        public Node(int v) {
            value = v;
        }
    }

    //构造一颗树，今后方便使用
    public static Node generateBinaryTree() {
        //树长啥样呢
        //          1
        //        2   3
        //       4 5 6 7
        //      8
        //     9
        Node head = new Node(1);
        Node n2 = new Node(2);
        Node n3 = new Node(3);
        head.left = n2;
        head.right = n3;
        Node n4 = new Node(4);
        Node n5 = new Node(5);
        n2.left = n4;
        n2.right = n5;
        Node n6 = new Node(6);
        Node n7 = new Node(7);
        n3.left = n6;
        n3.right = n7;
        Node n8 = new Node(8);
        n4.left = n8;
//        Node n9 = new Node(9);
//        n8.left = n9;
        return head;
    }

---

二、树形动态规划的递归套路：树形DP

95%的二叉树动态规划问题，都可以用以下套路解决：
一、定义个信息类：Info
收集x左树和右树都有的信息（左右树都有哦，而不是针对某单独的左树或者右树），比如是否平衡？树的高度，总之就是有的信息，不管你是String还是Boolean还是Integer类型的信息。经常是要讨论与x有关，还是 与x无关。

二、树形DP递归套路： 来到x节点
1）base case：考虑叶节点应该返回的信息Info
2）先收集左树和右树的信息Info
3）综合2）整理x自己的信息，并返回；

三、从题目给的二叉树head开始求（2），得到了一个head的信息Info，找里面咱们要用的那个信息：比如是否平衡？返回它。

来，咱们举例说明：实践知真理！

---

三、啥是完全二叉树？搞懂完全二叉树的本质很重要！

实际上，咱们要真的理解，并用实际的定义来记住完全二叉树的本质：
也就是，什么条件下，它不是完全二叉树，什么条件下，它才是完全二叉树，得撸清楚这俩条件，代码才能准确地判断！！！

所谓从左往右依次变满的过程：自然是二叉树的BFS遍历。

实际上，完全二叉树，它是根据满二叉树来定义的
——啥是满二叉树，就是节点个数N与层数k满足：N=2^k - 1的关系的树，说白了，最后一层节点全部要满。

上一篇文章我才写过：
（6）判断二叉树是否为满二叉树

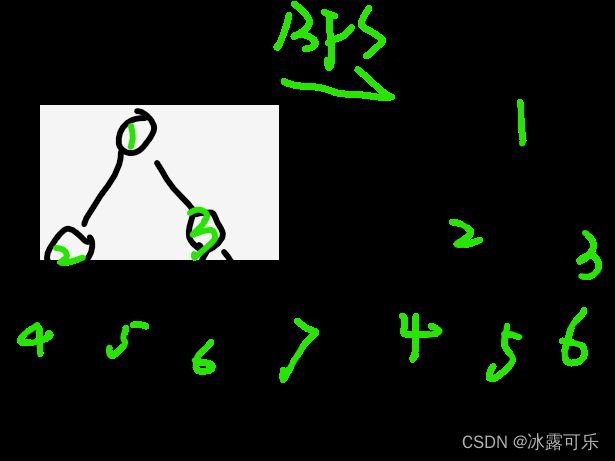
——啥样的二叉树是完全二叉树呢？
就是它的编号，从左往右依次完全对上满二叉树的编号，你要是缺了编号，可以，但是至少左边要对上，右边缺。
像下面这样：

四、笔试解：BFS判断的解题思路（用队列：额外空间）

那么代码中如何模拟这个过程呢？
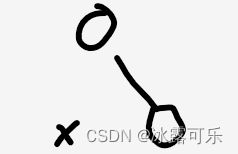
BFS遍历判断，就2个条件：
（1）如果某一个节点，它缺左树，但是有右树，一定不是完全二叉树！

（2）如果一个节点，它有左树，但是没有右树，则此时从左往右依次变满，这个节点右树往右今后都不再满了，
所以要求从此后遇到的所有节点，都得是叶节点，才能保证左边是满的过程。
所谓叶节点，就是左右子均为null的节点。

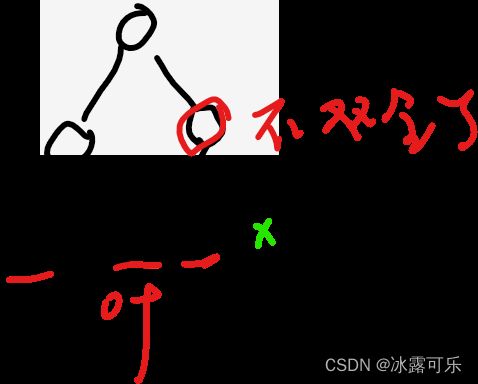
就这俩情况。
这就是BFS判断完全二叉树的2个条件。中间只需要用一个标志位，记录，我目前见过的cur节点，左右子是否为双全？
一旦遇到不双全了，此后遇到的节点，都得是叶节点。

先别看本节三的代码，先看看下面的五节，再深度理解一下完全二叉树的判断条件，不用BFS咋判断？那是面试代码
咱们先别手撕上面的代码！看下面的四 ，咱们来看看如果不用BFS，毕竟BFS要用队列，申请额外空间
如果不用BFS，只用二叉树的动态规划递归套路（树形DP），如何判断完全二叉树？

手撕BFS判断完全二叉树的代码：【本节代码适用于笔试AC】

//复习：透彻理解完全二叉树的本质，并理解BFS实现判断的原理，就俩条件一个标志
    public static boolean reviewIsCBT(Node head){
        if (head == null) return true;//空即满二叉树，满二叉树必然是完全二叉树

        //宏观调度为BFS代码
        Queue<Node> queue = new LinkedList<>();
        queue.add(head);
        //标志，先默认节点是双全的（左右子都有）
        boolean ownSon = false;

        while (!queue.isEmpty()){
            Node cur = queue.poll();
            Node left = cur.left;
            Node right = cur.right;

            //补充判断2条件--BFS判断，
            //如果有右子，没有左子，不行
            if (left == null && right != null) return false;
            //如果在已经不双全的情况下，cur不是叶节点，不行
            if (ownSon && !(left == null && right == null)) return false;

            if (left != null){
                queue.add(left);
            }
            if (right != null){
                queue.add(right);
            }
            if (left == null || right == null) ownSon = true;//尤其1为空，则从此不双全了。缺孩子
        }

        //全部判断完成都逃脱了，说明是满二叉树
        return true;
    }

    //树长啥样呢
    //          1
    //        2   3
    //       4 5 6 7
    //      8
    public static void test(){
        Node cur = generateBinaryTree();//一个树
        boolean isCBT = isCBT1(cur);
        System.out.println(isCBT);

        boolean isCBT2 = reviewIsCBT(cur);
        System.out.println(isCBT2);
    }

结果没问题：true
反正搞清楚BFS遍历的判断条件，很重要。

---

五、面试最优解：树形DP的递归套路，o(1)空间复杂度。

上面咱们介绍BFS判断啥样的二叉树是完全二叉树

就是它的编号，从左往右依次完全对上满二叉树的编号，你要是缺了编号，可以，但是至少左边要对上，右边缺。
像下面这样：

现在咱不用BFS，单纯用二叉树的动态规划递归套路（树形DP）来判断二叉树是否为完全二叉树？
和满二叉树有关系：
不妨设：x左树高度为h1，右树高度为h2

（1）如果左树是满二叉树，右树也是满二叉树，则x必然是满二叉树，x也必然是完全二叉树！！！
为啥呢？
我们完全二叉树，就是根据满二叉树定义来的哇！
完全二叉树从左往右编号就是要完全对上满二叉树，必然，满二叉树就是一个特定完美的完全二叉树

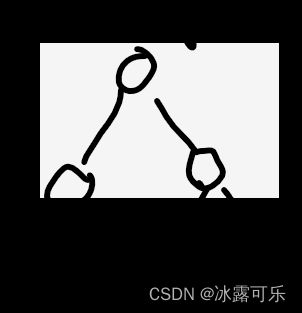
哦！
你看真的是这样吗？？？？？？？？
如果二叉树x它不是满二叉树呢？？？下面这个，左右都是满二叉树，你要注意了，则必然要求h1=h2+1，这样才是完全二叉树！

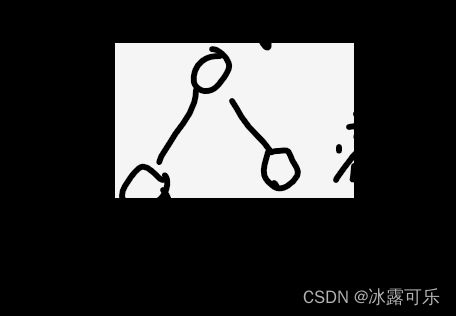
这一步一定要小心哦！！！！！
在代码中，这样子安排，如果x是满二叉树，其他几个条件必然不用判断了，直接确定x就是满二叉树
如果x确定不是满二叉树了，则判断其他几个条件，慢慢确认。

（2）如果左树是满二叉树，右树也是完全二叉树，则要求h1=h2，这样才能使得x是完全二叉树。

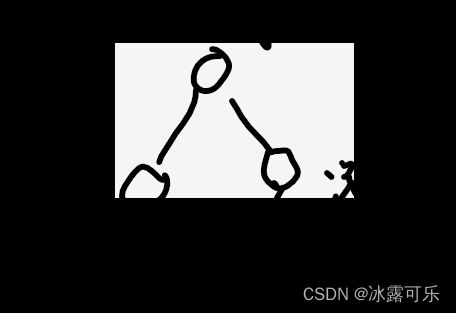
（3）如果左树是完全二叉树，右树也是满二叉树，则要求h1=h2+1，左边完全，右边就必须是满，自然h2矮一层。
这也是BFS那就说过了，从左往右依次变满，h1那不满，h2满，短一截。

（4）左边是完全二叉树，右边也是完全二叉树？不可能，它一定不是完全二叉树

OK，就这么几个情况。
这下你明白啥是完全二叉树了吧？

咱们利用树形DP，其实，说完上面4个定义条件，我们已经知道如何整合信息了，现在确定一下：看看要收集哪些信息？

到这里可以先回到四，去看看BFS的手撕代码，那个代码简单，适用于笔试AC，面试可用这个树形DP的递归套路，作为最优解

95%的二叉树动态规划问题，都可以用以下套路解决：
一、定义个信息类：Info
收集x左树和右树都有的信息（左右树都有哦，而不是针对某单独的左树或者右树），比如是否平衡？树的高度，总之就是有的信息，不管你是String还是Boolean还是Integer类型的信息。经常是要讨论与x有关，还是 与x无关。
这里永远与x有关
本题中，上面几个条件，看出，咱需要收集树的高度信息height
咱还需要判断x是不是满二叉树？isFBT ，isFullBinaryTree缩写
这个信息从下往上判断的过程，就有了，有左子，有右子，且左右都是满二叉树的情况下，左右树高度一样，isFBT=true。
虽然之前我们求满二叉树，是通过该记录N和层数k，这里不需要了。
咱还要判断一个树是否是完全二叉树，isCBT，isCompleteBinaryTree的缩写。这本身就是咱这一题要求的，需要下面整理。
所以我们的信息类，需要记录仨东西：

 public static class Info{
        public boolean isCBT;//完全二叉
        public boolean isFBT;//满二叉
        public int height;//高度
        public Info(int h, boolean CBT, boolean FBT){
            height = h;
            isCBT = CBT;
            isFBT = FBT;
        }
    }

二、树形DP递归套路： 来到x节点
根据上面的分析
咱们定义个函数f(Node x),收集x所需要的信息Info

1）base case：考虑叶节点应该返回的信息Info
叶节点的null，自然高度0，是满二叉树，也会是完全二叉树，

if (head == null) return new Info(0, true, true);//null，就是

2）先收集左树和右树的信息Info
好说：

        //两边收集信息
        Info leftInfo = process(head.left);
        Info rightInfo = process(head.right);

3）综合2）整理x自己的信息，并返回；
——高度height嘛，左右树最高的+1（x自己）
——是否完全二叉树？只要左右都是满二叉树的情况下，左右树高度一样，isFBT=true
——是否完全二叉树？
（1）如果x的isFBT=true，则isCBT=true，直接返回
不满足（1）则下面几个情况分开讨论：
（2）左右都是满二叉树，你要注意了，则必然要求h1=h2+1，这样才是完全二叉树！

（3）如果左树是满二叉树，右树也是完全二叉树，则要求h1=h2，这样才能使得x是完全二叉树。

（4）如果左树是完全二叉树，右树也是满二叉树，则要求h1=h2+1，左边完全，右边就必须是满，自然h2矮一层。
这也是BFS那就说过了，从左往右依次变满，h1那不满，h2满，短一截。

（5）左边是完全二叉树，右边也是完全二叉树？不可能，它一定不是完全二叉树

好，理解了完全二叉树的定义和判断条件，手撕代码非常容易，收集信息：

//复习：树形DP判断完全二叉树，整理信息：
    public static Info f(Node x){
        if (x == null) return new Info(0, true, true);

        //左右收集
        Info left = f(x.left);
        Info right = f(x.right);

        //整理
        int height = Math.max(left.height, right.height) + 1;
        boolean isFBT = left.isCBT && right.isCBT && (left.height == right.height);
        boolean isCBT = false;//先默认false非完全二叉树

        if (isFBT) isCBT = true;//直接走人.（1）如果x的isFBT=true，则isCBT=true，直接返回
        else {
            //不是满二叉树，才需要走这几个条件--记不住，理解这个定义，画图看，到时候
            //（2）左右都是满二叉树，你要注意了，则必然要求h1=h2+1，这样才是完全二叉树！
            if (left.isFBT && right.isFBT && left.height == right.height + 1) isCBT = true;
            //（3）如果左树是满二叉树，右树也是完全二叉树，**则要求h1=h2**，这样才能使得x是完全二叉树。
            if (left.isFBT && right.isCBT && left.height == right.height) isCBT = true;
            //（4）如果左树是完全二叉树，右树也是满二叉树，则要求h1=h2+1
            if (left.isCBT && right.isFBT && left.height == right.height + 1) isCBT = true;
            //（5）左边是完全二叉树，右边也是完全二叉树？不可能，它一定不是完全二叉树
            //默认就是false不管
        }

        return new Info(height, isCBT, isFBT);//前后顺序别乱
    }

三、从题目给的二叉树head开始求（2），得到了一个head的信息Info，找里面咱们要用的那个信息：比如是否平衡？返回它。
调用嘛很简单：

//调用
    public static boolean reviewIsFBTFace(Node head){
        if (head == null) return true;
        
        Info info = f(head);
        return info.isCBT;
    } 

测试一把：

public static void test2(){
        Node cur = generateBinaryTree();
        boolean isCBT = isCBT2(cur);
        System.out.println(isCBT);

        isCBT = reviewIsFBTFace(cur);
        System.out.println(isCBT);
    }
    //树长啥样呢
    //          1
    //        2   3
    //       4 5 6 7
    //      8

    public static void main(String[] args) {
//        test();
        test2();
    }

太累的时候，容易写错代码，自己检查一下。
666
结果：

true
true

很牛吧，相信你搞懂完全二叉树的本质之后，就非常容易了

---

总结

提示：重要经验：

1）完全二叉树的定义是根据满二叉树来的，希望从左往右编号能跟满二叉树对应上，缺只能缺右边，不能缺左边。
2）判断完全二叉树的2个方法，一个事BFS遍历判断，就2个条件，关键看节点是否双全，第一次遇到不双全，今后都得是叶节点，第二个方法是树形DP，画图看看完全二叉树的几个条件。就明白了，自己要理解透彻。
3）笔试求AC，可以不考虑空间复杂度，但是面试既要考虑时间复杂度最优，也要考虑空间复杂度最优。