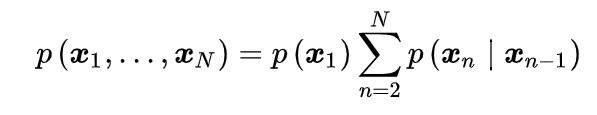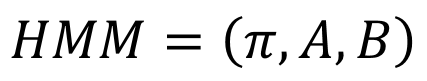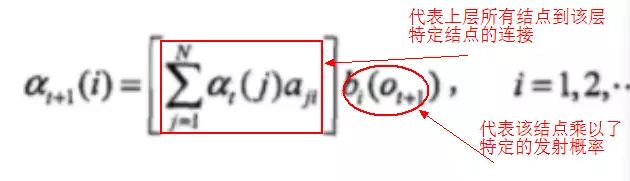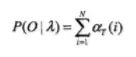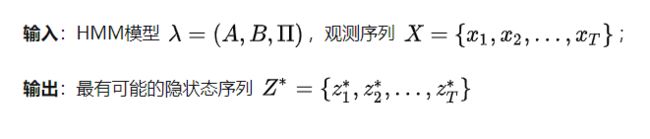学习笔记——详解马尔可夫，马尔可夫链，马尔可夫模型，隐马

目录

（一），马尔可夫 （Markov）综述

1.1，随机过程是啥玩意儿

1.2. 马尔可夫链 （Markov Chain）又是什么鬼

1.3一个经典的马尔科夫链实例 

（二）， 隐马尔可夫 HMM

2.1马尔可夫引言 

 2.2下边是隐马尔可夫

3，HMM解决的三个问题

定义HMM中用到的变量（2.1节适用）

​

3.1观测序列概率

（3.1.1）暴力解法

 （3.1.2）. 前向后向算法：

前向算法 :

后向算法 ：

总结：

观测序列概率 Python 实现

3.2HMM 参数学习

（3.2.1）. 鲍姆-韦尔奇算法原理

 （3.2.2）. 鲍姆-韦尔奇算法推导

3.3，HMM 解码问题

（3.31）. HMM 解码问题概述

（3.3.2）. 维特比算法流程

 （3.3.3）HMM 解码 Python 实现

总结 ：

（三）马尔可夫随机场 MRF及命名实体识别

（1）什么叫随机场？

(2)命名实体识别入门案例

---

（一），马尔可夫 （Markov）综述

引例：假设我们观测⼀个⼆值变量，这个⼆值变量表⽰某⼀天是否下⾬。给定这个变量的⼀系列观测，我们希望预测下⼀天是否会下⾬。

• 如果我们将所有的数据都看成独⽴同分布的， 那么我们能够从数据中得到的唯⼀的信息就是⾬天的相对频率；
• 然而，我们知道天⽓经常会呈现出持续若⼲天的趋势。因此，观测到今天是否下⾬对于预测明天是否下⾬会 有极⼤的帮助。

我们可以使用概率的乘积规则来表示观测序列的联合概率分布，形式为

利用马尔科夫性，可以将上式变为⼀阶马尔科夫链（first-order Markov chain）：

根据我们在概率图模型中讲的 d-分离 性质，观测  的条件概率分布为

当然了，还可以有⼆阶马尔科夫链，其中特定的观测依赖于前两次观测和的值：

还有M阶马尔可夫链，当然计算代价也很大：

1.1，随机过程是啥玩意儿

讲马尔可夫链不得不提到随机过程，因为它是随机过程课本中的，啊啊。

顾名思义，它其实就是个过程，比如今天下雨，那么明天下不下雨呢？后天下不下雨呢？从今天下雨到明天不下雨再到后天下雨，这就是个过程。那么怎么预测N天后到底下不下雨呢？这其实是可以利用公式进行计算的，随机过程就是这样一个工具，把整个过程进行量化处理，用公式就可以推导出来N天后的天气状况，下雨的概率是多少，不下雨的概率是多少。说白了，随机过程就是一些统计模型，利用这些统计模型可以对自然界的一些事物进行预测和处理，比如天气预报，比如股票，比如市场分析，比如人工智能。它的应用还真是多了去了。

话说回来，还真是佩服能构造出这些统计模型的大牛，简直脑洞大开啊。

---

1.2. 马尔可夫链 （Markov Chain）又是什么鬼

好了，终于可以来看看马尔可夫链 （Markov Chain）到底是什么了。

它是随机过程中的一种过程，到底是哪一种过程呢？好像一两句话也说不清楚，还是先看个例子吧。

先说说我们村智商为0的王二狗，人傻不拉几的，见人就傻笑，每天中午12点的标配，仨状态：吃，玩，睡。这就是传说中的状态分布。

你想知道他n天后中午12点的状态么？是在吃，还是在玩，还是在睡？这些状态发生的概率分别都是多少？ （知道你不想，就假装想知道吧~~学习真的好累~~）

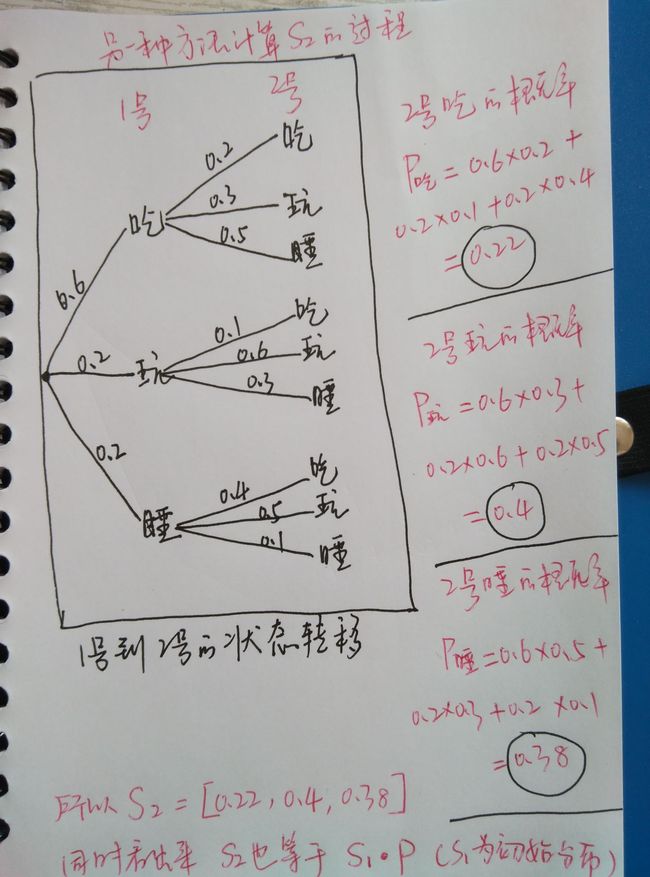
先看个假设，他每个状态的转移都是有概率的，比如今天玩，明天睡的概率是几，今天玩，明天也玩的概率是几几，看图更清楚一点。

这个矩阵就是转移概率矩阵P，并且它是保持不变的，就是说第一天到第二天的转移概率矩阵跟第二天到第三天的转移概率矩阵是一样的。（这个叫时齐，不细说了，有兴趣的同学自行百度）。

有了这个矩阵，再加上已知的第一天的状态分布，就可以计算出第N天的状态分布了。

S1 是4月1号中午12点的的状态分布矩阵 [0.6, 0.2, 0.2]，里面的数字分别代表吃的概率，玩的概率，睡的概率。

那么

4月2号的状态分布矩阵 S2 = S1 * P (俩矩阵相乘)。

4月3号的状态分布矩阵 S3 = S2 * P (看见没，跟S1无关，只跟S2有关)。

4月4号的状态分布矩阵 S4 = S3 * P (看见没，跟S1，S2无关，只跟S3有关)。

...

4月n号的状态分布矩阵 Sn = Sn-1 * P (看见没，只跟它前面一个状态Sn-1有关)。

总结：马尔可夫链就是这样一个任性的过程，它将来的状态分布只取决于现在，跟过去无关！

就把下面这幅图想象成是一个马尔可夫链吧。实际上就是一个随机变量随时间按照Markov性进行变化的过程。

=================================更新============

附：S2 的计算过程 (没兴趣的同学自行略过)

原文链接https://zhuanlan.zhihu.com/p/26453269 

1.3一个经典的马尔科夫链实例 

用一句话来概括马尔科夫链的话，那就是某一时刻状态转移的概率只依赖于它的前一个状态。举个简单的例子，假如每天的天气是一个状态的话，那个今天是不是晴天只依赖于昨天的天气，而和前天的天气没有任何关系。这么说可能有些不严谨，但是这样做可以大大简化模型的复杂度，因此马尔科夫链在很多时间序列模型中得到广泛的应用，比如循环神经网络RNN，隐式马尔科夫模型HMM等。
假设状态序列为⋯ x t − 2 , x t − 1 , x t , x t + 1 , x t + 2 , ⋯ ⋯ x t − 2 , x t − 1 , x t , x t + 1 , x t + 2 , ⋯ ⋯ x t − 2 , x t − 1 , x t , x t + 1 , x t + 2 , ⋯ ⋯xt−2,xt−1,xt,xt+1,xt+2,⋯⋯xt−2,xt−1,xt,xt+1,xt+2,⋯ \cdots x_{t-2}, x_{t-1}, x_t, x_{t+1}, x_{t+2}, \cdots⋯xt−2,xt−1,xt,xt+1,xt+2,⋯⋯xt−2,xt−1,xt,xt+1,xt+2,⋯⋯xt−2​,xt−1​,xt​,xt+1​,xt+2​,⋯t0​=[0.1,0.2,0.7]，然后算之后的状态。 

def markov():
    init_array = np.array([0.1, 0.2, 0.7])
    transfer_matrix = np.array([[0.9, 0.075, 0.025],
                               [0.15, 0.8, 0.05],
                               [0.25, 0.25, 0.5]])
    restmp = init_array
    for i in range(25):
        res = np.dot(restmp, transfer_matrix)
        print i, "\t", res
        restmp = res
markov()

结果：

0 	 [0.295  0.3425 0.3625]
1 	 [0.4075  0.38675 0.20575]
2 	 [0.4762 0.3914 0.1324]
3 	 [0.52039  0.381935 0.097675]
4 	 [0.55006  0.368996 0.080944]
5 	 [0.5706394 0.3566873 0.0726733]
6 	 [0.58524688 0.34631612 0.068437  ]
7 	 [0.59577886 0.33805566 0.06616548]
8 	 [0.60345069 0.33166931 0.06487999]
9 	 [0.60907602 0.32681425 0.06410973]
10 	 [0.61321799 0.32315953 0.06362248]
11 	 [0.61627574 0.3204246  0.06329967]
12 	 [0.61853677 0.31838527 0.06307796]
13 	 [0.62021037 0.31686797 0.06292166]
14 	 [0.62144995 0.31574057 0.06280949]
15 	 [0.62236841 0.31490357 0.06272802]
16 	 [0.62304911 0.31428249 0.0626684 ]
17 	 [0.62355367 0.31382178 0.06262455]
18 	 [0.62392771 0.31348008 0.06259221]
19 	 [0.624205  0.3132267 0.0625683]
20 	 [0.62441058 0.31303881 0.06255061]
21 	 [0.624563   0.31289949 0.06253751]
22 	 [0.624676  0.3127962 0.0625278]
23 	 [0.62475978 0.31271961 0.06252061]
24 	 [0.6248219  0.31266282 0.06251528]

从第18次开始，状态就开始收敛至[ 0.624 , 0.312 , 0.0625 ] [ 0.624 , 0.312 , 0.0625 ] [ 0.624 , 0.312 , 0.0625 ] [0.624,0.312,0.0625][0.624,0.312,0.0625] [0.624, 0.312, 0.0625][0.624,0.312,0.0625][0.624,0.312,0.0625][0.624,0.312,0.0625]P的幂次方有什么有意思的地方？废话不多说，直接上代码。

def matrixpower():
    transfer_matrix = np.array([[0.9, 0.075, 0.025],
                               [0.15, 0.8, 0.05],
                               [0.25, 0.25, 0.5]])
    restmp = transfer_matrix
    for i in range(25):
        res = np.dot(restmp, transfer_matrix)
        print i, "\t", res
        restmp = res
matrixpower()

结果：

0 	[[ 0.8275   0.13375  0.03875]
 [ 0.2675   0.66375  0.06875]
 [ 0.3875   0.34375  0.26875]]
1 	[[ 0.7745   0.17875  0.04675]
 [ 0.3575   0.56825  0.07425]
 [ 0.4675   0.37125  0.16125]]
2 	[[ 0.73555   0.212775  0.051675]
 [ 0.42555   0.499975  0.074475]
 [ 0.51675   0.372375  0.110875]]
3 	[[ 0.70683   0.238305  0.054865]
 [ 0.47661   0.450515  0.072875]
 [ 0.54865   0.364375  0.086975]]
4 	[[ 0.685609   0.2573725  0.0570185]
 [ 0.514745   0.4143765  0.0708785]
 [ 0.570185   0.3543925  0.0754225]]
5 	[[ 0.6699086  0.2715733  0.0585181]
 [ 0.5431466  0.3878267  0.0690267]
 [ 0.585181   0.3451335  0.0696855]]
6 	[[ 0.65828326  0.28213131  0.05958543]
 [ 0.56426262  0.36825403  0.06748335]
 [ 0.5958543   0.33741675  0.06672895]]
7 	[[ 0.64967099  0.28997265  0.06035636]
 [ 0.5799453   0.35379376  0.06626094]
 [ 0.60356362  0.33130471  0.06513167]]
8 	[[ 0.64328888  0.29579253  0.06091859]
 [ 0.59158507  0.34309614  0.06531879]
 [ 0.60918588  0.32659396  0.06422016]]
9 	[[ 0.63855852  0.30011034  0.06133114]
 [ 0.60022068  0.33517549  0.06460383]
 [ 0.61331143  0.32301915  0.06366943]]
10 	[[ 0.635052    0.30331295  0.06163505]
 [ 0.60662589  0.3293079   0.06406621]
 [ 0.61635051  0.32033103  0.06331846]]
11 	[[ 0.63245251  0.30568802  0.06185947]
 [ 0.61137604  0.32495981  0.06366415]
 [ 0.61859473  0.31832073  0.06308454]]
12 	[[ 0.63052533  0.30744922  0.06202545]
 [ 0.61489845  0.32173709  0.06336446]
 [ 0.6202545   0.31682232  0.06292318]]
13 	[[ 0.62909654  0.30875514  0.06214832]
 [ 0.61751028  0.31934817  0.06314155]
 [ 0.62148319  0.31570774  0.06280907]]
14 	[[ 0.62803724  0.30972343  0.06223933]
 [ 0.61944687  0.3175772   0.06297594]
 [ 0.6223933   0.3148797   0.062727  ]]
15 	[[ 0.62725186  0.31044137  0.06230677]
 [ 0.62088274  0.31626426  0.062853  ]
 [ 0.62306768  0.31426501  0.06266732]]
16 	[[ 0.62666957  0.31097368  0.06235675]
 [ 0.62194736  0.31529086  0.06276178]
 [ 0.62356749  0.31380891  0.0626236 ]]
17 	[[ 0.62623785  0.31136835  0.0623938 ]
 [ 0.6227367   0.31456919  0.06269412]
 [ 0.62393798  0.31347059  0.06259143]]
18 	[[ 0.62591777  0.31166097  0.06242126]
 [ 0.62332193  0.31403413  0.06264394]
 [ 0.62421263  0.31321968  0.0625677 ]]
19 	[[ 0.62568045  0.31187792  0.06244162]
 [ 0.62375584  0.31363743  0.06260672]
 [ 0.62441624  0.31303361  0.06255015]]
20 	[[ 0.6255045   0.31203878  0.06245672]
 [ 0.62407756  0.31334332  0.06257913]
 [ 0.62456719  0.31289565  0.06253716]]
21 	[[ 0.62537405  0.31215804  0.06246791]
 [ 0.62431608  0.31312525  0.06255867]
 [ 0.62467911  0.31279335  0.06252754]]
22 	[[ 0.62527733  0.31224646  0.06247621]
 [ 0.62449293  0.31296357  0.0625435 ]
 [ 0.62476209  0.3127175   0.06252042]]
23 	[[ 0.62520562  0.31231202  0.06248236]
 [ 0.62462404  0.3128437   0.06253225]
 [ 0.62482361  0.31266126  0.06251514]]
24 	[[ 0.62515245  0.31236063  0.06248692]
 [ 0.62472126  0.31275483  0.06252391]
 [ 0.62486922  0.31261956  0.06251122]]

从第20次开始，结果开始收敛，并且每一行都为[ 0.625 , 0.312 , 0.0625 ] [ 0.625 , 0.312 , 0.0625 ] [ 0.625 , 0.312 , 0.0625 ] [0.625,0.312,0.0625][0.625,0.312,0.0625] [0.625, 0.312, 0.0625][0.625,0.312,0.0625][0.625,0.312,0.0625][0.625,0.312,0.0625]π是方程

（二）， 隐马尔可夫 HMM

2.1马尔可夫引言 

为了方便引入前边得知识跟上边的马尔可夫一样，不感兴趣可以跳过 

马尔可夫模型(Markov Model)是通过寻找事物状态的规律对未来事物状态进行预测的概率模型，在马尔可夫模型中假设当前事物的状态只与之前的n个状态有关。n=1时表示事物当前的状态只与上一个状态有关，这也是最简单的一阶马尔可夫模型。隐马尔科夫模型(Hidden Markov Model)是马尔可夫模型中的一种。马尔可夫模型的使用场景非常广泛，包括语言识别，自然语言处理和生物信息领域。Google的PageRank算法中也使用到了马尔可夫模型。

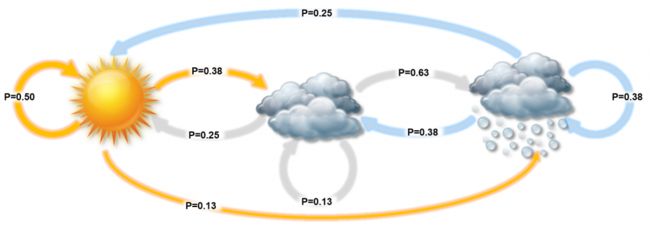
我们以天气预测的示例来说明马尔可夫模型和隐马尔可夫模型的作用。现实中每一天的天气状态都可能会不同，比如：晴天，多云，或是雷雨等。我们希望通过天气状态的变化规律生成一个模型对未来一天的天气状态进行预测。为了简化计算过程，只选择三种天气状态进行说明。通过观察，我们发现晴天，多云和雷雨三种天气状态间的变化概率。下图详细说明了每种天气状态之间相互转换的概率。

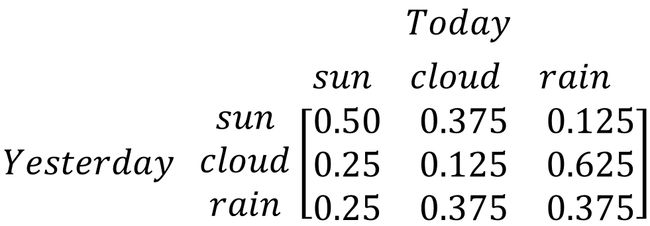
以晴天为例，假设每一天的天气状态只与前一天的天气状态有关(n=1)。如果第一天是晴天，那么第二天转换为多云的概率为0.38，转换为雷雨的概率为0.13，依旧是晴天的概率为0.50。晴天转换为这三种天气状态的概率的总和为1。下面我们通过概率矩阵列出了三种从昨天到今天三种天气状态之间的转换概率。注意，每一行的概率总和为1。

除了天气间状态转换概率，我们还需要一个初始概率，就是昨天的天气状态，这里假设昨天的天气状态是晴天。

到这里，我们定义了一个一阶的马尔可夫模型，分别为：

• 状态：晴天，多云，雷雨
• 状态转换概率：三种天气状态间的转换概率
• 初始概率：晴天

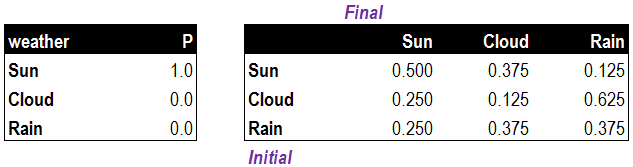
我们将马尔可夫模型转换为表格，用于计算今天天气状态的概率。昨天的天气状态为“晴天”，因此在第一个初始状态表中Sun的概率为1.0。转换概率表中，昨天为初始状态，今天为最终状态，相交处为初始天气状态到最终天气状态的转化概率。

通过初始状态和转换概率，我们可以求出今天三种天气状态发生的概率。并以概率最高的天气状况作为对今天天气的预测。下面列出计算今天(t=1)三种天气状况的公式：

• 今天为晴天的概率=初始晴天概率X晴天转晴天概率+初始多云概率X多云转晴天概率+初始雷雨概率X雷雨转晴天概率。
• 今天为多云的概率=初始晴天概率X晴天转多云概率+初始多云概率X多云转多云概率+初始雷雨概率X雷雨转多云概率。
• 今天为雷雨的概率=初始晴天概率X晴天转雷雨概率+初始多云概率X多云转雷雨概率+初始雷雨概率X雷雨转雷雨概率。

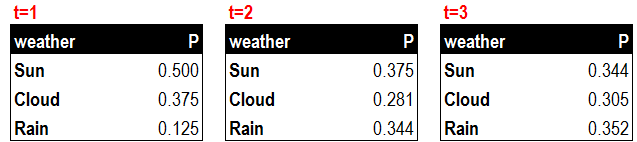
明天(t=2)的天气状况预测方法与今天(t=1)的类似，只不过初始概率变为了今天(t=1)。以下列出了今天(t=1)，明天(t=2)和后天(t=3)的天气状况预测数据。

在前面的例子中，我们可以直接观察到天气的情况，并且根据每一天的天气状况预测第二天的天气。 

---

 2.2下边是隐马尔可夫

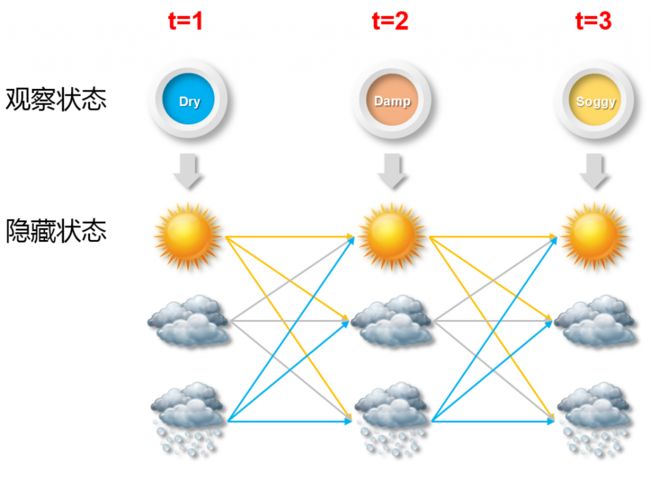
当我们无法直接获得天气状况，只能获得一些间接的信息时，就需要一个模型通过间接的信息来预测直接的信息了。这个模型就是隐马尔可夫模型(Hidden Markov Model)。在天气预测的例子中，水藻和天气状况的变化存在紧密的联系，如果我们不能直接获得每天的天气状况，就需要通过每天水藻的状态的变化来推测。下图显示了水藻的状态与天气状态的对应关系。其中水藻的状态为我们能看到的观察状态，天气状态为我们看不到的隐藏状态。

在隐马尔可夫模型中，有三个必须的元素，分别是初始概率(π)，转换概率矩阵(A)和对应概率矩阵(B)。初始概率和转换概率矩阵与前面的马尔可夫模型一样。对应概率矩阵是指观察状态与隐藏状态间的对应关系。在天气预测的例子中，就是水藻状态与天气状态间的对应概率。以下是隐马尔可夫模型的三元素。

第一个元素初始概率(π)，也就是昨天的天气状态我们设定为晴天，概率为1.0。

第二个元素(A)是天气状态间的转换概率，这里使用的数值和前面马尔可夫例子中的值是完全一样的。表示的意义也完全相同。

第三个元素(B)是观察状态与隐藏状态的对应概率矩阵，在天气预测的例子中就是水藻状态与天气状态对应概率矩阵，观察状态可能和隐藏状态的数量一致，也可能不一致。对应概率矩阵中显示了每一种水藻状态对应的天气状态概率，例如，当天气状态是晴天时，水藻为干燥的状态为0.6，微湿的概率为0.2，湿润的概率为0.15，湿透的概率为0.05。这些状态的汇总概率为1。

我们把隐马尔可夫模型中的三个元素转化为表格，根据观察状态推测哪一种隐藏状态出现的概率最大。简单来说就是根据水藻的不同状态再结合不同天气状态间的转换概率来推测未来三天的天气状态概率。

这里我们使用穷举的方法来找出概率最高的天气状态组合。下图中显示了未来三天可能出现的所有天气状态。每一天都可能是晴天，多云和雷雨三种天气状态中的一种，因此未来三天一共有3*3*3=27种可能的天气状态序列。

Pr(dry,damp,soggy | HMM) = Pr(dry,damp,soggy | sunny,sunny,sunny) + Pr(dry,damp,soggy | sunny,sunny ,cloudy) + Pr(dry,damp,soggy | sunny,sunny ,rainy) + . . . . Pr(dry,damp,soggy | rainy,rainy ,rainy)

经过计算预测观察状态所对应的隐藏状态为晴天，多云，雷雨
Read more: http://bluewhale.cc/2016-06-02/hidden-markov-model-1.html#ixzz72vUoEEqC

3，HMM解决的三个问题

定义HMM中用到的变量（2.1节适用）

3.1观测序列概率

（3.1.1）暴力解法

 （3.1.2）. 前向后向算法：

前向算法 :

先来解释一下HMM的向前算法：

　　前向后向算法是前向算法和后向算法的统称，这两个算法都可以用来求HMM观测序列的概率。我们先来看看前向算法是如何求解这个问题的。

　　前向算法本质上属于动态规划的算法，也就是我们要通过找到局部状态递推的公式，这样一步步的从子问题的最优解拓展到整个问题的最优解。在这里我们认为随机过程中各个状态St的概率分布，只与它的前一个状态St-1有关，同时任何时刻的观察状态只仅仅依赖于当前时刻的隐藏状态。

　　在t时刻我们定义观察状态的概率为：

　　　　　　　　　　　　　　　　αt(i)=P(o1,o2,...ot,it=qi|λ)

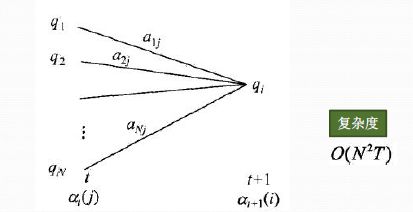
　　从下图可以看出，我们可以基于时刻t时各个隐藏状态的前向概率，再乘以对应的状态转移概率，即αt(j)aji就是在时刻t观测到o1,o2,...ot，即时刻t隐藏状态qj,qj总和再乘以该时刻的发射概率得到时刻t+1隐藏状态qi的概率。

　下面总结下前向算法。

　　　　输入：HMM模型λ=(A,B,Π)λ=(A,B,Π)，观测序列O=(o1,o2,...oT)

　　　　输出：观测序列概率P(O|λ)

　　　　1) 计算时刻1的各个隐藏状态前向概率：

　　　　　　α1(i)=πibi(o1),i=1,2,...N

　　　　2) 递推时刻2,3,...T时刻的前向概率：

　　　　　　

　　　　3) 计算最终结果：

　　　　　　

　　　　从递推公式可以看出，我们的算法时间复杂度是O(TN2)，比暴力解法的时间复杂度O(TNT)少了几个数量级。

实例说明：

3个盒子，每个盒子都有红、白两种球，具体情况如下：

　　　　盒子          1　　 2　　3

　　　　红球数      5　　4　　 7

　　　　黑球数      5　　6　　 3

　　　按照下面的方法从盒子里抽球，开始的时候，从第一个盒子抽球的概率是0.2，从第二个盒子抽球的概率是0.4，从第三个盒子抽球的概率是0.4。以这个概率抽一次球后，将球放回。然后从当前盒子转移到下一个盒子进行抽球。规则是：如果当前抽球的盒子是第一个盒子，则以0.5的概率仍然留在第一个盒子继续抽球，以0.2的概率去第二个盒子抽球，以0.3的概率去第三个盒子抽球。如果当前抽球的盒子是第二个盒子，则以0.5的概率仍然留在第二个盒子继续抽球，以0.3的概率去第一个盒子抽球，以0.2的概率去第三个盒子抽球。如果当前抽球的盒子是第三个盒子，则以0.5的概率仍然留在第三个盒子继续抽球，以0.2的概率去第一个盒子抽球，以0.3的概率去第二个盒子抽球。如此下去，直到重复三次，得到一个球的颜色的观测序列:

　　　　　　　　　　　　　　　　　　O={红，白，红}

　　注意在这个过程中，观察者只能看到球的颜色序列，却不能看到球是从哪个盒子里取出的。

如下图：

根据HMM的定义，我们可以得到观察集合：

　　　　　　　　　　　　V=｛红、白｝ M=2

隐藏的状态是：

　　　　　　　　Q=｛盒子1、盒子2、盒子3｝ N=3

而观察序列和状态序列的长度为3.

对应的矩阵表示为：

初始状态序列：

　　　　　　　　∏={0.2.0.4.0.4}T

状态转移矩阵：

　　　　　　   　|0.5　　0.2　　0.3|

　　　　　　A=  |0.3　　0.5　　0.2|

　　　　　　　   |0.2　　0.3　　0.5|

观察状态矩阵：

　　　　　　   　|0.5　　0.5|

　　　　　　B=  |0.4　　0.6|

　　　　　　　   |0.7　　0.3|

1、暴力求解：

 　　①红色球

　　　　　　隐藏状态是盒子1:α1(1)=π1b1(o1)=0.2×0.5=0.1

　　　　　　隐藏状态是盒子2:α1(2)=π2b2(o1)=0.4×0.4=0.16

　　　　　　隐藏状态是盒子3:α1(3)=π3b3(o1)=0.4×0.7=0.28

　　②第一次红色球前提下第二次白色球

　　　　　　　　隐藏状态是盒子1:α2(1)=[0.1∗0.5+0.16∗0.3+0.28∗0.2]×0.5=0.077

　　　　　　隐藏状态是盒子2:α2(2)=[0.1∗0.2+0.16∗0.5+0.28∗0.3]×0.6=0.1104

　　　　　　隐藏状态是盒子3:α2(3)=[0.1∗0.3+0.16∗0.2+0.28∗0.5]×0.3=0.0606

　　③第一次红色球、第二次白色球且第三次红色球

　　　　　　隐藏状态是盒子1:α3(1)=[0.077∗0.5+0.1104∗0.3+0.0606∗0.2]×0.5=0.04187

　　　　　　 隐藏状态是盒子2:α3(2)=[0.077∗0.2+0.1104∗0.5+0.0606∗0.3]×0.4=0.03551

　　　　　　隐藏状态是盒子3:α3(3)=[0.077∗0.3+0.1104∗0.2+0.0606∗0.5]×0.7=0.05284

最终我们求出观测序列:O={红，白，红}的概率为：

　　　　　　P=0.04187+0.03551+0.05284=0.13022

1、python代码实现：

# -*- coding: UTF-8 -*-
import numpy as np
def Forward(trainsition_probability,emission_probability,pi,obs_seq):
    """
    :param trainsition_probability:trainsition_probability是状态转移矩阵
    :param emission_probability: emission_probability是发射矩阵
    :param pi: pi是初始状态概率
    :param obs_seq: obs_seq是观察状态序列
    :return: 返回结果
    """
    trainsition_probability = np.array(trainsition_probability)
    emission_probability  = np.array(emission_probability)

    pi = np.array(pi)
    Row = np.array(trainsition_probability).shape[0]

    F = np.zeros((Row,Col))                      #最后要返回的就是F，就是我们公式中的alpha
    F[:,0] = pi * np.transpose(emission_probability[:,obs_seq[0]])  #这是初始化求第一列,就是初始的概率*各自的发射概率
    for t in range(1,len(obs_seq)):              #这里相当于填矩阵的元素值
        for n in range(Row):                     #n是代表隐藏状态的
            F[n,t] = np.dot(F[:,t-1],trainsition_probability[:,n])*emission_probability[n,obs_seq[t]]   #对应于公式,前面是对应相乘
    return F

if __name__ == '__main__':
    trainsition_probability = [[0.5,0.2,0.3],[0.3,0.5,0.2],[0.2,0.3,0.5]]
    emission_probability = [[0.5,0.5],[0.4,0.6],[0.7,0.3]]
    pi = [0.2,0.4,0.4]

    #然后下面先得到前向算法,在A,B,pi参数已知的前提下，求出特定观察序列的概率是多少?
    obs_seq = [0,1,0]
    Row = np.array(trainsition_probability).shape[0]
    Col = len(obs_seq)

    F = Forward(trainsition_probability,emission_probability,pi,obs_seq)
    print (F)

后向算法 ：

总结：

观测序列概率 Python 实现

本章使用 hmmlearn 库实现，文档、

import numpy as np
from hmmlearn import hmm

states = ["box 1", "box 2", "box3"]
n_states = len(states)

observations = ["red", "white"]
n_observations = len(observations)

start_probability = np.array([0.2, 0.4, 0.4])

transition_probability = np.array([
  [0.5, 0.2, 0.3],
  [0.3, 0.5, 0.2],
  [0.2, 0.3, 0.5]
])

emission_probability = np.array([
  [0.5, 0.5],
  [0.4, 0.6],
  [0.7, 0.3]
])

model = hmm.MultinomialHMM(n_components=n_states)
model.startprob_=start_probability
model.transmat_=transition_probability
model.emissionprob_=emission_probability

seen = np.array([[0,1,0]]).T
print model.score(seen)

注意：score函数返回的是以自然对数为底的对数概率值，因此会是负数

3.2HMM 参数学习

（3.2.1）. 鲍姆-韦尔奇算法原理

HMM 的参数学习一般采用 鲍姆-韦尔奇算法，其思想就是 EM算法

 

 （3.2.2）. 鲍姆-韦尔奇算法推导

arg max f(x): 当f(x)取最大值时，x的取值

arg min f(x)：当f(x)取最小值时，x的取值

HMM 参数学习 Python 实现：

import numpy as np
from hmmlearn import hmm

states = ["box 1", "box 2", "box3"]
n_states = len(states)

observations = ["red", "white"]
n_observations = len(observations)
model2 = hmm.MultinomialHMM(n_components=n_states, n_iter=20, tol=0.01)
X2 = np.array([[0],[1],[0],[1],[0],[0],[0],[1],[1],[0],[1],[1]])
model2.fit(X2,lengths=[4,4,4])
print model2.startprob_
print model2.transmat_
print model2.emissionprob_
print model2.score(X2)
model2.fit(X2)
print model2.startprob_
print model2.transmat_
print model2.emissionprob_
print model2.score(X2)
model2.fit(X2)
print model2.startprob_
print model2.transmat_
print model2.emissionprob_
print model2.score(X2)

3.3，HMM 解码问题

（3.31）. HMM 解码问题概述

HMM 的解码问题是给定模型，求给定观测序列条件下，最可能出现的对应的隐藏状态序列。

解码问题公式定义：

（3.3.2）. 维特比算法流程

 

 

 （3.3.3）HMM 解码 Python 实现

import numpy as np
from hmmlearn import hmm

states = ["box 1", "box 2", "box3"]
n_states = len(states)

observations = ["red", "white"]
n_observations = len(observations)

start_probability = np.array([0.2, 0.4, 0.4])

transition_probability = np.array([
  [0.5, 0.2, 0.3],
  [0.3, 0.5, 0.2],
  [0.2, 0.3, 0.5]
])

emission_probability = np.array([
  [0.5, 0.5],
  [0.4, 0.6],
  [0.7, 0.3]
])

model = hmm.MultinomialHMM(n_components=n_states)
model.startprob_=start_probability
model.transmat_=transition_probability
model.emissionprob_=emission_probability

seen = np.array([[0,1,0]]).T
print( model.score(seen))
seen = np.array([[0,1,0]]).T
logprob, box = model.decode(seen, algorithm="viterbi")
print("The ball picked:", ", ".join(map(lambda x: observations[x], seen)))
print("The hidden box", ", ".join(map(lambda x: states[x], box)))

总结 ：

参考视频：机器学习-白板推导系列(十四)-隐马尔可夫模型HMM（Hidden Markov Model）_哔哩哔哩_bilibili

参考文章：【归纳综述】马尔可夫、隐马尔可夫 HMM 、条件随机场 CRF 全解析及其python实现 - 知乎 (zhihu.com)

（三）马尔可夫随机场 MRF及命名实体识别

（1）什么叫随机场？

随机场是由若干个位置组成的整体，当给每一个位置中按照某种分布随机赋予一个值之后，其全体就叫做随机场。

例：假如我们有一个十个词形成的句子需要做词性标注。这十个词每个词的词性可以在我们已知的词性集合（名词，动词...)中去选择。当我们为每个词选择完词性后，这就形成了一个随机场。

马尔可夫随机场是随机场的一个具有马尔可夫性得特例，它假设随机场中某一个位置的赋值仅仅与和它相邻的位置的赋值有关，和与其不相邻的位置的赋值无关。

(2)命名实体识别入门案例

import numpy as np
# 第三方进度条库
from tqdm import tqdm


class HMM_Model:
    def __init__(self):
        # 标记-id
        self.tag2id = {'B-PER': 0,
                       'I-PER': 1,
                       'B-LOC': 2,
                       'I-LOC': 3,
                       'B-ORG': 4,
                       'I-ORG': 5,
                       'O': 6}
        # id-标记
        self.id2tag = dict(zip(self.tag2id.values(), self.tag2id.keys()))
        # 表示所有可能的标签个数N
        self.num_tag = len(self.tag2id)
        # 所有字符的Unicode编码个数 x16
        self.num_char = 65535
        # 转移概率矩阵,N*N
        self.A = np.zeros((self.num_tag, self.num_tag))
        # 发射概率矩阵,N*M
        self.B = np.zeros((self.num_tag, self.num_char))
        # 初始隐状态概率,N
        self.pi = np.zeros(self.num_tag)
        # 无穷小量
        self.epsilon = 1e-100

    def train(self, corpus_path):
        '''
        函数功能：通过数据训练得到A、B、pi
        :param corpus_path: 数据集文件路径
        :return: 无返回值
        '''
        with open(corpus_path, mode='r', encoding='utf-8') as f:
            # 读取训练数据
            lines = f.readlines()
        print('开始训练数据：')
        for i in tqdm(range(len(lines))):
            if len(lines[i]) == 1:
                # 空行，即只有一个换行符，跳过
                continue
            else:
                # split()的时候，多个空格当成一个空格
                cut_char, cut_tag = lines[i].split()
                # ord是python内置函数
                # ord(c)返回字符c对应的十进制整数
                self.B[self.tag2id[cut_tag]][ord(cut_char)] += 1
                if len(lines[i - 1]) == 1:
                    # 如果上一个数据是空格
                    # 即当前为一句话的开头
                    # 即初始状态
                    self.pi[self.tag2id[cut_tag]] += 1
                    continue
                pre_char, pre_tag = lines[i - 1].split()
                self.A[self.tag2id[pre_tag]][self.tag2id[cut_tag]] += 1
        # 为矩阵中所有是0的元素赋值为epsilon
        self.pi[self.pi == 0] = self.epsilon
        # 防止数据下溢,对数据进行对数归一化
        self.pi = np.log(self.pi) - np.log(np.sum(self.pi))
        self.A[self.A == 0] = self.epsilon
        # axis=1将每一行的元素相加，keepdims=True保持其二维性
        self.A = np.log(self.A) - np.log(np.sum(self.A, axis=1, keepdims=True))
        self.B[self.B == 0] = self.epsilon
        self.B = np.log(self.B) - np.log(np.sum(self.B, axis=1, keepdims=True))
        print('训练完毕！')

    def viterbi(self, Obs):
        '''
        函数功能：使用viterbi算法进行解码
        :param Obs: 要解码的文本字符串
        :return: 最可能的隐状态路径
        '''
        # 获得观测序列的文本长度
        T = len(Obs)
        # T*N
        delta = np.zeros((T, self.num_tag))
        # T*N
        psi = np.zeros((T, self.num_tag))
        # ord是python内置函数
        # ord(c)返回字符c对应的十进制整数
        # 初始化
        delta[0] = self.pi[:] + self.B[:, ord(Obs[0])]
        # range（）左闭右开
        for i in range(1, T):
            # arr.reshape(4,-1) 将arr变成4行的格式，列数自动计算的(c=4, d=16/4=4)
            temp = delta[i - 1].reshape(self.num_tag, -1) + self.A
            # 按列取最大值
            delta[i] = np.max(temp, axis=0)
            # 得到delta值
            delta[i] = delta[i, :] + self.B[:, ord(Obs[i])]
            # 取出元素最大值对应的索引
            psi[i] = np.argmax(temp, axis=0)
        # 最优路径回溯
        path = np.zeros(T)
        path[T - 1] = np.argmax(delta[T - 1])
        for i in range(T - 2, -1, -1):
            path[i] = int(psi[i + 1][int(path[i + 1])])
        return path

    def predict(self, Obs):
        '''
        函数功能：对文本进行命名实体识别
        :param Obs: 要识别的文本
        :return: 无返回
        '''
        T = len(Obs)
        path = self.viterbi(Obs)
        for i in range(T):
            print(Obs[i] + self.id2tag[path[i]] + '_|', end='')


def main():
    model = HMM_Model()
    model.train('./BIO_train.txt')
    # 识别人名、地名、组织机构名
    s = '刘晓明，国籍中国，目前任职于中央广播电视台'
    model.predict(s)


if __name__ == '__main__':
    main()

结果： 

例：如果我们假设所有词的词性只和它相邻的词的词性有关时，这个随机场就特化成一个马尔科夫随机场。比如第三个词的词性除了与自己本身的位置有关外，只与第二个词和第四个词的词性有关。

我们知道隐马尔可夫模型的三要素是A(状态转移概率矩阵)、B(观测概率矩阵)、Pi(初始状态概率向量)，本例采用监督学习方法来估计这三个参数的值，用于监督学习的BIO标注数据集，参考资料[1]，最后通过Viterbi算法进行预测。从输出结果来看，效果还是不错的，当然本例基于HMM的命名实体识别效果其实并不是特别的好，这与训练数据以及算法本身的局限性等有关。但我认为本例可以作为NER新手的一个入门案例，或者说是一个很好的Demo。

我们看下面这个图：

这是电子病历的命名实体识别流程，结合本例，或许能够更好的了解该如何来做命名实体识别。那么，我们再来梳理一下基于HMM模型进行命名实体识别的流程：先得到一份文本，然后对文本进行标注，本例采用BIO标注法，对于标注数据，我们还需要按照一定规则进行打断，比如句号，对于中文序列，通过ord（）函数与整数值建立唯一对应，对于标签数据，采用整数值id对的方式建立对应关系，然后将标注数据集输入到训练模型，从而学习到模型参数，基于模型参数本例采用Vterbi算法进行解码预测，将预测结果输出便得到了命名实体识别结果。

本内容如有不到之处，欢迎批评指正。

参考资料：

[1]https://gitee.com/moon_mx/HMM_NER

[2]杨飞洪,张宇,覃露,李姣.中文电子病历的命名实体识别研究进展[J].中国数字医学,2020,15(02):9-12.