Common Spatial Pattern(CSP)共空间模式(包含Matlab代码)
文章目录
- 前言
- 1.CSP算法
- 2.代码实现
-
- 2.1-learnCSPLagrangian.m
- 2.2-learnCSP.m
- 2.3-extractCSPFeatures.m
- 2.4-Test.m
- 2.5-filterFun.m
- 2.6-运行结果
- 3.补充
前言
共空间模式(Common Spatial Pattern, CSP)作为运动想象脑机接口的常用特征提取算法,相信很多接触过运动想象领域的人都大概知道该算法,CSP的原理以及推导下面这篇博客做出了详细说明(也就是像在CSSP[1]那种定义的方法):
点此跳转
但是,在RCSP论文[2]中作者为了给CSP统一的公理化定义给出了不同于上面博客的定义形式,在RCSP后,许多论文也随着RCSP的思路来定义CSP公式,因此也有必要了解一下这种定义,以下为RCSP中对CSP算法的描述的翻译。
(传统的CSP方法是通过特征向量和白化矩阵构造空域滤波器 ω ω ω, 而RCSP中则是将 ω ω ω的构造问题转化为最优化问题)
(PS:第一次翻译,仅供参考… )
1.CSP算法
CSP的目标是学习空间滤波器,使得同一类带通滤波后的脑电信号方差最大化,同时使得其与另一类的方差最小。因为给定频带滤波后的脑电信号的方差对应于该频带内的信号功率,CSP旨在实现基于频带功率特征的最优BCI识别。形式上,CSP使用空间滤波器ω极化以下(目标)函数:

其中, T T T表示矩阵的转置, X i X_{i} Xi 是类 i i i 的数据矩阵( X X X的行是训练样本,列为通道), C i C_{i} Ci 为类 i i i 的空间协方差矩阵,假定EEG信号的均值为0(当EEG信号进行带通滤波时,通常会满足这一假设)。 这个优化问题是可以被解决的(虽然方法不唯一), 首先注意到, J ( ω ) J(ω) J(ω) 函数是保持不变的如果滤波器 w w w 被缩放。 事实上, J ( k ω ) = J ( ω ) J(kω)=J(ω) J(kω)=J(ω), k k k是一个实常数,这意味着 ω ω ω 的缩放是任意的。因此,对 J ( ω ) J(ω) J(ω)求极值等同于对 ω T C 1 w \omega^{T}{C}_{1}w ωTC1w 求极值,且限制条件为 ω T C 2 w = 1 \omega^{T}{C}_{2}w=1 ωTC2w=1 因为总可能找到 ω ω ω 的缩放,使 ω T C 2 w = 1 \omega^{T}{C}_{2}w=1 ωTC2w=1 。
通过拉格朗日数乘法,这个带约束的最优化问题等于极化以下函数:
滤波器 ω 对 L L L 求极值使得 L L L 对 ω 的导数等于 0 0 0:
于是我们得到标准的特征值问题。 空间滤波器最优化( 公式(1) )的特征向量为 M = C 2 − 1 C 1 M={C}_{2}^{-1}C_{1} M=C2−1C1
分别对应其最大以及最小的特征值。 当使用CSP时,提取的特征是EEG信号方差投影到滤波器 ω ω ω上后的对数。
2.代码实现
2.1-learnCSPLagrangian.m
这里的learnCSPLagrangian.m即对应上文中的目标函数CSP构造法
function CSPMatrix = learnCSPLagrangian(EEGSignals)
%by Fabien
%created: 02/03/2010
%last revised: 02/03/2010
%输入
%EEGSignals: 需要训练的EEG信号,包括2类,其结构如下:
% EEGSignals.x: EEG信号为[Ns*Nc*Nt]的三维矩阵形式,其中
% Ns:每个trial的EEG样本数量
% Nc:通道数量(EEG电极)
% Nt: trials 的数量
% EEGSignals.y: 一个[1*Nt]的向量包括每一类的类标签
% EEGSignals.s: 采样率
%输出
%CSPMatrix: 一个学习到的CSP滤波器(一个[通道数量 * 通道数量] 的矩阵,用该矩阵的行作为滤波)
%初始化以及合法性检查
nbChannels = size(EEGSignals.x,2); %通道大小
nbTrials = size(EEGSignals.x,3); %trials大小
classLabels = unique(EEGSignals.y); %获得类标签
nbClasses = length(classLabels); %获取分类数
if nbClasses ~= 2 %分类数大于2,报错!
disp('ERROR! CSP can only be used for two classes');
return;
end
covMatrices = cell(nbClasses,1); %每一类的协方差矩阵
%计算每个trial标准化后的协方差矩阵
trialCov = zeros(nbChannels,nbChannels,nbTrials);
for t=1:nbTrials
E = EEGSignals.x(:,:,t)';
EE = E * E';
trialCov(:,:,t) = EE ./ trace(EE);
end
clear E;
clear EE;
%计算每一类的协方差矩阵
for c=1:nbClasses
covMatrices{c} = mean(trialCov(:,:,EEGSignals.y == classLabels(c)),3);
covMatrices{c} = covMatrices{c} ./ sum(EEGSignals.y == classLabels(c));
end
%计算需要分解的矩阵M
M = inv(covMatrices{2}) * covMatrices{1};
%矩阵M的特征值分解
[U D] = eig(M);
eigenvalues = diag(D);
[eigenvalues egIndex] = sort(eigenvalues, 'descend');
U = U(:,egIndex);
CSPMatrix = U';
2.2-learnCSP.m
这里的learnCSP.m 即是用传统方式构造的滤波器 w w w,即通过特征向量以及白化矩阵形式,可以从代码的观点比较两种不同的构造算法。
function CSPMatrix = learnCSP(EEGSignals)
%by Fabien LOTTE
%created: 02/03/2010
%last revised: 02/03/2010
%输入
%EEGSignals: 需要训练的EEG信号,包括2类,其结构如下:
% EEGSignals.x: EEG信号为[Ns*Nc*Nt]的三维矩阵形式,其中
% Ns:每个trial的EEG样本数量
% Nc:通道数量(EEG电极)
% Nt: trials 的数量
% EEGSignals.y: 一个[1*Nt]的向量包括每一类的类标签
% EEGSignals.s: 采样率
%输出
%CSPMatrix: 一个学习到的CSP滤波器(一个[通道数量 * 通道数量] 的矩阵,用该矩阵的行作为滤波)
%初始化以及合法性检查
nbChannels = size(EEGSignals.x,2); %通道大小
nbTrials = size(EEGSignals.x,3); %trials大小
classLabels = unique(EEGSignals.y); %获得类标签
nbClasses = length(classLabels); %获取分类数
if nbClasses ~= 2 %分类数大于2,报错!
disp('ERROR! CSP can only be used for two classes');
return;
end
covMatrices = cell(nbClasses,1); %每一类的协方差矩阵
%计算每个trial标准化后的协方差矩阵
trialCov = zeros(nbChannels,nbChannels,nbTrials);
for t=1:nbTrials
E = EEGSignals.x(:,:,t)';
EE = E * E';
trialCov(:,:,t) = EE ./ trace(EE);
end
clear E;
clear EE;
%%%%%%%%%%%%%%%%%%%%%%这里开始不同了%%%%%%%%%%%%%%%%%%%%%
%计算每一类的协方差矩阵
for c=1:nbClasses
covMatrices{c} = mean(trialCov(:,:,EEGSignals.y == classLabels(c)),3);
end
%总的协方差矩阵
covTotal = covMatrices{1} + covMatrices{2};
%总协方差矩阵的白化转换
[Ut Dt] = eig(covTotal); %注意:特征值初始是升序排列的
eigenvalues = diag(Dt);
[eigenvalues egIndex] = sort(eigenvalues, 'descend');
Ut = Ut(:,egIndex);
P = diag(sqrt(1./eigenvalues)) * Ut';
%通过P进行第一类协方差矩阵的转换
transformedCov1 = P * covMatrices{1} * P';
%协方差矩阵的EVD
[U1 D1] = eig(transformedCov1);
eigenvalues = diag(D1);
[eigenvalues egIndex] = sort(eigenvalues, 'descend');
U1 = U1(:, egIndex);
CSPMatrix = U1' * P;
2.3-extractCSPFeatures.m
extractCSPFeatures.m用于提取CSP特征,其中的CSPMatrix投影矩阵输入参数通过2.1或2.2中的某一种方法获得。
function features = extractCSPFeatures(EEGSignals, CSPMatrix, nbFilterPairs)
%Copyright (C) 2010 Fabien LOTTE
%输入
%EEGSignals: 需要训练的EEG信号,包括2类,其结构如下:
% EEGSignals.x: EEG信号为[Ns*Nc*Nt]的三维矩阵形式,其中
% Ns:每个trial的EEG样本数量
% Nc:通道数量(EEG电极)
% Nt: trials 的数量
% EEGSignals.y: 一个[1*Nt]的向量包括每一类的类标签
% EEGSignals.s: 采样率
%CSPMatrix: 学习到的CSP投影矩阵
%nbFilterPairs: CSP-m参数
%输出
%features: 从EEG数据集特征出来的特征, 是一个[Nt *(2*nbFilterPairs+1)]的矩阵,
% 最后一列为类标签
%初始化
nbTrials = size(EEGSignals.x,3); %trial大小
features = zeros(nbTrials, 2*nbFilterPairs); %声明特征
Filter = CSPMatrix([1:nbFilterPairs (end-nbFilterPairs+1):end],:); %根据CSP-m参数确定滤波器大小
for t=1:nbTrials
%投影数据到CSP滤波器
projectedTrial = Filter * EEGSignals.x(:,:,t)';
%投影信号的对数方差作为生成特征
variances = var(projectedTrial,0,2);
for f=1:length(variances)
features(t,f) = log(variances(f));
end
% features(t,end) = EEGSignals.y(t); %不要拼接标签
end
2.4-Test.m
Test.m 用于测试。 其中,用到的数据集为BCIcomp2002.mat(到我的博客资源可以下载),这里不在过多描述数据集了,分类器用libsvm。
load BCIcomp2002.mat
%% 先对EEG进行带通滤波
initParam.low=8; %高通滤波参数设置
initParam.high=30; %低通滤波参数设置
initParam.sampleRate=128; %采样率
initParam.filterorder = 4; %butterworth滤波器阶数
m=2;
for i=1:size(x_train,3)
tmp_train(:,:,i)=filterFun(x_train(:,:,i),initParam);
tmp_test(:,:,i)=filterFun(x_test(:,:,i),initParam);
end
x_train=tmp_train(128*3:end,:,:); %MI 3-9
x_test=tmp_test(128*3:end,:,:);
%% 将数据格式变为符合函数输入的形式
EEG.x=x_train; %训练集
EEG.y=y_train; %训练集标签
EEG.s=128; %采样率Hz
EEG_Test.x=x_test; %测试集
EEG_Test.y=y_test;
EEG_Test.s=128;
%% 计算CSP投影矩阵
W=learnCSPLagrangian(EEG); %目标函数法特征W
% W=learnCSP(EEG); %传统白化法W
%% 提取CSP特征
feature_train=extractCSPFeatures(EEG,W,m); %提取训练集特征
feature_test=extractCSPFeatures(EEG_Test,W,m); %提取测试集特征
%% 分类
model=svmtrain(y_train,feature_train,'-c 2 -g 0.1250'); %训练模型
predict_label=svmpredict(y_test,feature_test,model);
2.5-filterFun.m
%% 对运动想象数据进行滤波
%输入:data 待滤波EEG数据
% initParam.low 高通滤波参数设置
% initParam.high 低通滤波参数设置
% initParam.sampleRate 采样率
% initParam.filterorder butterworth滤波器阶数
%返回:filterdata 滤波后EEG数据
function filterdata=filterFun(data,initParam)
%% 设置滤波参数
% filtercutoff = [low/(Fs/2) high/(Fs/2)];
filtercutoff = [initParam.low*2/initParam.sampleRate initParam.high*2/initParam.sampleRate];
[filterParamB, filterParamA] = butter(initParam.filterorder,filtercutoff);
filterdata= filter( filterParamB, filterParamA, data);
2.6-运行结果
无论是目标函数法提取出来的空间滤波器 w w w ,还是传统方法提取出来的 w w w 两者的分类准确率都一样。

下面再来看看两种方法提取出来的具体空间滤波器 w w w数值, learnCSPLagrangian.m(目标函数构造法)提取出来的 w w w如下:
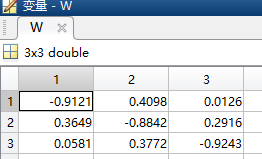
learnCSP.m(传统方法构造)提取出来的 w w w如下:
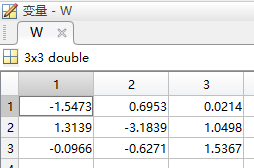
虽然分类准确率一样,但两种不同方法构造出来的空间滤波器数值上还有所区别的。
3.补充
即对 w T w^{T} wT求导等于 2 w T 2w^{T} 2wT 。
参考文献:
[1] Lemm S , Blankertz B , Curio G , et al. Spatio-spectral filters for improving the classification of single trial EEG.[J]. IEEE transactions on bio-medical engineering, 2005, 52(9):1541-8.
[2] Lotte F , Guan C . Regularizing Common Spatial Patterns to Improve BCI Designs: Unified Theory and New Algorithms[J]. IEEE Trans Biomed Eng, 2011, 58(2):355-362.
download: 点这里下载原文


