[目标检测]-涨点trick之ASFF:Learning Spatial Fusion for Single-Shot Object Detection笔记
1.综述
文章地址与文章代码;
文章主要思想可以简单的概括为fpn+attention;
文章的核心工作有两个
-
1.在yolov3的基础上采用了一系列更强的trick,获得了一个基于yolov3的超强baseline
主要包括如下技巧,详情可以参见论文
1) Guided Anchoring-一种anchor free 方法
2) Bag of Tricks-主要包括
mixup algorithm , cosine learning rate schedule, synchronized batch nor-malization technique.
详情论文里面有参考文献,请查阅
3) Additional IoU Loss -
2.提出了ASFF算法,实现了自适应的FPN结构下不同level层的特征融合,提升了性能
总体来说比yolov3提升了6个点之多
对于基于FPN的单级检测器来说,不同特征尺度之间的不一致是其主要限制。因此提出了自适应空间特征融合(ASFF)。它学习了在空间上过滤冲突信息以抑制梯度反传的时候不一致的方法,从而改善了特征的比例不变性,并且推理开销降低。
2.自适应特征融合(ASFF)
为了更加充分的利用高层特征的语义信息和底层特征的细粒度特征,很多网络都会采用FPN的方式输出多层特征,但是无论是类似于YOLOv3还是RetinaNet,它们都多用element-wise sum 和 concatenation这种直接衔接或者相加的方式,论文认为这样并不能充分的利用不同尺度的特征,所以提出了Adaptively Spatial Feature Fusion(自适应特征融合方式)。
其结构如下
![[目标检测]-涨点trick之ASFF:Learning Spatial Fusion for Single-Shot Object Detection笔记_第1张图片](http://img.e-com-net.com/image/info8/0394558fc59f44e4b8e386b4a6cb67a7.jpg)
以上图为例,上图展示的为level3这个层级的特征融合,主要分为两步
- 1.按照变换规则将level1与level2的特征图变换为与level3尺寸,通道(H,W,C)相同的特征图
- 2.按照各自的权重系数进行相乘并进行求和,即可得到融合后的特征ASFF-3
(H,W,C)变换规则
对于需要上采样的层,如想得到ASFF3,需要将level1的特征图调整到和level3的特征图尺寸一致,采用的方式是先通过1*1卷积调整到和level3通道数一致,再用插值的方式将尺寸调整到一致。
而对于需要下采样的层,比如想得到ASFF1,对于level2的特征图到level1的特征图只需要用一个3*3并且步长为2的卷积就OK了,如果是level3的特征图到level1的特征图则需要在3*3且步长为2的卷积的基础上再加上一个步长为2的最大池化层。
完成不同level的特征图的(H,W,C)统一;
权重系数
对于权重参数α,β,γ,则是通过resize后的level1~level3特征图经过concat然后进行1*1卷积获得的。并且参数α,β,γ经过concat之后通过softmax使得它们的范围都在[0,1]并且和为1.这些权重系数都是在训练中通过反向传播获得到的。
![[目标检测]-涨点trick之ASFF:Learning Spatial Fusion for Single-Shot Object Detection笔记_第2张图片](http://img.e-com-net.com/image/info8/b9649e7c1c70443886f45c3e5e1c5c1a.jpg)
以ASFF-3的权重生成为例,作者将Level1_resized、Level2_resized、Level3(均为128×H×W),分别进行1×1卷积通道降维到16×H×W,然后三张特征图拼接成48×H×W的通道数,再进行1×1卷积降维到3×H×W,最后在进行softmax则得到了三个系数.
3.ASFF的原理
论文以YOLOv3为例,加入FPN后通过链式法则我们可以知道在反向传播的时候梯度计算如公式(3)所示:
![[目标检测]-涨点trick之ASFF:Learning Spatial Fusion for Single-Shot Object Detection笔记_第3张图片](http://img.e-com-net.com/image/info8/6b73e740ba08438bb57f20ba0f0e1b56.jpg)
稍微解释一下,左边的第一项 ∂ L ∂ x i j 1 \frac{\partial \mathcal{L}}{\partial \mathbf{x}_{i j}^{1}} ∂xij1∂L代表的是损失函数对level1的特征图的某个像素求导,在YOLOV3中不同尺度的层之间的尺度变化一般就是下采样和上采样,因此我们可以假设 ∂ x i j 1 → l ∂ x i j 1 ≈ 1 \frac{\partial \mathbf{x}_{i j}^{1 \rightarrow l}}{\partial \mathbf{x}_{i j}^{1}} \approx 1 ∂xij1∂xij1→l≈1,那么公式(3)可以简化为公式(4):
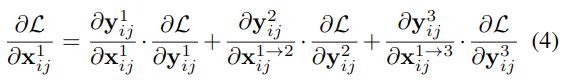
YOLOv3 和 其他的基于FPN的检测器(按元素求和concatenation),相当于对输出特征的activation操作,我们就可以认为 ∂ y i j 1 ∂ x i j 1 = 1 \frac{\partial \mathbf{y}_{i j}^{1}}{\partial \mathbf{x}_{i j}^{1}}=1 ∂xij1∂yij1=1和 ∂ y i j l ∂ x i j 1 → l = 1 \frac{\partial \mathbf{y}_{i j}^{l}}{\partial \mathbf{x}_{i j}^{1 \rightarrow l}}=1 ∂xij1→l∂yijl=1,于是有:
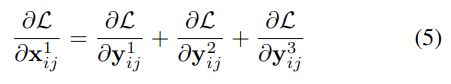
假设level1(i,j)对应特征图位置刚好有物体并且为正样本,那其他level上对应的(i,j)位置上就可能刚好为负样本,这样反向传播的梯度中既包含了正样本又包含了负样本,这种不连续性会对梯度结果造成干扰,并且降低训练的效率。而通过ASFF的方式,反向传播的梯度表达式就变成了(6):

因此,如果出现刚才的情况我们可以通过将 α 2 \alpha^{2} α2和 α 3 \alpha^{3} α3设置为0来解决,因为这样负样本的梯度不会结果造成干扰。
同时这也解释了为什么特征融合的权重参数来源于输出特征+卷积,因为融合的权重参数和特征是息息相关的。
4.可视化
视化的结果进一步解释了ASFF的有效性。比如对于斑马的检测,可以看到斑马实际上是在level1这个特征图上被检测到的(响应越大,heatmap越红),并且观察level1这一层的[公式],[公式],[公式]的权重可以发现,对于图中斑马这种大目标更容易被高层的特征捕捉到,因为对于大物体我们需要更大的感受野和高级语义特征。而对于下面的羊群的检测来讲,可以看到羊更多的是被level2和level3检测到,这也说明了对于小物体,我们更需要底层特征中的细粒度特征来辨别。
5.参考代码
class ASFF(nn.Module):
def __init__(self, level, rfb=False, vis=False):
super(ASFF, self).__init__()
self.level = level
# 输入的三个特征层的channels, 根据实际修改
self.dim = [512, 256, 256]
self.inter_dim = self.dim[self.level]
# 每个层级三者输出通道数需要一致
if level==0:
self.stride_level_1 = add_conv(self.dim[1], self.inter_dim, 3, 2)
self.stride_level_2 = add_conv(self.dim[2], self.inter_dim, 3, 2)
self.expand = add_conv(self.inter_dim, 1024, 3, 1)
elif level==1:
self.compress_level_0 = add_conv(self.dim[0], self.inter_dim, 1, 1)
self.stride_level_2 = add_conv(self.dim[2], self.inter_dim, 3, 2)
self.expand = add_conv(self.inter_dim, 512, 3, 1)
elif level==2:
self.compress_level_0 = add_conv(self.dim[0], self.inter_dim, 1, 1)
if self.dim[1] != self.dim[2]:
self.compress_level_1 = add_conv(self.dim[1], self.inter_dim, 1, 1)
self.expand = add_conv(self.inter_dim, 256, 3, 1)
compress_c = 8 if rfb else 16 #when adding rfb, we use half number of channels to save memory
self.weight_level_0 = add_conv(self.inter_dim, compress_c, 1, 1)
self.weight_level_1 = add_conv(self.inter_dim, compress_c, 1, 1)
self.weight_level_2 = add_conv(self.inter_dim, compress_c, 1, 1)
self.weight_levels = nn.Conv2d(compress_c*3, 3, kernel_size=1, stride=1, padding=0)
self.vis= vis
# 尺度大小 level_0 < level_1 < level_2
def forward(self, x_level_0, x_level_1, x_level_2):
if self.level==0:
level_0_resized = x_level_0
level_1_resized = self.stride_level_1(x_level_1)
level_2_downsampled_inter =F.max_pool2d(x_level_2, 3, stride=2, padding=1)
level_2_resized = self.stride_level_2(level_2_downsampled_inter)
elif self.level==1:
level_0_compressed = self.compress_level_0(x_level_0)
level_0_resized =F.interpolate(level_0_compressed, scale_factor=2, mode='nearest')
level_1_resized =x_level_1
level_2_resized =self.stride_level_2(x_level_2)
elif self.level==2:
level_0_compressed = self.compress_level_0(x_level_0)
level_0_resized =F.interpolate(level_0_compressed, scale_factor=4, mode='nearest')
if self.dim[1] != self.dim[2]:
level_1_compressed = self.compress_level_1(x_level_1)
level_1_resized = F.interpolate(level_1_compressed, scale_factor=2, mode='nearest')
else:
level_1_resized =F.interpolate(x_level_1, scale_factor=2, mode='nearest')
level_2_resized =x_level_2
level_0_weight_v = self.weight_level_0(level_0_resized)
level_1_weight_v = self.weight_level_1(level_1_resized)
level_2_weight_v = self.weight_level_2(level_2_resized)
levels_weight_v = torch.cat((level_0_weight_v, level_1_weight_v, level_2_weight_v),1)
levels_weight = self.weight_levels(levels_weight_v)
levels_weight = F.softmax(levels_weight, dim=1) # alpha等产生
fused_out_reduced = level_0_resized * levels_weight[:,0:1,:,:]+\
level_1_resized * levels_weight[:,1:2,:,:]+\
level_2_resized * levels_weight[:,2:,:,:]
out = self.expand(fused_out_reduced)
if self.vis:
return out, levels_weight, fused_out_reduced.sum(dim=1)
else:
return out
6.参考文章
1.ASFF使用小记
2.ASFF权重系数代码理解
3.ASFF全文梳理