数据分析-数据集划分-交叉验证
目录
交叉验证
k折交叉验证(k-fold cross validation)
分层k折交叉验证(stratified cross validation)
Sklearn的实现
k折交叉分类器
分层k折交叉分类器
打乱数据集后再划分
模型验证
交叉验证预测
学习曲线
交叉验证
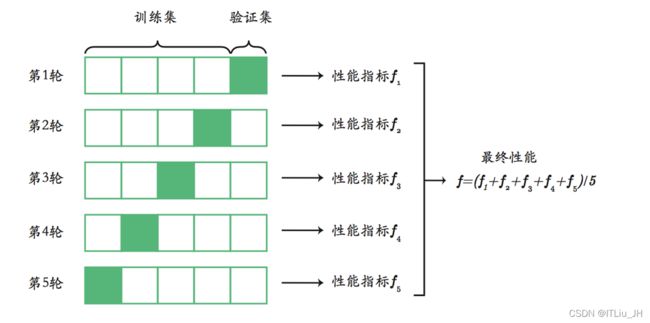
k折交叉验证(k-fold cross validation)
如果数据集按类别集中分布,某一类集中在一起,则标准交叉验证中的某一折,可能全部为一个类别,这一折外又很少或没有该类样本,如果这一折为验证集,那么在训练集中就没有或很少此类样本,模型训练的结果就会很差,在样本不均衡时表现尤为突出。
如 90% 的样本属于类别A只有 10% 的样本属于类别 B,k折交叉验证就容易导致以上问题出现。
分层k折交叉验证(stratified cross validation)
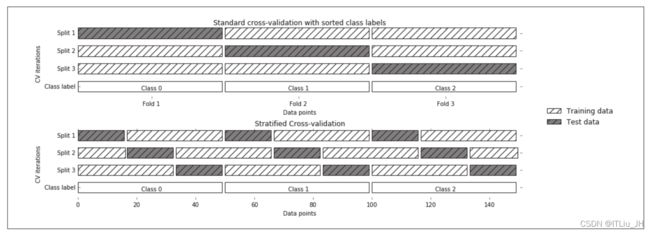
分层k折交叉验证使每个折内类别之间的比例与整个数据集中的类别比例相同。当数据按类别标签排序时,标准交叉验证与分层交叉验证的对比图如下(极端情况,3个类别,类别均衡):
可以看到标准交叉验证,3折时,每折对应一个类别,无论如何划分测试集和训练集,每次都有一个类别不在训练集中,不被模型学习到。
而采用分层k折交叉验证可保证每次的训练集中都包含所有的类别,测试集也一样。
将数据充分打乱后再采用K折交叉验证,也可以达到类似的效果。
Sklearn的实现
k折交叉分类器
model_selection.KFold
对数据集(X,y)4折划分。
from sklearn.model_selection import KFold
kf = KFold(n_splits=4)
kf.split(X,y)
分层k折交叉分类器
model_selection.StratifiedKFold
对数据集(X,y)分层3折划分。
from sklearn.model_selection import StratifiedKFold
skf = StratifiedKFold(n_splits=3)
skf.split(X,y)
打乱数据集后再划分
model_selection.ShuffleSplit
对数据集(X,y)乱序后10折划分。
from sklearn.model_selection import ShuffleSplit
shs=ShuffleSplit(n_splits=10) #打乱顺序后划分
shs.split(X,y)
模型验证
model_selection.cross_val_score 根据交叉验证计算模型分数
5折划分
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
print(cross_val_score(LogisticRegression(),X,y,cv=5)) #cv为数字5,5折交叉验证,输出5种分割的score。
[0.83236994 0.94508671 0.92774566 0.69855072 0.88695652]
使用shs划分
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
print(cross_val_score(LogisticRegression(),X,y,cv=shs)) #cv=shs,使用shs的划分,输出该分割的得分(10种)。[0.95953757 0.93641618 0.97109827 0.93063584 0.97109827 0.95375723 0.94797688 0.93641618 0.95953757 0.95953757]
使用skf划分
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
print(cross_val_score(LogisticRegression(),X,y,cv=skf)) #cv=skf,使用skf的划分,输出该分割的得分(3种)。[0.74131944 0.765625 0.86111111]
使用kf划分
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
print(cross_val_score(LogisticRegression(),X,y,cv=kf)) #cv=kf,使用kf的划分,输出该分割的得分(4种)。[0.78935185 0.88194444 0.91203704 0.85648148]
交叉验证预测
model_selection.cross_val_predict
from sklearn.model_selection import cross_val_predict
lr= LogisticRegression()
cross_val_predict(lr,X1,y1)学习曲线
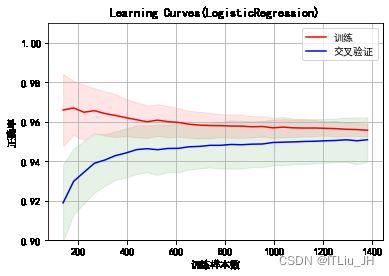
model_selection.learning_curve 学习曲线
from sklearn.model_selection import learning_curve
lr= LogisticRegression()
ss = ShuffleSplit(n_splits=10, test_size=0.2, random_state=0)
plt.title("Learning Curves(LogisticRegression)")
plt.ylim([0.90,1.01])
plt.xlabel("训练样本数")
plt.ylabel("正确率")
train_sizes, train_scores, test_scores = learning_curve(
lr, X1, y1, cv=ss,train_sizes=np.linspace(.1, 1.0,30))
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
plt.grid()
plt.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体,解决中文显示问题
plt.rcParams['axes.unicode_minus'] = False # 解决'-'显示为方块的问题
plt.fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha=0.1,
color="r")
plt.fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1, color="g")
plt.plot(train_sizes, train_scores_mean, color="r",
label="训练")
plt.plot(train_sizes, test_scores_mean, color="b",
label="交叉验证")
plt.legend(loc="best")