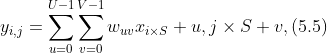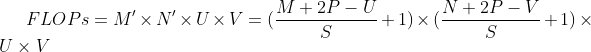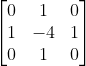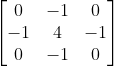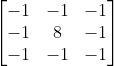神经网络与深度学习（六）卷积神经网络（1）卷积
目录
5.1 卷积
5.1.1 二维卷积运算
5.1.2 二维卷积算子
5.1.3 二维卷积的参数量和计算量
5.1.4 感受野
5.1.5 卷积的变种
5.1.5.1 步长（Stride）
5.1.5.2 零填充（Zero Padding）
5.1.6 带步长和零填充的二维卷积算子
5.1.7 使用卷积运算完成图像边缘检测任务
边缘检测系列1：传统边缘检测算子
引入
算法原理
代码实现
构建通用的边缘检测算子
图像边缘检测测试函数
Roberts 算子
Prewitt 算子
Sobel 算子
Scharr 算子
Krisch 算子
Robinson算子 编辑
Laplacian 算子
边缘检测系列2：简易的 Canny 边缘检测器
引入
算法原理
代码实现
基于 OpenCV 实现快速的 Canny 边缘检测
基于 Numpy 模块实现简单的 Canny 检测器
基于 Pytorch 实现的 Canny 边缘检测器
边缘检测系列3：【HED】 Holistically-Nested 边缘检测
边缘检测系列4：【RCF】基于更丰富的卷积特征的边缘检测
边缘检测系列5：【CED】添加了反向细化路径的 HED 模型
参考资料
卷积神经网络（Convolutional Neural Network，CNN）
- 受生物学上感受野机制的启发而提出。
- 一般是由卷积层、汇聚层和全连接层交叉堆叠而成的前馈神经网络。
- 有三个结构上的特性：局部连接、权重共享、汇聚。
- 具有一定程度上的平移、缩放和旋转不变性。
- 和前馈神经网络相比，卷积神经网络的参数更少。
- 主要应用在图像和视频分析的任务上，其准确率一般也远远超出了其他的神经网络模型。
- 近年来卷积神经网络也广泛地应用到自然语言处理、推荐系统等领域。
5.1 卷积
考虑到使用全连接前馈网络来处理图像时，会出现如下问题：
（1）模型参数过多，容易发生过拟合。 在全连接前馈网络中，隐藏层的每个神经元都要跟该层所有输入的神经元相连接。随着隐藏层神经元数量的增多，参数的规模也会急剧增加，导致整个神经网络的训练效率非常低，也很容易发生过拟合。
（2）难以提取图像中的局部不变性特征。 自然图像中的物体都具有局部不变性特征，比如尺度缩放、平移、旋转等操作不影响其语义信息。而全连接前馈网络很难提取这些局部不变性特征。
卷积神经网络有三个结构上的特性：局部连接、权重共享和汇聚。这些特性使得卷积神经网络具有一定程度上的平移、缩放和旋转不变性。和前馈神经网络相比，卷积神经网络的参数也更少。因此，通常会使用卷积神经网络来处理图像信息。
卷积是分析数学中的一种重要运算，常用于信号处理或图像处理任务。本节以二维卷积为例来进行实践。
5.1.1 二维卷积运算
在机器学习和图像处理领域，卷积的主要功能是在一个图像（或特征图）上滑动一个卷积核，通过卷积操作得到一组新的特征。在计算卷积的过程中，需要进行卷积核的翻转，而这也会带来一些不必要的操作和开销。因此，在具体实现上，一般会以数学中的互相关运算来代替卷积。
在神经网络中，卷积运算的主要作用是抽取特征，卷积核是否进行翻转并不会影响其特征抽取的能力。特别是当卷积核是可学习的参数时，卷积和互相关在能力上是等价的。因此很多时候，为方便起见，会直接用互相关来代替卷积。
对于一个输入矩阵
和一个滤波器
，它们的卷积为：
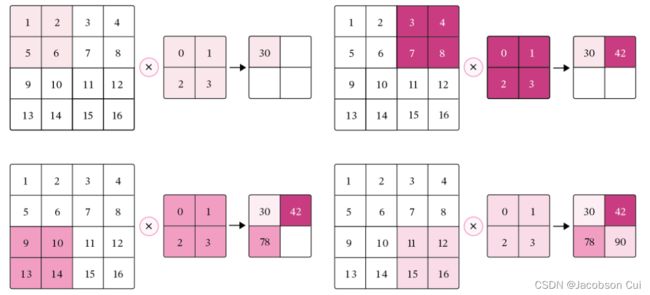
下图给出了卷积计算的示例。
经过卷积运算后，最终输出矩阵大小则为
M′=M−U+1,（5.2）
N′=N−V+1.（5.3）
可以发现，使用卷积处理图像，会有以下两个特性：
- 在卷积层(假设是第
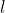层)中的每一个神经元都只和前一层(第
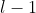层)中某个局部窗口内的神经元相连，构成一个局部连接网络，这也就是卷积神经网络的局部连接特性。 - 由于卷积的主要功能是在一个图像（或特征图）上滑动一个卷积核，所以作为参数的卷积核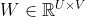对于第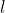层的所有的神经元都是相同的，这也就是卷积神经网络的权重共享特性。
5.1.2 二维卷积算子
在本章面的实现中，算子都继承torch.nn.Module，并使用支持反向传播的pytorchAPI进行实现，这样我们就可以不用手工写backword()的代码实现。
根据公式（5.1），我们首先实现一个简单的二维卷积算子，代码实现如下：
import torch
import torch.nn as nn
class Conv2D(nn.Module):
def __init__(self, kernel_size, weight_attr=torch.tensor([[0., 1.],[2., 3.]])): # 类初始化，初始化权重属性为默认值
super(Conv2D, self).__init__() # 继承torch.nn.Module中的Conv2D卷积算子
self.weight = torch.nn.Parameter(weight_attr)
def forward(self, X):
u, v = self.weight.shape
output = torch.zeros([X.shape[0], X.shape[1] - u + 1, X.shape[2] - v + 1])
for i in range(output.shape[1]):
for j in range(output.shape[2]):
output[:, i, j] = torch.sum(X[:, i:i+u, j:j+v]*self.weight, dim=[1, 2])
return output
# 随机构造一个二维输入矩阵
torch.manual_seed(100)
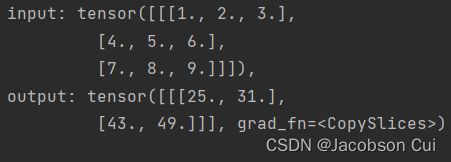
inputs = torch.tensor([[[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]])
conv2d = Conv2D(kernel_size=2)
outputs = conv2d(inputs)
print("input: {}, \noutput: {}".format(inputs, outputs))
运行结果：
5.1.3 二维卷积的参数量和计算量
参数量
由于二维卷积的运算方式为在一个图像（或特征图）上滑动一个卷积核，通过卷积操作得到一组新的特征。所以参数量仅仅与卷积核的尺寸有关，对于一个输入矩阵和一个滤波器，卷积核的参数量为
。
假设有一幅大小为32×32的图像，如果使用全连接前馈网络进行处理，即便第一个隐藏层神经元个数为1，此时该层的参数量也高达1025个，此时该层的计算过程如下图所示。
可以想像，随着隐藏层神经元数量的变多以及层数的加深，使用全连接前馈网络处理图像数据时，参数量会急剧增加。如果使用卷积进行图像处理，当卷积核为3×3时，参数量仅为9相较于全连接前馈网络，参数量少了非常多。
计算量
在卷积神经网络中运算时，通常会统计网络总的乘加运算次数作为计算量（FLOPs，floating point of operations），来衡量整个网络的运算速度。对于单个二维卷积，计算量的统计方式为：
FLOPs=M′×N′×U×V。（5.4）
其中M′×N′表示输出特征图的尺寸，即输出特征图上每个点都要与卷积核进行U×V次乘加运算。对于一幅大小为32×32的图像，使用3×3的卷积核进行运算可以得到以下的输出特征图尺寸：
M′=M−U+1=30M′=M−U+1=30
N′=N−V+1=30N′=N−V+1=30
此时，计算量为：
FLOPs=M′×N′×U×V=30×30×3×3=8100
5.1.4 感受野
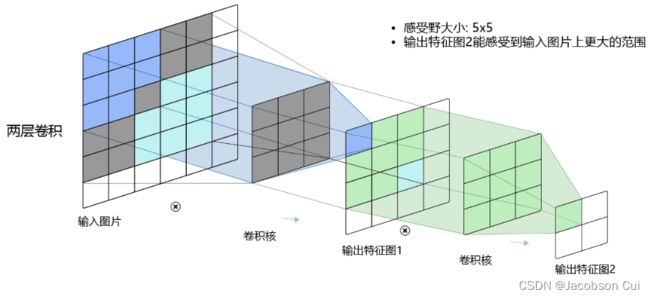
输出特征图上每个点的数值，是由输入图片上大小为U×V的区域的元素与卷积核每个元素相乘再相加得到的，所以输入图像上U×V区域内每个元素数值的改变，都会影响输出点的像素值。我们将这个区域叫做输出特征图上对应点的感受野。感受野内每个元素数值的变动，都会影响输出点的数值变化。比如3×3卷积对应的感受野大小就是3×3，如下图所示。
而当通过两层3×3的卷积之后，感受野的大小将会增加到5×5，如下图所示。
因此，当增加卷积网络深度的同时，感受野将会增大，输出特征图中的一个像素点将会包含更多的图像语义信息。
5.1.5 卷积的变种
在卷积的标准定义基础上，还可以引入卷积核的滑动步长和零填充来增加卷积的多样性，从而更灵活地进行特征抽取。
5.1.5.1 步长（Stride）
在卷积运算的过程中，有时会希望跳过一些位置来降低计算的开销，也可以把这一过程看作是对标准卷积运算输出的下采样。
在计算卷积时，可以在所有维度上每间隔S个元素计算一次，S称为卷积运算的步长（Stride），也就是卷积核在滑动时的间隔。
此时，对于一个输入矩阵和一个滤波器，它们的卷积为
在二维卷积运算中，当步长S=2时，计算过程如下图所示。
5.1.5.2 零填充（Zero Padding）
在卷积运算中，还可以对输入用零进行填充使得其尺寸变大。根据卷积的定义，如果不进行填充，当卷积核尺寸大于1时，输出特征会缩减。对输入进行零填充则可以对卷积核的宽度和输出的大小进行独立的控制。
在二维卷积运算中，零填充（Zero Padding）是指在输入矩阵周围对称地补上P个0。图5.7 为使用零填充的示例。
图5.7：padding=1的零填充
对于一个输入矩阵和一个滤波器，，步长为S，对输入矩阵进行零填充，那么最终输出矩阵大小则为：
引入步长和零填充后的卷积，参数量和计算量的统计方式与之前一致，参数量与卷积核的尺寸有关，为：U×V，计算量与输出特征图和卷积核的尺寸有关，为：
一般常用的卷积有以下三类：
1.窄卷积：步长S=1，两端不补零P=0，卷积后输出尺寸为：
M′=M−U+1,
N′=N−V+1.
2.宽卷积：步长S=1，两端补零P=U−1=V−1，卷积后输出尺寸为：
M′=M+U−1,
N′=N+V−1.
3.等宽卷积：步长S=1，两端补零
，卷积后输出尺寸为：
M′=M,
N′=N.
通常情况下，在层数较深的卷积神经网络，比如：VGG、ResNet中，会使用等宽卷积保证输出特征图的大小不会随着层数的变深而快速缩减。例如：当卷积核的大小为3×3时，会将步长设置为S=1，两端补零P=1，此时，卷积后的输出尺寸就可以保持不变。在本章后续的案例中，会使用ResNet进行实验。
5.1.6 带步长和零填充的二维卷积算子
引入步长和零填充后，二维卷积算子代码实现如下：
class Conv2D(nn.Module):
def __init__(self, kernel_size, stride=1, padding=0, weight_attr=torch.ones([3, 3])):
super(Conv2D, self).__init__()
self.weight = torch.nn.Parameter(weight_attr)
# 步长
self.stride = stride
# 零填充
self.padding = padding
def forward(self, X):
# 零填充
new_X = torch.zeros([X.shape[0], X.shape[1]+2*self.padding, X.shape[2]+2*self.padding])
new_X[:, self.padding:X.shape[1]+self.padding, self.padding:X.shape[2]+self.padding] = X
u, v = self.weight.shape
output_w = (new_X.shape[1] - u) // self.stride + 1
output_h = (new_X.shape[2] - v) // self.stride + 1
output = torch.zeros([X.shape[0], output_w, output_h])
for i in range(0, output.shape[1]):
for j in range(0, output.shape[2]):
output[:, i, j] = torch.sum(new_X[:, self.stride*i:self.stride*i+u, self.stride*j:self.stride*j+v]*self.weight, dim=[1, 2])
return output
inputs = torch.randn([2, 8, 8])
conv2d_padding = Conv2D(kernel_size=3, padding=1)
outputs = conv2d_padding(inputs)
print("When kernel_size=3, padding=1 stride=1, input's shape: {}, output's shape: {}".format(inputs.shape, outputs.shape))
conv2d_stride = Conv2D(kernel_size=3, stride=2, padding=1)
outputs = conv2d_stride(inputs)
print("When kernel_size=3, padding=1 stride=2, input's shape: {}, output's shape: {}".format(inputs.shape, outputs.shape))运行结果：
从输出结果看出，使用3×3大小卷积，padding为1，当stride=1时，模型的输出特征图可以与输入特征图保持一致；当stride=2时，输出特征图的宽和高都缩小一倍。
5.1.7 使用卷积运算完成图像边缘检测任务
在图像处理任务中，常用拉普拉斯算子对物体边缘进行提取，拉普拉斯算子为一个大小为3×3的卷积核，中心元素值是8，其余元素值是−1。
考虑到边缘其实就是图像上像素值变化很大的点的集合，因此可以通过计算二阶微分得到，当二阶微分为0时，像素值的变化最大。此时，对x方向和y方向分别求取二阶导数：
完整的二阶微分公式为：
上述公式也被称为拉普拉斯算子，对应的二阶微分卷积核为：
对上述算子全部求反也可以起到相同的作用，此时，该算子可以表示为：
也就是一个点的四邻域拉普拉斯的算子计算结果是自己像素值的四倍减去上下左右的像素的和，将这个算子旋转45°后与原算子相加，就变成八邻域的拉普拉斯算子，也就是一个像素自己值的八倍减去周围一圈八个像素值的和，做为拉普拉斯计算结果，此时，该算子可以表示为：
下面我们利用上面定义的Conv2D算子，构造一个简单的拉普拉斯算子，并对一张输入的灰度图片进行边缘检测，提取出目标的外形轮廓。
import matplotlib.pyplot as plt
from PIL import Image
import numpy as np
# 读取图片
img = Image.open('number.jpg').resize((256, 256))
# 设置卷积核参数
w = np.array([[-1,-1,-1], [-1,8,-1], [-1,-1,-1]], dtype='float32')
# 创建卷积算子，卷积核大小为3x3，并使用上面的设置好的数值作为卷积核权重的初始化参数
conv = Conv2D(kernel_size=3, stride=1, padding=0, weight_attr=torch.tensor(w))
# 将读入的图片转化为float32类型的numpy.ndarray
inputs = np.array(img).astype('float32')
print("bf to_tensor, inputs:",inputs)
# 将图片转为Tensor
inputs = torch.tensor(inputs)
print("bf unsqueeze, inputs:",inputs)
inputs = torch.unsqueeze(inputs, dim=0)
print("af unsqueeze, inputs:",inputs)
outputs = conv(inputs)
# 可视化结果
plt.figure(figsize=(8, 4))
f = plt.subplot(121)
f.set_title('input image', fontsize=15)
plt.imshow(img)
f = plt.subplot(122)
f.set_title('output feature map', fontsize=15)
plt.imshow(outputs.detach().numpy().squeeze(), cmap='gray')
plt.savefig('conv-vis.pdf')
plt.show()运行结果：
从输出结果看，使用拉普拉斯算子，目标的边缘可以成功被检测出来。
边缘检测系列1：传统边缘检测算子
使用 Paddle 实现一些传统边缘检测算子，如：Roberts、Prewitt、Sobel、Scharr、Kirsch、Robinson、Laplacian
引入
-
图像的边缘指的是灰度值发生急剧变化的位置。
-
在图像形成过程中，由于亮度、纹理、颜色、阴影等物理因素的不同而导致图像灰度值发生突变，从而形成边缘。
-
边缘是通过检查每个像素的邻域并对其灰度变化进行量化的，这种灰度变化的量化相当于微积分里连续函数中方向导数或者离散数列的差分。
算法原理
-
传统的边缘检测大多数是通过基于方向导数掩码（梯度方向导数）求卷积的方法。
-
计算灰度变化的卷积算子包含Roberts算子、Prewitt算子、Sobel算子、Scharr算子、Kirsch算子、Robinson算子、Laplacian算子。
-
大多数边缘检测算子是基于方向差分卷积核求卷积的方法，在使用由两个或者多个卷积核组成的边缘检测算子时假设有 n 个卷积核，记
，为图像分别与个卷积核做卷积的结果，通常有四种方式来衡量最后输出的边缘强度。-
取对应位置绝对值的和：
-
取对应位置平方和的开方：
-
取对应位置绝对值的最大值：
-
插值法：
，其中
，且
-
代码实现
构建通用的边缘检测算子
因为上述的这些算子在本质上都是通过卷积计算实现的，只是所使用到的卷积核参数有所不同,所以可以构建一个通用的计算算子，只需要传入对应的卷积核参数即可实现不同的边缘检测,并且在后处理时集成了上述的四种计算最终边缘强度的方式。
import numpy as np
import torch
import torch.nn as nn
class EdgeOP(nn.Module):
def __init__(self, kernel):
super(EdgeOP, self).__init__()
out_channels, in_channels, h, w = kernel.shape
self.filter = nn.Conv2D(in_channels=in_channels, out_channels=out_channels, kernel_size=(h, w), padding='SAME', bias_attr=False)
self.filter.weight.set_value(kernel.astype('float32'))
@staticmethod
def postprocess(outputs, mode=0, weight=None):
if mode == 0:
results = torch.sum(torch.abs(outputs), dim=1)
elif mode == 1:
results = torch.sqrt(torch.sum(torch.pow(outputs, 2), dim=1))
elif mode == 2:
results = torch.max(torch.abs(outputs), dim=1)
elif mode == 3:
if weight is None:
C = outputs.shape[1]
weight = torch.tensor([1 / C] * C, dtype=torch.float32)
else:
weight = torch.tensor(weight, dtype=torch.float32)
results = torch.einsum('nchw, c -> nhw', torch.abs(outputs), weight)
elif mode == 4:
results = torch.abs(outputs)
return torch.clip(results, 0, 255).cast('uint8')
@torch.no_grad()
def forward(self, images, mode=0, weight=None):
outputs = self.filter(images)
return self.postprocess(outputs, mode, weight)图像边缘检测测试函数
为了方便测试就构建了如下的测试函数，测试同一张图片不同算子/不同边缘强度计算方法的边缘检测效果。
import os
import cv2
from PIL import Image
import matplotlib.pyplot as plt
def test_edge_det(kernel, img_path='2.jpg'):
img = cv2.imread(img_path, 0)
img_tensor = torch.tensor(img, dtype=torch.float32)[None, None, ...]
op = EdgeOP(kernel)
all_results = []
for mode in range(4):
results = op(img_tensor, mode=mode)
all_results.append(results.numpy()[0])
results = op(img_tensor, mode=4)
for result in results.numpy()[0]:
all_results.append(result)
return all_results, np.concatenate(all_results, 1)Roberts 算子
roberts_kernel = np.array([
[[
[1, 0],
[0, -1]
]],
[[
[0, -1],
[1, 0]
]]
])
_, concat_res = test_edge_det(roberts_kernel)
Image.fromarray(concat_res).show()运行结果：
Prewitt 算子
prewitt_kernel = np.array([
[[
[-1, -1, -1],
[ 0, 0, 0],
[ 1, 1, 1]
]],
[[
[-1, 0, 1],
[-1, 0, 1],
[-1, 0, 1]
]],
[[
[ 0, 1, 1],
[-1, 0, 1],
[-1, -1, 0]
]],
[[
[ -1, -1, 0],
[ -1, 0, 1],
[ 0, 1, 1]
]]
])
_, concat_res = test_edge_det(prewitt_kernel)
Image.fromarray(concat_res).show()运行结果：
Sobel 算子
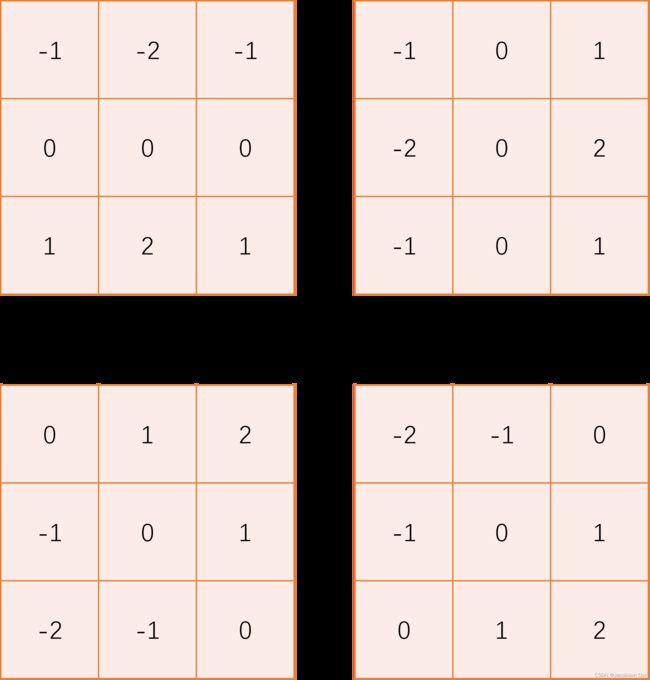
sobel_kernel = np.array([
[[
[-1, -2, -1],
[ 0, 0, 0],
[ 1, 2, 1]
]],
[[
[-1, 0, 1],
[-2, 0, 2],
[-1, 0, 1]
]],
[[
[ 0, 1, 2],
[-1, 0, 1],
[-2, -1, 0]
]],
[[
[ -2, -1, 0],
[ -1, 0, 1],
[ 0, 1, 2]
]]
])
_, concat_res = test_edge_det(sobel_kernel)
Image.fromarray(concat_res).show()运行结果：
Scharr 算子
scharr_kernel = np.array([
[[
[-3, -10, -3],
[ 0, 0, 0],
[ 3, 10, 3]
]],
[[
[-3, 0, 3],
[-10, 0, 10],
[-3, 0, 3]
]],
[[
[ 0, 3, 10],
[-3, 0, 3],
[-10, -3, 0]
]],
[[
[ -10, -3, 0],
[ -3, 0, 3],
[ 0, 3, 10]
]]
])
_, concat_res = test_edge_det(scharr_kernel)
Image.fromarray(concat_res).show()运行结果：
Krisch 算子
Krisch_kernel = np.array([
[[
[5, 5, 5],
[-3,0,-3],
[-3,-3,-3]
]],
[[
[-3, 5,5],
[-3,0,5],
[-3,-3,-3]
]],
[[
[-3,-3,5],
[-3,0,5],
[-3,-3,5]
]],
[[
[-3,-3,-3],
[-3,0,5],
[-3,5,5]
]],
[[
[-3, -3, -3],
[-3,0,-3],
[5,5,5]
]],
[[
[-3, -3, -3],
[5,0,-3],
[5,5,-3]
]],
[[
[5, -3, -3],
[5,0,-3],
[5,-3,-3]
]],
[[
[5, 5, -3],
[5,0,-3],
[-3,-3,-3]
]],
])
_, concat_res = test_edge_det(Krisch_kernel)
Image.fromarray(concat_res).show()运行结果：
Robinson算子 
robinson_kernel = np.array([
[[
[1, 2, 1],
[0, 0, 0],
[-1, -2, -1]
]],
[[
[0, 1, 2],
[-1, 0, 1],
[-2, -1, 0]
]],
[[
[-1, 0, 1],
[-2, 0, 2],
[-1, 0, 1]
]],
[[
[-2, -1, 0],
[-1, 0, 1],
[0, 1, 2]
]],
[[
[-1, -2, -1],
[0, 0, 0],
[1, 2, 1]
]],
[[
[0, -1, -2],
[1, 0, -1],
[2, 1, 0]
]],
[[
[1, 0, -1],
[2, 0, -2],
[1, 0, -1]
]],
[[
[2, 1, 0],
[1, 0, -1],
[0, -1, -2]
]],
])
_, concat_res = test_edge_det(robinson_kernel)
Image.fromarray(concat_res).show()运行结果：
Laplacian 算子
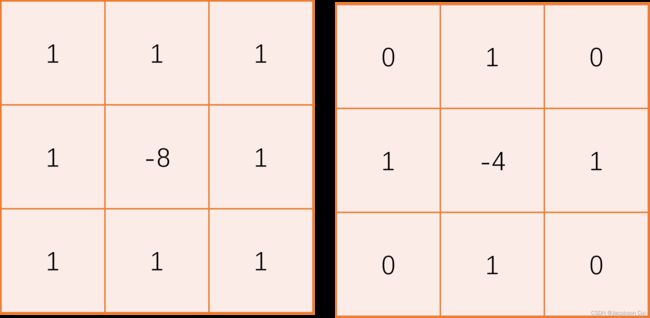
laplacian_kernel = np.array([
[[
[1, 1, 1],
[1, -8, 1],
[1, 1, 1]
]],
[[
[0, 1, 0],
[1, -4, 1],
[0, 1, 0]
]]
])
_, concat_res = test_edge_det(laplacian_kernel)
Image.fromarray(concat_res).show()运行结果：
边缘检测系列2：简易的 Canny 边缘检测器
基于 Numpy / Paddle 实现的简易的 Canny 边缘检测算法
引入
- 边缘检测是图像处理中一个基础的算法
- 常用的边缘检测算法有 Sobel、Prewitt、Roberts、Canny、Marr-Hildreth 等
- 本次就简单介绍一下经典的 Canny 边缘检测算法和其实现方法
算法原理
-
Canny 是一个经典的图像边缘检测算法，一般包含如下几个步骤：
-
使用高斯模糊对图像进行模糊降噪处理
-
基于图像梯度幅值进行图像边缘增强
-
非极大值抑制处理进行图像边缘细化
-
图像二值化和边缘连接得到最终的结果
-
代码实现
基于 OpenCV 实现快速的 Canny 边缘检测
- 在 OpenCV 中只需要使用 cv2.Canny 函数即可实现 Canny 边缘检测
import cv2
import numpy as np
from PIL import Image
lower = 30 # 最小阈值
upper = 70 # 最大阈值
img_path = 'number.jpg' # 指定测试图像路径
gray = cv2.imread(img_path, 0) # 读取灰度图像
edge = cv2.Canny(gray, lower, upper) # Canny 图像边缘检测
contrast = np.concatenate([edge, gray], 1) # 图像拼接
Image.fromarray(contrast).show()运行结果：
基于 Numpy 模块实现简单的 Canny 检测器
import cv2
import math
import numpy as np
from PIL import Image
def smooth(img_gray, kernel_size=5):
# 生成高斯滤波器
"""
要生成一个 (2k+1)x(2k+1) 的高斯滤波器，滤波器的各个元素计算公式如下：
H[i, j] = (1/(2*pi*sigma**2))*exp(-1/2*sigma**2((i-k-1)**2 + (j-k-1)**2))
"""
sigma1 = sigma2 = 1.4
gau_sum = 0
gaussian = np.zeros([kernel_size, kernel_size])
for i in range(kernel_size):
for j in range(kernel_size):
gaussian[i, j] = math.exp(
(-1 / (2 * sigma1 * sigma2)) *
(np.square(i - 3) + np.square(j-3))
) / (2 * math.pi * sigma1 * sigma2)
gau_sum = gau_sum + gaussian[i, j]
# 归一化处理
gaussian = gaussian / gau_sum
# 高斯滤波
img_gray = np.pad(img_gray, ((kernel_size//2, kernel_size//2), (kernel_size//2, kernel_size//2)), mode='constant')
W, H = img_gray.shape
new_gray = np.zeros([W - kernel_size, H - kernel_size])
for i in range(W-kernel_size):
for j in range(H-kernel_size):
new_gray[i, j] = np.sum(
img_gray[i: i + kernel_size, j: j + kernel_size] * gaussian
)
return new_gray
def gradients(new_gray):
"""
:type: image which after smooth
:rtype:
dx: gradient in the x direction
dy: gradient in the y direction
M: gradient magnitude
theta: gradient direction
"""
W, H = new_gray.shape
dx = np.zeros([W-1, H-1])
dy = np.zeros([W-1, H-1])
M = np.zeros([W-1, H-1])
theta = np.zeros([W-1, H-1])
for i in range(W-1):
for j in range(H-1):
dx[i, j] = new_gray[i+1, j] - new_gray[i, j]
dy[i, j] = new_gray[i, j+1] - new_gray[i, j]
# 图像梯度幅值作为图像强度值
M[i, j] = np.sqrt(np.square(dx[i, j]) + np.square(dy[i, j]))
# 计算 θ - artan(dx/dy)
theta[i, j] = math.atan(dx[i, j] / (dy[i, j] + 0.000000001))
return dx, dy, M, theta
def NMS(M, dx, dy):
d = np.copy(M)
W, H = M.shape
NMS = np.copy(d)
NMS[0, :] = NMS[W-1, :] = NMS[:, 0] = NMS[:, H-1] = 0
for i in range(1, W-1):
for j in range(1, H-1):
# 如果当前梯度为0，该点就不是边缘点
if M[i, j] == 0:
NMS[i, j] = 0
else:
gradX = dx[i, j] # 当前点 x 方向导数
gradY = dy[i, j] # 当前点 y 方向导数
gradTemp = d[i, j] # 当前梯度点
# 如果 y 方向梯度值比较大，说明导数方向趋向于 y 分量
if np.abs(gradY) > np.abs(gradX):
weight = np.abs(gradX) / np.abs(gradY) # 权重
grad2 = d[i-1, j]
grad4 = d[i+1, j]
# 如果 x, y 方向导数符号一致
# 像素点位置关系
# g1 g2
# c
# g4 g3
if gradX * gradY > 0:
grad1 = d[i-1, j-1]
grad3 = d[i+1, j+1]
# 如果 x，y 方向导数符号相反
# 像素点位置关系
# g2 g1
# c
# g3 g4
else:
grad1 = d[i-1, j+1]
grad3 = d[i+1, j-1]
# 如果 x 方向梯度值比较大
else:
weight = np.abs(gradY) / np.abs(gradX)
grad2 = d[i, j-1]
grad4 = d[i, j+1]
# 如果 x, y 方向导数符号一致
# 像素点位置关系
# g3
# g2 c g4
# g1
if gradX * gradY > 0:
grad1 = d[i+1, j-1]
grad3 = d[i-1, j+1]
# 如果 x，y 方向导数符号相反
# 像素点位置关系
# g1
# g2 c g4
# g3
else:
grad1 = d[i-1, j-1]
grad3 = d[i+1, j+1]
# 利用 grad1-grad4 对梯度进行插值
gradTemp1 = weight * grad1 + (1 - weight) * grad2
gradTemp2 = weight * grad3 + (1 - weight) * grad4
# 当前像素的梯度是局部的最大值，可能是边缘点
if gradTemp >= gradTemp1 and gradTemp >= gradTemp2:
NMS[i, j] = gradTemp
else:
# 不可能是边缘点
NMS[i, j] = 0
return NMS
def double_threshold(NMS, threshold1, threshold2):
NMS = np.pad(NMS, ((1, 1), (1, 1)), mode='constant')
W, H = NMS.shape
DT = np.zeros([W, H])
# 定义高低阈值
TL = threshold1 * np.max(NMS)
TH = threshold2 * np.max(NMS)
for i in range(1, W-1):
for j in range(1, H-1):
# 双阈值选取
if (NMS[i, j] < TL):
DT[i, j] = 0
elif (NMS[i, j] > TH):
DT[i, j] = 1
# 连接
elif ((NMS[i-1, j-1:j+1] < TH).any() or
(NMS[i+1, j-1:j+1].any() or
(NMS[i, [j-1, j+1]] < TH).any())):
DT[i, j] = 1
return DT
def canny(gray, threshold1, threshold2, kernel_size=5):
norm_gray = gray
gray_smooth = smooth(norm_gray, kernel_size)
dx, dy, M, theta = gradients(gray_smooth)
nms = NMS(M, dx, dy)
DT = double_threshold(nms, threshold1, threshold2)
return DT
import cv2
import numpy as np
from PIL import Image
lower = 0.1 # 最小阈值
upper = 0.3 # 最大阈值
img_path = '2.jpg' # 指定测试图像路径
gray = cv2.imread(img_path, 0) # 读取灰度图像
edge = canny(gray, lower, upper) # Canny 图像边缘检测
edge = (edge * 255).astype(np.uint8) # 反归一化
contrast = np.concatenate([edge, gray], 1) # 图像拼接
Image.fromarray(contrast).show()运行结果：
基于 Pytorch 实现的 Canny 边缘检测器
import torch
import torch.nn as nn
import math
import cv2
import numpy as np
from scipy.signal import gaussian
from PIL import Image
def get_state_dict(filter_size=5, std=1.0, map_func=lambda x: x):
generated_filters = gaussian(filter_size, std=std).reshape([1, filter_size]).astype(np.float32)
gaussian_filter_horizontal = generated_filters[None, None, ...]
gaussian_filter_vertical = generated_filters.T[None, None, ...]
sobel_filter_horizontal = np.array([[[
[1., 0., -1.],
[2., 0., -2.],
[1., 0., -1.]]]],
dtype='float32'
)
sobel_filter_vertical = np.array([[[
[1., 2., 1.],
[0., 0., 0.],
[-1., -2., -1.]]]],
dtype='float32'
)
directional_filter = np.array(
[[[[0., 0., 0.],
[0., 1., -1.],
[0., 0., 0.]]],
[[[0., 0., 0.],
[0., 1., 0.],
[0., 0., -1.]]],
[[[0., 0., 0.],
[0., 1., 0.],
[0., -1., 0.]]],
[[[0., 0., 0.],
[0., 1., 0.],
[-1., 0., 0.]]],
[[[0., 0., 0.],
[-1., 1., 0.],
[0., 0., 0.]]],
[[[-1., 0., 0.],
[0., 1., 0.],
[0., 0., 0.]]],
[[[0., -1., 0.],
[0., 1., 0.],
[0., 0., 0.]]],
[[[0., 0., -1.],
[0., 1., 0.],
[0., 0., 0.]]]],
dtype=np.float32
)
connect_filter = np.array([[[
[1., 1., 1.],
[1., 0., 1.],
[1., 1., 1.]]]],
dtype=np.float32
)
return {
'gaussian_filter_horizontal.weight': map_func(gaussian_filter_horizontal),
'gaussian_filter_vertical.weight': map_func(gaussian_filter_vertical),
'sobel_filter_horizontal.weight': map_func(sobel_filter_horizontal),
'sobel_filter_vertical.weight': map_func(sobel_filter_vertical),
'directional_filter.weight': map_func(directional_filter),
'connect_filter.weight': map_func(connect_filter)
}
class CannyDetector(nn.Module):
def __init__(self, filter_size=5, std=1.0, device='cpu'):
super(CannyDetector, self).__init__()
# 配置运行设备
self.device = device
# 高斯滤波器
self.gaussian_filter_horizontal = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=(1, filter_size),
padding=(0, filter_size // 2), bias=False)
self.gaussian_filter_vertical = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=(filter_size, 1),
padding=(filter_size // 2, 0), bias=False)
# Sobel 滤波器
self.sobel_filter_horizontal = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3, padding=1, bias=False)
self.sobel_filter_vertical = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3, padding=1, bias=False)
# 定向滤波器
self.directional_filter = nn.Conv2d(in_channels=1, out_channels=8, kernel_size=3, padding=1, bias=False)
# 连通滤波器
self.connect_filter = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3, padding=1, bias=False)
# 初始化参数
params = get_state_dict(filter_size=filter_size, std=std,
map_func=lambda x: torch.from_numpy(x).to(self.device))
self.load_state_dict(params)
@torch.no_grad()
def forward(self, img, threshold1=10.0, threshold2=100.0):
# 拆分图像通道
img_r = img[:, 0:1] # red channel
img_g = img[:, 1:2] # green channel
img_b = img[:, 2:3] # blue channel
# Step1: 应用高斯滤波进行模糊降噪
blur_horizontal = self.gaussian_filter_horizontal(img_r)
blurred_img_r = self.gaussian_filter_vertical(blur_horizontal)
blur_horizontal = self.gaussian_filter_horizontal(img_g)
blurred_img_g = self.gaussian_filter_vertical(blur_horizontal)
blur_horizontal = self.gaussian_filter_horizontal(img_b)
blurred_img_b = self.gaussian_filter_vertical(blur_horizontal)
# Step2: 用 Sobel 算子求图像的强度梯度
grad_x_r = self.sobel_filter_horizontal(blurred_img_r)
grad_y_r = self.sobel_filter_vertical(blurred_img_r)
grad_x_g = self.sobel_filter_horizontal(blurred_img_g)
grad_y_g = self.sobel_filter_vertical(blurred_img_g)
grad_x_b = self.sobel_filter_horizontal(blurred_img_b)
grad_y_b = self.sobel_filter_vertical(blurred_img_b)
# Step2: 确定边缘梯度和方向
grad_mag = torch.sqrt(grad_x_r ** 2 + grad_y_r ** 2)
grad_mag += torch.sqrt(grad_x_g ** 2 + grad_y_g ** 2)
grad_mag += torch.sqrt(grad_x_b ** 2 + grad_y_b ** 2)
grad_orientation = (
torch.atan2(grad_y_r + grad_y_g + grad_y_b, grad_x_r + grad_x_g + grad_x_b) * (180.0 / math.pi))
grad_orientation += 180.0
grad_orientation = torch.round(grad_orientation / 45.0) * 45.0
# Step3: 非最大抑制，边缘细化
all_filtered = self.directional_filter(grad_mag)
inidices_positive = (grad_orientation / 45) % 8
inidices_negative = ((grad_orientation / 45) + 4) % 8
batch, _, height, width = inidices_positive.shape
pixel_count = height * width * batch
pixel_range = torch.Tensor([range(pixel_count)]).to(self.device)
indices = (inidices_positive.reshape((-1,)) * pixel_count + pixel_range).squeeze()
channel_select_filtered_positive = all_filtered.reshape((-1,))[indices.long()].reshape(
(batch, 1, height, width))
indices = (inidices_negative.reshape((-1,)) * pixel_count + pixel_range).squeeze()
channel_select_filtered_negative = all_filtered.reshape((-1,))[indices.long()].reshape(
(batch, 1, height, width))
channel_select_filtered = torch.stack([channel_select_filtered_positive, channel_select_filtered_negative])
is_max = channel_select_filtered.min(dim=0)[0] > 0.0
thin_edges = grad_mag.clone()
thin_edges[is_max == 0] = 0.0
# Step4: 双阈值
low_threshold = min(threshold1, threshold2)
high_threshold = max(threshold1, threshold2)
thresholded = thin_edges.clone()
lower = thin_edges < low_threshold
thresholded[lower] = 0.0
higher = thin_edges > high_threshold
thresholded[higher] = 1.0
connect_map = self.connect_filter(higher.float())
middle = torch.logical_and(thin_edges >= low_threshold, thin_edges <= high_threshold)
thresholded[middle] = 0.0
connect_map[torch.logical_not(middle)] = 0
thresholded[connect_map > 0] = 1.0
thresholded[..., 0, :] = 0.0
thresholded[..., -1, :] = 0.0
thresholded[..., :, 0] = 0.0
thresholded[..., :, -1] = 0.0
thresholded = (thresholded > 0.0).float()
return thresholded
lower = 2.5 # 最小阈值
upper = 5 # 最大阈值
img_path = '2.jpg' # 指定测试图像路径
img = cv2.imread(img_path, 1) # 读取彩色图像
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) # 转为灰度图
img = np.transpose(img, [2, 1, 0]) / 255.0 # 转置 + 归一化
img_tensor = torch.tensor(img[None, ...], dtype=torch.float32) # 转换为 Tensor
canny = CannyDetector() # 初始化 Canny 检测器
edge = canny(img_tensor, lower, upper) # Canny 图像边缘检测
edge = np.squeeze(edge.numpy()) # 去除 Batch dim
edge = np.transpose(edge, [1, 0]) # 图像转置
edge = (edge * 255).astype(np.uint8) # 反归一化
contrast = np.concatenate([edge, gray], 1) # 图像拼接
Image.fromarray(contrast).show()运行结果：
边缘检测系列3：【HED】 Holistically-Nested 边缘检测
-
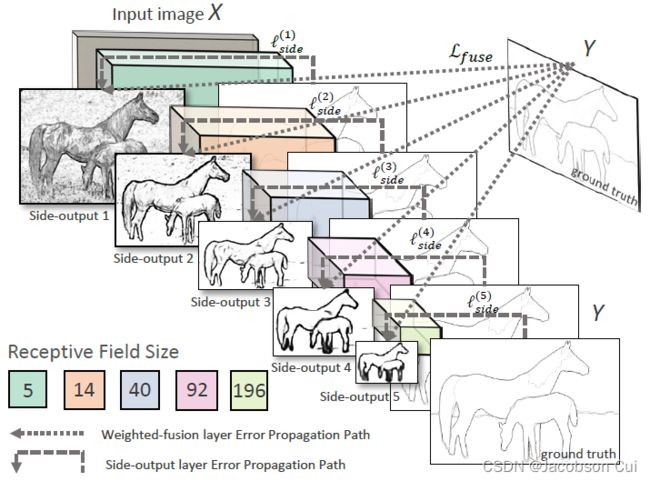
HED 模型包含五个层级的特征提取架构，每个层级中：
-
使用 VGG Block 提取层级特征图
-
使用层级特征图计算层级输出
-
层级输出上采样
-
-
最后融合五个层级输出作为模型的最终输出：
-
通道维度拼接五个层级的输出
-
1x1 卷积对层级输出进行融合
-
-
模型总体架构图如下：
HED通过深度学习网络实现边缘检测，网络主要有以下两个特点：
（1）Holistically：指端到端（end-to-end 或者image-to-image）的学习方式，也就是说，网络的输入为原图，输出为边缘检测得到的二值化图像。
（2）Nested：意思是嵌套的。在论文中指，在每层卷积层后输出该层的结果（responses produced at hidden layers ），这个结果在论文中称为side outputs。不同隐藏层的Side output尺度不同，而且HED不止要求最后输出的边缘图像好，也要求各side output的结果要好，即学习对象是最终的输出和各Side outputs。
HED是在VGG网络基础上改造的，卷积层后添加side output。网络层次越深，卷积核越大，side output越小，最终的输出是对多个side output特征的融合。
HED和Canny的处理结果进行比较：
从处理结果的展示中可以看到HED的精度高于Canny。Canny的精度主要依赖于阈值的设置，通过人为的阈值设置可以检测到细粒度的边缘，很依赖图片像素值。但是相比于神经网络，Canny缺失语义方面的理解，神经网络对边缘的理解是更多层次的。HED属于深度学习网络的一种，而且加入了Deep supervision，每个Side output继承上一层的特征，最后对多层特征融合，进一步取得了精度的提升。
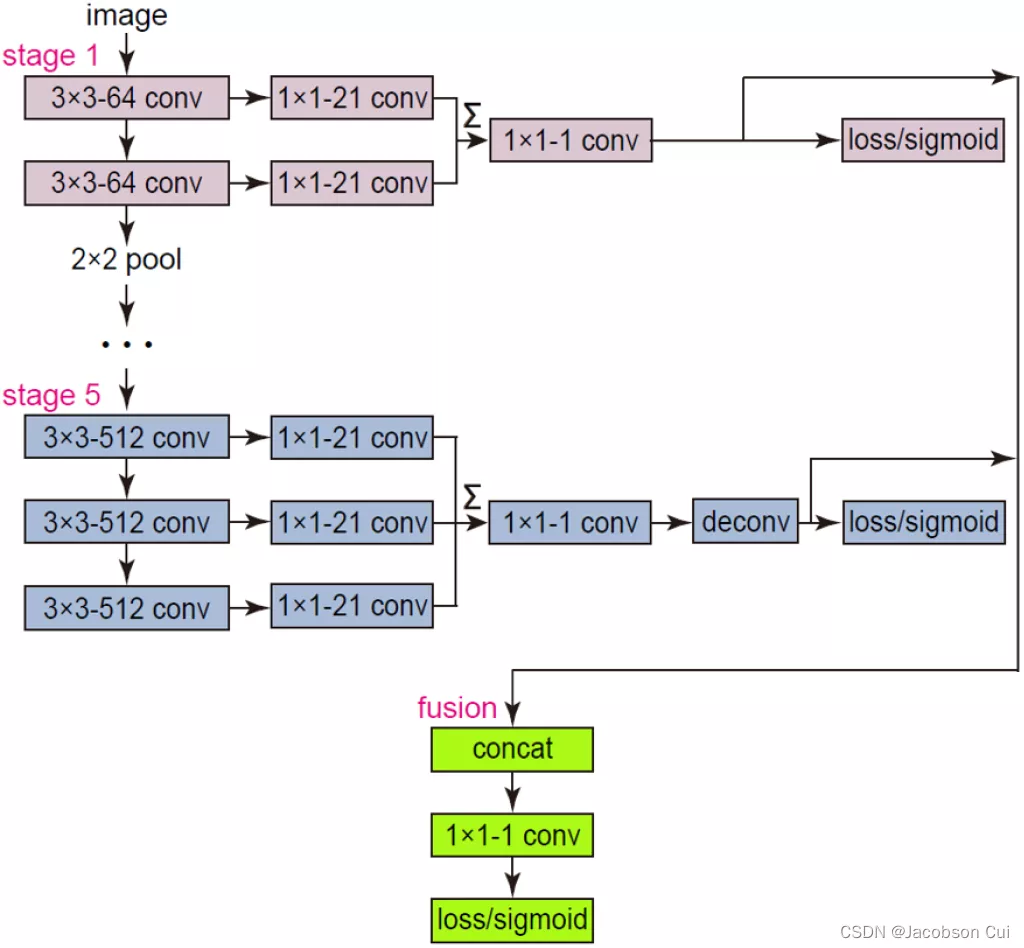
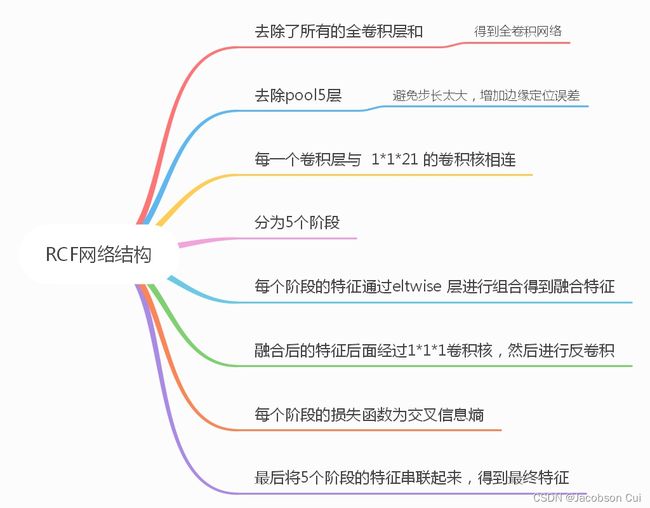
边缘检测系列4：【RCF】基于更丰富的卷积特征的边缘检测
-
RCF 与 HED 模型一样，包含五个层级的特征提取架构，同样也是基于 VGG 16 Backbone
-
相比 HED，RCF 模型更加充分利用对象的多尺度和多级信息来全面地执行图像到图像的预测
-
RCF 不只是使用了每个层级的输出，而是使用了每个层级中所有卷积层的输出进行融合（Conv + sum）后，作为边缘检测的输入
-
模型结构图如下：
RCF的网络结构特点：
在 RCF网络中，所有的卷积层都被很好的集成到最终的特征表hi中，而这种方式可以通过反向传播进行训练。VGG16中的每层卷积的感受野的尺寸皆不相同，RCF比现有的方法的优点之处在于它的机制可以更好的去学习多尺度的信息，这些信息分别来自于不同层次的卷积特征。在RCF中，深层次的特征比较粗糙，对于较大的目标以及目标的部分边缘处可以得到比较强的响应。同时，浅层的特征可以为深层特征补充充分的细节信息。
RCF与HED的不同点：
1、HED对于边缘检测来说，丢失了许多非常有用的信息，因为它仅使用到VGG16中每个阶段的最后一层卷积特征。RCF与之相反，它使用了所有卷积层的特征，使得在更大的范围内捕获更多的对象或对象局部边界成为可能。
2、RCF创造性的提出了一个对训练样本非常合适的损失函数。而且，本文首先将标注人数大于A的边缘像素作为正样例，为0的作为负样例。除此之外，还忽略了标注者人数小于A的边缘像素，既不作为正样例，也不作为负样例。与之相反的是，HED将标注人数小于总人数一半的边缘像素作为负样例。上述做法会迷惑网络的训练，因为这些点并不是真实的分边缘像素点。
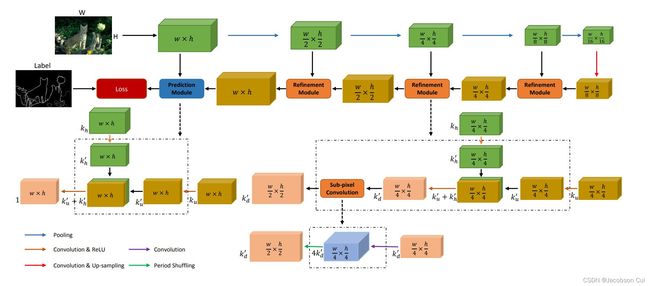
边缘检测系列5：【CED】添加了反向细化路径的 HED 模型
-
CED 模型总体基于 HED 模型改造而来，其中做了如下几个改进：
-
将模型中的上采样操作从转置卷积插值更换为 PixelShuffle
-
添加了反向细化路径，即一个反向的从高层级特征逐步往低层级特征的边缘细化路径
-
没有多层级输出，最终的输出为融合了各层级的特征的边缘检测结果
-
-
架构图如下：
CED的两个主要组成部分：前向传播路径和反向细化路径。 前向传播路径类似于HED。 它生成具有丰富语义信息的高维低分辨率特征图。 反向细化路径将沿着向前传播路径的特征图与中间特征进行融合。 这个细化是通过细化模块多次完成的。 每次我们使用子像素卷积将特征分辨率提高一个小的因子（2x），最终达到输入分辨率。
- 一方面是前馈传播，获取丰富的网络特征图，而一大特点是，用了一个反向细化路径（backward-refining path，也就是图中的橙色框，扩展开就是第二个虚线框中的结构）来补充HED网络，它使用有效的亚像素卷积逐步提高样本特征， 反向细化路径将特征映射与沿前向传播路径的中间特征融合，这个细化方式由多个细化模块一起组成，最终达到原图的分辨率。
- 细化模块融合了一个自顶向下的特征映射和前传上的特征映射，并使用亚像素卷积向上采样。在进行融合的时候，通过减少两个特征映射的维数来实现融合（即降维，由于通道数不同，不得不这样做）。
- 将输入前向路径特征映射的通道数表示为kh。 经过卷积和RELU运算后，信道被简化为k‘h，远小于kh。同样的操作从先前的细化模块对特征映射进行校正，从ku生成k‘u。将上述特征映射连接到一个新的具有k‘u+k’h通道的特征映射中，并将其减少，用k‘d通道通过3×3卷积层进行特征映射。从而降低了总体计算成本，平衡了两个输入特征映射。
- 对于上采样，采用亚像素卷积操作，而非流行的反卷积操作，这样对于边缘的定位表现似乎更好。亚像素卷积不是通过单个反卷积层直接输出放大特征映射，而是由一个卷积层和一个跟随相移层组成的一种网络层。总体上看，参数量也比HED少了许多。
- 参考来源：Deep Crisp Boundaries（CED）论文学习笔记_小风_的博客-CSDN博客
参考资料
论文笔记 HED：Holistically-Nested Edge Detection_潇湘_AQ的博客-CSDN博客_hed算法
Richer Convolutional Features for Edge Detection 论文阅读_DoublleTree的博客-CSDN博客
论文笔记（2）：Deep Crisp Boundaries: From Boundaries to Higher-level Tasks