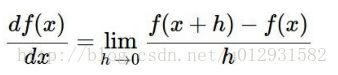cs231n-梯度下降及在线性分类器的应用
梯度下降法
- 梯度下降法
- 数值梯度
- 分析梯度
- svm loss
- Softmax loss
- 梯度检验
- mini-batch 梯度下降
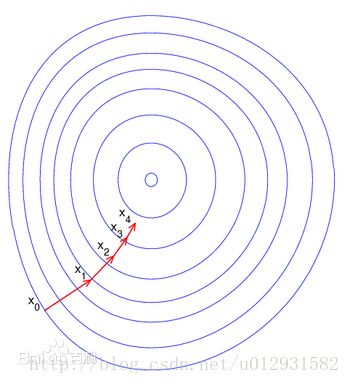
如果学过最优化,那么就知道梯度下降法是最简单的一种函数求极小的方法,也成为最速下降法,过程如下,首先选取一个初始位置,计算当前位置下的函数的梯度,然后按照负梯度方向走一个步长的距离,重新在当前点计算梯度并走一个负梯度方向的步长,迭代当前过程直到收敛. 过程可以用下图表示:
还是举一个图片分类的例子,当前一共有10类的图片,每一张图片都有相同的大小32*32*3=3072维.数据集如下所示:
分类过程如下图所示,其中权值矩阵是一个10*3072大小的矩阵, xi 是一个3072*1的向量,b为10*1的向量,分别对应这10个类别的偏置,然后通过
f(xi;W,b)=Wxi+b
这样一个打分函数计算出当前图片对应10个类的分数,选取分数最高的一类作为最后的分类结果,过程如下图所示:
线性分类器都是这样一个计算过程, 只不过不同的线性分类器对应这不同的损失函数,损失函数我们在上一节已经介绍过了,
Svm Loss: Li=∑j≠yimax(0,wTjxi−wTyixi+Δ))
Total Loss: L=1N∑Li+λ∑∑Wkj2
Softmax Loss: Li=−log(ewTyixi∑kewjxi)
Total Loss: L=1N∑Li
在线性分类器优化的过程中,损失函数就是目标函数,优化的目的就是使得损失函数最小.
在实际的应用过程中,梯度下降法有两种应用的形式,一种是数值梯度,另外一种是分析梯度.
数值梯度
计算梯度的公式如下:
这个是最基本的公式,两种计算方法都是根据这个公式来的.
在计算数值梯度的过程中,通常选取一个比较小的h,计算出 f(x+h) 然后按照上述公式进行计算梯度.
过程如下:
首先已知当前的权值矩阵,W为一个10*3072的矩阵,dW也是同样的大小.
在当前位置,需要求W的每一个分量的梯度,所以就需要分别对每一个位置加上h(每次只计算一个分量),计算L(W+h)然后通过上述公式进行求梯度,计算过程如下:
这样就求得了第一个位置的梯度,之后计算第二个位置的梯度:
也就是说如果要求当前W的梯度,需要计算10*3072次.这种方法虽然计算结果是正确的,但是在实际计算过程中当然是不实用的,因为计算量实在是太大,这也就引出了我们的第二种方法,数学分析法.
分析梯度
svm loss:
首先回顾一下公式:
Svm Loss: Li=∑j≠yimax(0,wTjxi−wTyixi+Δ))
Total Loss: L=1N∑Li+λ∑∑Wkj2
首先对 Li 求梯度:
∇wyiLi=∑j≠yi1(wTjxi−wTyixi+Δ>0)(−xi)
和
∇wjLi=∑j≠yi1(wTjxi−wTyixi+Δ>0)(xi)
其中1(.)代表如果满足括号内的表达式取1,否则取0.
由于有正则项,所以还要对正则项关于W求导:
∇WR(W)=2λW
由于 λ 不确定,所以 2λ=λ
∇WR(W)=λW
每输入一副图像 xi 迭代的时候, ∇wyi 需要计算类别数-1次,所以 wyi 需要更新类别数-1次, ∇wj 是一个for循环的过程,对于每一个 wj 只更新一次, ∇WR(W) 只需要计算一次,在做cs231n作业的时候就能明白具体的过程了.
Softmax loss:
Softmax Loss: Li=−log(ewTyixi∑kewjxi)
Total Loss: L=1N∑Li
其中 Li 也可以写作:
Li=−wTyixi+log(∑jewjxi)
下面进行求梯度,
if j=yi 则 ∇wj=−xi+xiewTyixi∑jewjxi=(softmax(yi)−1)xi
else 则 ∇wj=xiewTyixi∑jewjxi=softmax(j)xi
其中 softmax(j)=esj∑kesk s 为 wTjxi
在迭代的过程中,可以看出和svm不同, wyi 不需要更新类别数-1次,因为并不在一个求和号里面,所以和 wj 一样只需要更新一次.
梯度检验
数值梯度求到的是近似梯度,因为h不能等于零。分析梯度需要使用微积分,它是计算得到真正的梯度,而且它非常快。但是分析梯度容易出错;这也是为什么在实践中,经常使用分析梯度和数值梯度对比来验证分析梯度。这叫做梯度检验gradien check。
检验的方法就是首先求出分析梯度,然后在当前W下求出数值梯度,然后和分析梯度进行对比,如果误差在一定范围内,则证明分析梯度计算正确.
mini-batch 梯度下降
当训练集比较大时,以计算机所有样本来计算梯度,之后更新一次参数。这样做有点浪费。一个常用的方法是使用训练集一批样本来计算梯度。这个方法之所以也管用,是因为训练集样本是相关的。一小批样本可以看做训练集的近似。
比如有5000个训练样本,规定每一个batch的大小为50,然后迭代n次,每一次随机选取50个样本(可以设置每次选取的都不一样)组成一个batch进行计算梯度和损失,这样能够提高训练速度,也方便进行gpu加速.