Graph Attention Networks(GAT)学习笔记

Graph Attention Networks

论文相关信息

论文链接: https://arxiv.org/abs/1710.10903.
代码链接(keras版本): https://github.com/danielegrattarola/keras-gat.

相关介绍

GCN虽然很强大却也有着诸多局限性：
无法完成inductive任务：无法处理动态图问题，GCN将一整张图作为模型的输入，训练所得模型在其他图结构上的泛化能力差。
对同阶的邻域上分配不同的邻居的权重完全相同：限制了模型对于空间信息的相关性的捕捉能力。
GAT针对GCN缺点所做的改进：
引入attention ：为每个邻居节点分配不同权重，从而关注那些作用比较大的节点，忽视一些作用较小的节点。
泛化能力强：可完成inductive任务，可用子图进行训练，既不需要矩阵运算，也不需要事先知道图结构。

核心思想

注意力机制不外乎计算注意力系数和加权求和这两步

计算注意力系数

向量 hi 就是节点 i 的feature向量
注意力系数 eij 表示节点 j 对于节点 i 的重要性
计算注意力系数之前先用权重W将每个特征转换为可用的表达性更强的特征

Ni 表示节点i的邻居节点集合
系数 α 表示每次卷积时，用来进行加权求和的系数
将以上两个公式结合一下，添加上激活函数leaky ReLU(负倾斜率=0.2)可得以下公式：

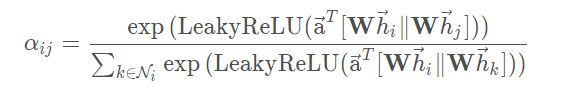
||表示concatenation操作（串联），即将两个张量粘合在一起。举个栗子：将[[1， 2], [3，4]]和[[5, 6], [7, 8]]粘合在一起就是[[1， 2], [3，4]，[5, 6], [7, 8]]。
下图为论文中计算注意力系数的流程示意图：

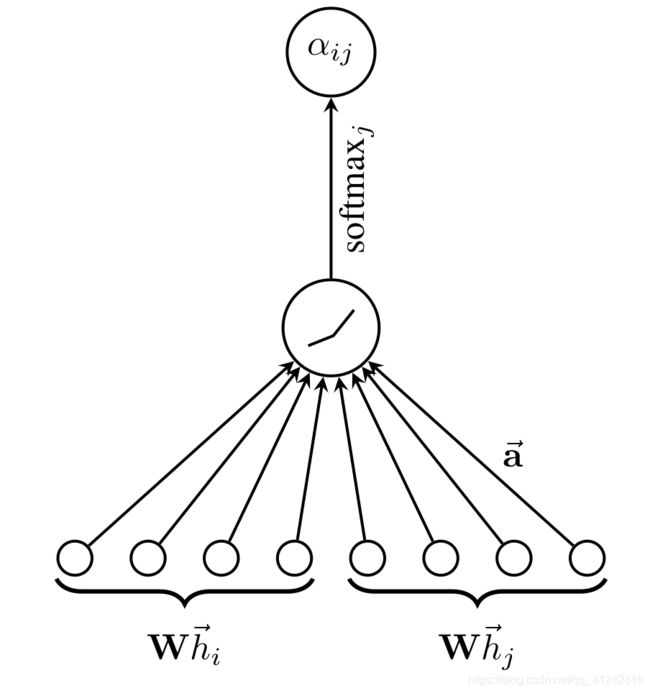
代码实现：

        for head in range(self.attn_heads):
            kernel = self.kernels[head]  # W in the paper (F x F')
            attention_kernel = self.attn_kernels[head]  # Attention kernel a in the paper (2F' x 1)

            # Compute inputs to attention network
            features = K.dot(X, kernel)  # (N x F')

            # Compute feature combinations
            # Note: [[a_1], [a_2]]^T [[Wh_i], [Wh_2]] = [a_1]^T [Wh_i] + [a_2]^T [Wh_j]
            attn_for_self = K.dot(features, attention_kernel[0])    # (N x 1), [a_1]^T [Wh_i]
            attn_for_neighs = K.dot(features, attention_kernel[1])  # (N x 1), [a_2]^T [Wh_j]

            # Attention head a(Wh_i, Wh_j) = a^T [[Wh_i], [Wh_j]]
            dense = attn_for_self + K.transpose(attn_for_neighs)  # (N x N) via broadcasting

            # Add nonlinearty
            dense = LeakyReLU(alpha=0.2)(dense)

            # Mask values before activation (Vaswani et al., 2017)
            mask = -10e9 * (1.0 - A)
            dense += mask

            # Apply softmax to get attention coefficients
            dense = K.softmax(dense)  # (N x N)

从流程示意图和代码中我们可以看出，把一个2F’x1的attention kernel分成两个F’x1的小kernel，attn_for_self负责自注意力，attn_for_neighs负责邻节点注意力。通过用这两个小kernel分别对特征矩阵(就是代码中的features)相乘，就能得到两个Nx1的张量，即自注意力指标和邻注意力指标。假设获得的自注意力指标sa={1, 2, 3, 4, 5}，而获得的邻注意力指标na={a, b, c, d, e}。sa+na.T将其扩充到二维，可得到一张二维表格：

a+1	a+2	a+3	a+4	a+5
b+1	b+2	b+3	b+4	b+5
c+1	c+2	c+3	c+4	c+5
d+1	d+2	d+3	d+4	d+5
e+1	e+2	e+3	e+4	e+5

可见节点3对于节点1的重要性与节点1对于节点3的重要性是不同的，因此该算法应用到有向图上。
self-attention是一种Global graph attention，会将注意力分配到图中所有的节点上，这种做法显然会丢失结构信息。因为基于空间相似假设，一个样本与一定范围内的样本关系较密切。为了解决这一问题，作者使用了一种 masked attention 的方法，对于一个样本来说只利用邻域内的样本计算注意力系数和新的表示，即仅将注意力分配到节点的一阶邻居节点集上。因此作者对注意力矩阵做一下mask进行过滤(即邻接矩阵A中元素为0的位置，将其注意力系数置为负无穷)，再将这个矩阵送入softmax，就可以得到注意力系数矩阵了。

加权求和

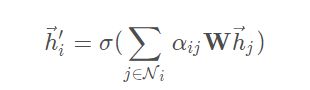
$h_i^{\prime }$代表的是该层图注意力层关于节点i的输出特征
$N_i$是节点i的邻接节点
${\alpha }_{ij}$是之前求得的注意力系数
$\sigma$是激活函数的意思，这里用的激活函数是elu
代码实现：

# Apply dropout to features and attention coefficients
            dropout_attn = Dropout(self.dropout_rate)(dense)  # (N x N)
            dropout_feat = Dropout(self.dropout_rate)(features)  # (N x F')

            # Linear combination with neighbors' features
            node_features = K.dot(dropout_attn, dropout_feat)  # (N x F')

            if self.use_bias:
                node_features = K.bias_add(node_features, self.biases[head])

            # Add output of attention head to final output
            outputs.append(node_features)

        # Aggregate the heads' output according to the reduction method
        if self.attn_heads_reduction == 'concat':
            output = K.concatenate(outputs)  # (N x KF')
        else:
            output = K.mean(K.stack(outputs), axis=0)  # N x F')

        output = self.activation(output)
        return output

代码中没有解释到的就只有attn_heads了，其实这个attn_heads就是论文中的K。
这里作者为了使self-attention 的学习过程更稳定，使用 multi-head attention来扩展注意力机制。下图表示K = 3时的multi-head attention机制示意图。不同的箭头样式表示独立的注意力计算，并且有着独立的注意力系数矩阵。

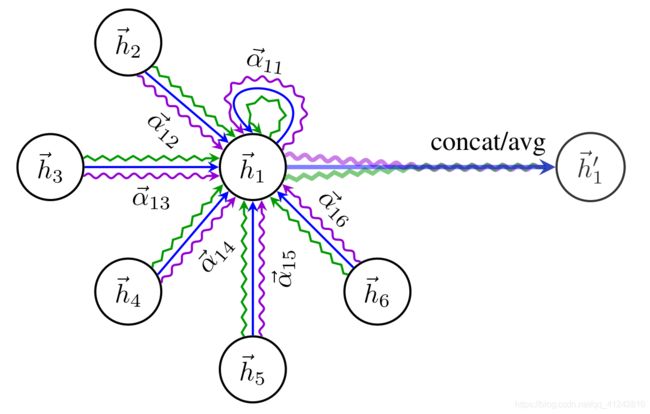
使用K个独立的 attention 机制计算注意力系数，然后他们的特征连(concatednated)在一起，就可以得到如下的输出：

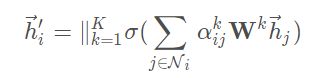
对于最后一个卷积层，如果还是使用multi-head attention机制，那么就不采取连接的方式合并不同的attention机制的结果了，而是采用求平均的方式进行处理，即：

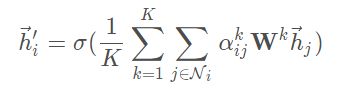
实验和评价

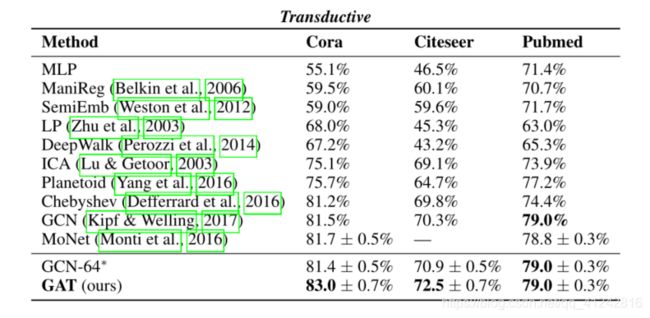
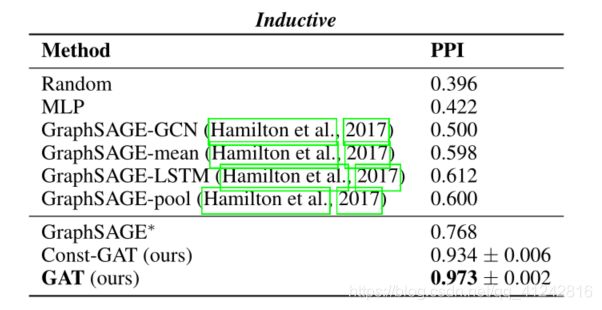
实验分成两部分，transductive learning（半监督学习）和inductive learning（归纳学习）。

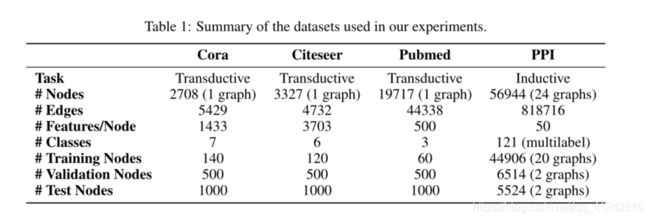
数据集

半监督学习transductive learning

归纳学习inductive learning

和当前工作的对比

计算高效：self-attention层的操作可以在所有的边上并行，输出特征的计算可以在所有顶点上并行。没有耗时的特征值分解。单个GAT的时间复杂度与Kipf & Welling, 2017的GCN差不多。尽管 multi-head 注意力将存储和参数个数变为了K倍，但是单个head的计算完全独立且可以并行化。
鲁棒性更强：和GCN不同，本文的模型可以对同一个 neighborhood的node分配不同的重要性，使得模型的capacity大增。
注意力机制以一种共享的策略应用在图的所有的边上，因此它并不需要在训练之前就需要得到整个图结构或是所有的顶点的特征（很多之前的方法的缺陷）。因此GAT 也是一种局部模型。也就是说，在使用 GAT 时，无需访问整个图，而只需要访问所关注节点的邻节点即可，解决了之前提出的基于谱的方法的问题。因此这个方法有两个影响：图不需要是无向的，可以处理有向图（若j→i不存在，仅需忽略${\alpha }_{ij}$即可）；可以直接应用到 inductive learning：包括在训练过程中在完全未见过的图上评估模型的任务上。
2017年Hamilton提出的归纳学习方法（GraphSAGE）为每一个节点都抽取一个固定尺寸的邻居大小，为了计算的时候输入是一致的（指的应该是计算的时候处理邻居的模式是固定的，不好改变，因此每次都抽样出固定数量的邻居节点参与计算），这样，在计算的时候就不是所有的邻居节点都能参与其中。此外，Hamilton的这个模型在使用一些基于LSTM的方法的时候能得到最好的结果，这样就是假设了每个节点的邻居节点一直存在着一个顺序，使得这些节点成为一个序列。但是本文提出的方法就没有这个问题，每次都可以将邻居中所有的节点都考虑进来，而且不需要事先假定一个邻居节点的顺序。

参考：https://blog.csdn.net/leviopku/article/details/104622560?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522161879411116780274172516%2522%252C%2522scm%2522%253A%252220140713.130102334…%2522%257D&request_id=161879411116780274172516&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2_alltop_positive~default-1-104622560.first_rank_v2_pc_rank_v29&utm_term=gat