机器学习--KNN算法
目录
一、KNN算法
1、KNN算法是什么?
2.KNN算法的理解
二、KNN算法的关键
1.K的取值
2.距离的测算
三、算法实现-通过体重身高预测性别
一、KNN算法
1、KNN算法是什么?
KNN(K- Nearest Neighbor)法即K最邻近法,最初由 Cover和Hart于1968年提出,是最简单的机器学习算法之一,属于有监督学习中的分类算法。算法思路简单直观:分类问题:如果一个样本在特征空间中的K个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。KNN是分类算法。
2.KNN算法的理解
即对于一个需要预测的输入向量x,我们只需要在训练数据集中寻找k个与向量x最近的向量的集合,然后把x的类别预测为这k个样本中类别数最多的那一类。
二、KNN算法的关键
1.K的取值
由于k值较大,预测标签比较稳定,但可能过平滑;k值较小,预测的标签比较容易受到样本的影响。往往K值较小且是奇数,避免产生占比相同
2.距离的测算
KNN算法通常的距离测算方式为欧式距离和曼哈顿距离,相比之下欧氏距离会更常用
欧式距离公式:
曼哈顿距离公式:
三、算法实现-通过体重身高预测性别
数据格式:身高,体重,性别(标签)
总计100条
读取文件画图,通过图形化分析数据(数据分享:链接https://pan.baidu.com/s/1Ld7ihLNT5AkfGDFEBxAP6A
提取码:1234):
filname = 'D:/learn/three first/machine learning/Data.txt'
datingDateMat, datingLabels = file2maxtrix(filname)
print('datingDateMat: {}'.format(datingDateMat))
#对标签数字化
labels=datingLabels
for i in range(0, len(datingLabels)):
print(i)
if datingLabels[i]=='男':
labels[i]=1
else:
labels[i]=0
print(labels[i])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(datingDateMat[:,0], datingDateMat[:,1], c=labels)
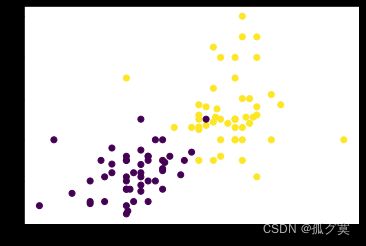
plt.show()如图:
KNN算法
def classify(trainData,testData,labels,k):
tempData = np.tile(testData,(trainData.shape[0],1))
#欧式距离
tempData=((tempData-trainData)**2).sum(axis=1)**0.5
sortData=tempData.argsort()
count={}
for i in range(k):
vote=labels[sortData[i]]
count[vote]=count.get(vote,0)+1
sortData=sorted(count.items(),key=operator.itemgetter(1),reverse=1)
return sortData[0][0]文件读取
def file2maxtrix(filename):
fr = open(filename,'r',encoding='utf-8-sig')
arrayOLines = fr.readlines()
numberOfLines = len(arrayOLines)
returnMax = np.zeros((numberOfLines, 2))
classLabelVector = []
index = 0
for line in arrayOLines:
line = line.strip()
listFromLine = line.split(' ')
returnMax[index,:] = listFromLine[0:2] #前二列是训练样本数据
classLabelVector.append(listFromLine[-1]) #最后一列是标签集合
index += 1
return returnMax, classLabelVector测试代码
def datingClassTest():
hoRatio=0.9
datingDataMat,datingLabels=file2maxtrix('D:/learn/three first/machine learning/Data.txt')
m=datingDataMat.shape[0]
numTestVecs=int(m*hoRatio)
goodK=1
oldErrorRate=1.0
for k in range(1,numTestVecs):
print(k)
errorCount=0.0
for i in range(m-numTestVecs):
classifierResult=classify(datingDataMat[0:numTestVecs,:],datingDataMat[numTestVecs+i,:],datingLabels[0:numTestVecs],k)
print("the classifier came back with: %s, the real answer is: %s" % (classifierResult, datingLabels[numTestVecs+i]))
if(classifierResult!=datingLabels[numTestVecs+i]):
errorCount+=1.0
errorRate= errorCount/float(m-numTestVecs)
if errorRate运行结果
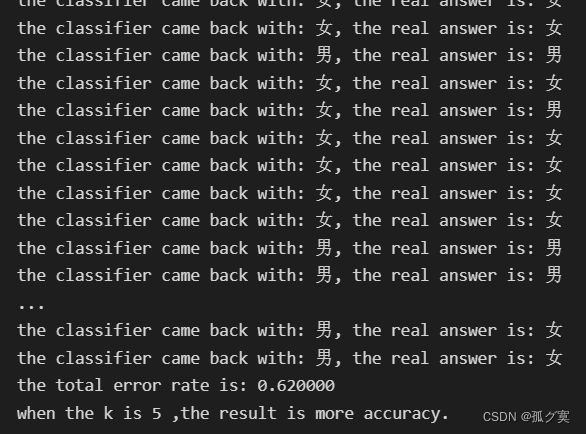
当取数据50%作为训练样本 ,K=5时错误率更小
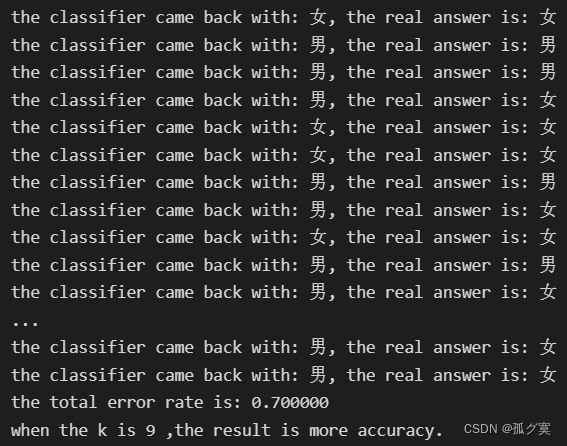
当取数据70%作为训练样本 ,K=9时错误率更小
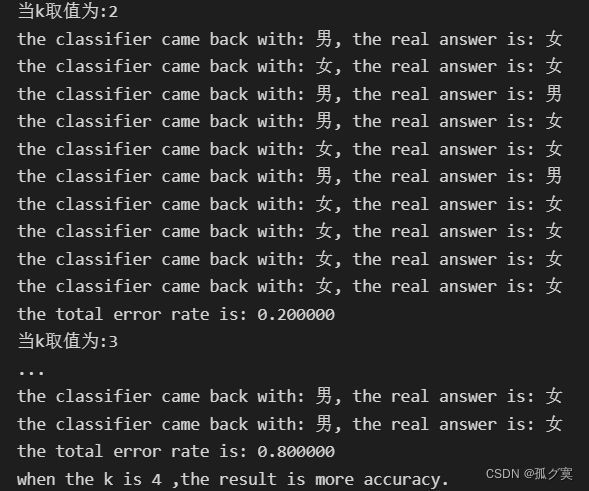
当取数据90%作为训练样本 ,K=4时错误率更小
实验结果分析:K的最佳值会受到测试数据的多少影响,当测试样本过少,则容易造成过拟合;当测试样本过多,这k的值可能过少。