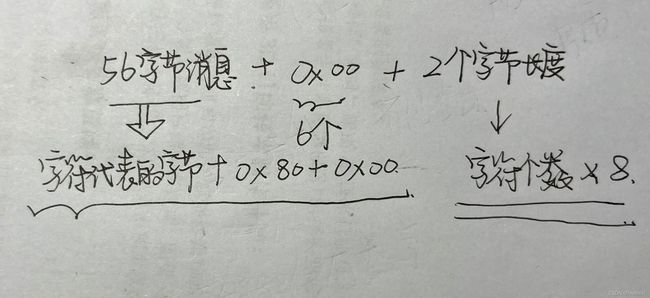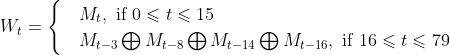SHA算法的C++实现

目录

消息填充

消息分割与扩展

SHA的四轮运算

---

本来不太理解SHA算法怎么存储、运算，查阅资料后发现，SHA-1算法中不会出现对单个比特位的操作，都是以字节/四个字节为单位的，所以我调用bitset类更方便的存储运算。

#define CSLeft(x,n) (((x)<<(n))|((x)>>(32-(n))))
#define CSRight(x,n) (((x)>>(n))|((x)<<(32-(n))))
#define trans(x) (x.to_ulong())

消息填充

sha-1算法处理：输入以512比特数据块为处理单位。

已知公式：  (L是原始消息长度，1是填充位1，k是填充0的个数) 

其余64位为原始L位消息长度的二进制表示

我首先定义了 typedef bitset<8> byte; 来表示一个比特8位二进制。原因是我的输入的消息为字符串plain，按asc-128位的存储方式，一个字符需要8位二进制来存储，即一个字符一个byte，输入时最多不超过56个字节。

56*8=448比特，所以我们最多需要两个比特来存储长度（一个字节最多表示255位长度）。

//消息填充
void MessFill(string plain,int len,byte m[]){
	char temp;
	//存入每一个字符的asc码
	for(int i=0;i= 255){
		m[62] = numlen-255;
		m[63] = 255;
	}else{
		m[63] = numlen;
	}
	for(int i=0;i<64;i++){
		cout << trans(m[i]) << "\t";
	}
	cout << endl;
}

消息分割与扩展

512位的明文被划分为16个明文分组，每组32位。然后将16份子明文分组扩展为80份。

我定义了 typedef bitset<32> word;以此代表32位比特的分组。

//消息分割与扩展
void MessDivi(byte m[],word w[]){
	int t;
	for(t=0;t<16;t++){
		w[t] |= CSLeft(trans(m[4*t]),24);
		w[t] |= CSLeft(trans(m[4*t+1]),16);
		w[t] |= CSLeft(trans(m[4*t+2]),8);
		w[t] |= trans(m[4*t+3]);
	}
	for(t=16;t<80;t++){
		w[t] = CSLeft(w[t-3]^w[t-8]^w[t-14]^w[t-16],1);
	}
	cout << endl;
}

SHA的四轮运算

（1）首先设置初始散列值

word A = 0x67452301;
word B = 0xEFCDAB89;
word C = 0x98BADCFE;
word D = 0x10325476;
word E = 0xC3D2E1F0;

（2）运算准备

在bitset类中，是未定义+-*等运算法则的，我经过尝试发现sha算法实现的过程中需要很多的+运算，因此重载了运算符+。

word operator+(word a,word b){
	word c;
	int t=0;//进位
	for(int i=0;i<32;i++){
		if(a[i]==0 && b[i]==0){
			if(t == 0){
				c[i] = 0;
			}else{
				c[i] = 1;
			}
			t = 0;
		}else if(a[i]==1 && b[i]==1){
			if(t == 0){
				c[i] = 0;
			}else{
				c[i] = 1;
			}
			t = 1;
		}else{
			if(t == 0){
				c[i] = 1;
			}else{
				c[i] = 0;
			}
		}
	}
	return c;
}

其次，在SHA四轮运算中，每一轮20个步骤，一共执行80步。这80步中，每一步都相同，但每一步使用的Kt，Ft不同，Kt，Ft根据轮数划分成四个阶段，所以SHA的运算分为四轮。

 

 因此，准备代码如下：

//ft、kt
word ft(word b,word c,word d,int t){
	if(t>=0 && t<=19){
		return ((b&c)|((~b)&d));
	}else if(t>=20 && t<=39){
		return (b^c^d);
	}else if(t>=40 && t<=59){
		return ((b&c)|(b&d)|(c&d));
	}else if(t>=60 && t<=79){
		return (b^c^d);
	}
}
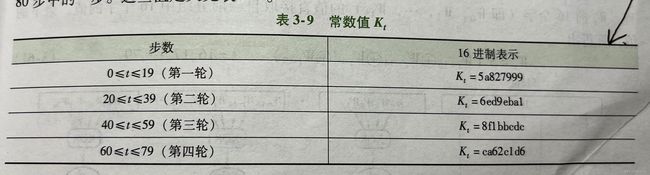
word kt(int t){
	if(t>=0 && t<=19){
		return 0x5A827999;
	}else if(t>=20 && t<=39){
		return 0x6ED9EBA1;
	}else if(t>=40 && t<=59){
		return 0x8F1BBCDC;
	}else if(t>=60 && t<=79){
		return 0xCA62C1D6;
	}
}

（3）SHA算法的整体流程

整个流程就很简单啦，不要忘了最后还要加上原始变量。A,B,C,D,E即为160位杂凑码。

void SHA(string plain,int len){
	byte m[64];
	MessFill(plain,len,m);
	word w[80];
	MessDivi(m,w);
	word temp,A1=A,B1=B,C1=C,D1=D,E1=E;
	for(int i=0;i<80;i++){
		temp = CSLeft(A1,5) + ft(B1,C1,D1,i) + E1 + w[i] + kt(i);
		E1 = D1;
		D1 = C1;
		C1 = CSLeft(B1,30);
		B1 = A1;
		A1 = temp;
	}
	A = A1+A;
	B = B1+B;
	C = C1+C;
	D = D1+D;
	E = E1+E;
}