[Python系列-16]:人工智能 - 数学基础 -6- 常见数学函数、激活函数大全
作者主页(文火冰糖的硅基工坊):https://blog.csdn.net/HiWangWenBing
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/119322837
目录
第1部分 函数概述
1.1 函数的定义
1.2 计算机函数与数学函数的异同
1.3 数学函数在深度学习中应用
第2章 常见的初等数学函数
2.1 常数函数
2.2 幂函数
2.3 指数函数
2.4 对数函数
2.5 三角函数
第3章 多项式函数
3.1 零次多项式:常数函数
3.1 一次多项式
3.2 二次多项式
3.3 三次多项式
3.4 三次多项式函数
第4章 深度学习-神经元的激活函数
4.0 激活函数的作用
4.1 Sigmoid函数
4.2 tanh函数函数
4.3 Relu函数
4.4 ELU (Exponential Linear Units) 函数
第5章 高等函数-多元函数
5.1 多元函数概述
5.2 一元一次函数: y = f(x)
5.2 二元一次函数: y = f(x1, x2)
5.3 三元一次函数: y = f(x1, x2, x3)
第1部分 函数概述
1.1 函数的定义
(1)计算机领域
函数是指一段可以直接被另一段程序或代码引用的程序或代码。也叫做子程序。
(2)数学领域:
函数是一种关系,是一种映射规则,这种关系使一个集合里的每一个元素对应到另一个(可能相同的)集合里的唯一元素的规则。
1.2 计算机函数与数学函数的异同
(1)相同点
- 模型相同:输入》处理 =》输出
- 都是多输入
(2)不同点
- 内在的处理方法不同
计算领域:是逻辑处理
数学领域:是映射规则
- 输出不同:计算机领域是可以任意个输出变量,数学领域是单一输出变量。
- 工程师的角色不同
1.3 数学函数在深度学习中应用
(1)神经网络的神经元
神经网络的神经元就是一个函数,也就是说,神经网络就是N个输出的N个“函数”。
(2)误差或损失函数loss
误差或损失函数loss就是用函数来表示的,loss函数的输出值y,是神经网络的各个神经元函数的系数的函数。
第2章 常见的初等数学函数
2.1 常数函数
在数学中,常数函数(也称常值函数)是指值不发生改变(即是常数)的函数
2.2 幂函数
2.3 指数函数
指数函数是重要的基本初等函数之一。一般地,y=a^x函数(a为常数且以a>0,a≠1)叫做指数函数,函数的定义域是 R
2.4 对数函数
对数函数是以幂(真数)为自变量,指数为因变量,底数为常量的函数。
![]()
2.5 三角函数
三角函数是基本初等函数之一,是以角度(数学上最常用弧度制,下同)为自变量,角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。
第3章 多项式函数
多项式函数,是数学概念,形如f(x)=an·x^n+an-1·x^(n-1)+…+a2·x^2+a1·x+a0的函数,叫做多项式函数,它是由常数与自变量x经过有限次乘法与加法运算得到的。
很显然,多项式函数是多个幂函数组合而成的函数。
3.1 零次多项式:常数函数
y = a0,形如
3.1 一次多项式
形如 y=kx+b (k为任意不为0的常数,b为任意常数)的函数叫做一次函数(linear function),也称线性函数,或称为直线函数。
其图像在平面直角坐标系中可以用一条直线表示,当一次函数中的一个变量的值确定时,可以用一元一次方程确定另一个变量的值。
备注:
人工神经元的输入分支:1个一次多项式函数(或直线)
人工神经元整体就是由:N个一次多项式函数的累计和 与 激活函数串联。
人工神经网络就由无数个神经元串联而成 (“一次多项式函数 + 激活函数”)
Y = (W1*X1 + W2*X2 + ..... Wn*Xn) - B。
其中:
(1)神经元输入分支
Wi:是直线的系数;
Xi:为自变量
Yi:为因变量, Yi = Wi * Xi + Bi
Bi:为系数
(2)神经元综合效果:
B:是所有系数Bi的累计和。
Y: 是所有因变量Yi的累计和; Y = (W1*x1 + W2*X2 + ..... Wn*Xn) - B。
3.2 二次多项式
(1)二次多项式
一般地,形如y=ax^2+bx+c的函数叫做二次函数(quadratic function)。
二次函数是自变量的最高次数为二次的多项式函数。
(2)二次多项式在深度学习中的应用
二次多项式被广泛应用于就损失函数loss函数。
loss函数的本质是:实际的数据点到拟合线(线段)的距离(这个距离称为误差)的平方之和。
因此 loss函数本质是一个二次函数,是N元的二次函数,是由N个一元二次函数组合而成。
N元的二次函数在高等函数中再进一步阐述。
3.3 三次多项式
最高次数项为3的函数,形如y=ax³+bx²+cx+d(a,b,c,d为常数,且a不等于0)的函数叫做三次函数(cubic function)。 三次函数的图象是一条曲线——回归式抛物线(不同于普通抛物线)。
3.4 三次多项式函数
形如y=ax4+bx3+cx2+dx+e(a≠0,b,c,d,e为常数)的函数叫做四次函数。四次函数的图像成一般W形。
第4章 深度学习-神经元的激活函数
4.0 激活函数的作用
(1)限制输出
神经元的一次函数,输入与输出是线性关系,因此输出是无穷大。
为了限制神经元的输出信号的幅度,需要通过某种激活函数对输出信号进行限制。
(2)提高门槛
神经元的一次函数,输入与输出是线性关系,因此输出是任意值。
生物神经元只有在输入信号得到一定的门限时,才会有输出。
为了模拟生物神经元的门槛功能,需要通过某种激活函数来对输出信号的最低值进行限制。
4.1 Sigmoid函数
(1)公式
(2)图形
(3)特点
- 无论线性函数的输出是多大,该激活函数把输出限制在(0,1)之间.
- 如果线性函数的输出值为负无穷时,输出为0;
- 如果线性函数的输出值为正无穷时,输出为1.
- 如果线性函数的输出值为0时,输出中值为0.5.
- 导函数平滑
4.2 tanh函数函数
(1)公式
(2)图形
![]()
(3)特点
- 无论线性函数的输出是多大,该激活函数把输出限制在(-1,1)之间.
- 如果线性函数的输出值为负无穷时,输出为-1;
- 如果线性函数的输出值为正无穷时,输出为+1.
- 如果线性函数的输出值为0时,输出中值为0.
- 导函数平滑
4.3 Relu函数
(1)公式
(2)图形
![]()
(3)特点
- 无论线性函数的输出是多大,该激活函数把输出限制在(0,+无穷)之间,即把所有的负数都映射成0.
- 如果线性函数的输出值为负数时,输出为0;限制负数幅度映射为0.
- 如果线性函数的输出值为正数时,输出等于输入y = x,不限制正数的映射幅度。
- 如果线性函数的输出值为0时,输出为0.
- 导函数不平滑
4.4 ELU (Exponential Linear Units) 函数
(1)数学公式
(2)图形表示
![]()
(3)特点
- 当x<0时,采用指数映射,限制负数的幅度。
- 当x>0时,采用线性映射,不限制正数的幅度。
- 当x=0是,映射值为0.
- 导函数不平滑
第5章 高等函数-多元函数
5.1 多元函数概述
5.2 一元一次函数: y = f(x)
5.2 二元一次函数: y = f(x1, x2)
5.3 三元一次函数: y = f(x1, x2, x3)
作者主页(文火冰糖的硅基工坊):https://blog.csdn.net/HiWangWenBing
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/119322837
![[Python系列-16]:人工智能 - 数学基础 -6- 常见数学函数、激活函数大全_第1张图片](http://img.e-com-net.com/image/info8/7ffe68f6d79740c9b34f232de7659b3c.jpg)
![[Python系列-16]:人工智能 - 数学基础 -6- 常见数学函数、激活函数大全_第2张图片](http://img.e-com-net.com/image/info8/db2998e7568e40b7a3490752c1d7cfae.jpg)
![[Python系列-16]:人工智能 - 数学基础 -6- 常见数学函数、激活函数大全_第3张图片](http://img.e-com-net.com/image/info8/aecedc752efe4f03922e00caf3d4b3ec.jpg)
![[Python系列-16]:人工智能 - 数学基础 -6- 常见数学函数、激活函数大全_第4张图片](http://img.e-com-net.com/image/info8/338699068cf2430cbd4e12619dfa5b44.png)
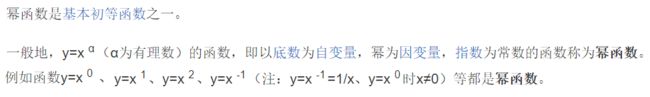
![[Python系列-16]:人工智能 - 数学基础 -6- 常见数学函数、激活函数大全_第5张图片](http://img.e-com-net.com/image/info8/2d69aec40aba478799947136f53e8d10.jpg)
![[Python系列-16]:人工智能 - 数学基础 -6- 常见数学函数、激活函数大全_第6张图片](http://img.e-com-net.com/image/info8/6d3604dd141a4f0fbb9ef2166479bee8.jpg)
![[Python系列-16]:人工智能 - 数学基础 -6- 常见数学函数、激活函数大全_第7张图片](http://img.e-com-net.com/image/info8/c77e0c2ab9bb4af492402ee6e00af559.jpg)
![[Python系列-16]:人工智能 - 数学基础 -6- 常见数学函数、激活函数大全_第8张图片](http://img.e-com-net.com/image/info8/1717d7718fb74b25b372337360842ffd.jpg)
![[Python系列-16]:人工智能 - 数学基础 -6- 常见数学函数、激活函数大全_第9张图片](http://img.e-com-net.com/image/info8/86178b6f06164b05b5b42129892230ee.jpg)
![[Python系列-16]:人工智能 - 数学基础 -6- 常见数学函数、激活函数大全_第11张图片](http://img.e-com-net.com/image/info8/dd3a85d6856c48cc8ad43468e2b0d5d2.jpg)
![[Python系列-16]:人工智能 - 数学基础 -6- 常见数学函数、激活函数大全_第12张图片](http://img.e-com-net.com/image/info8/584e06b8b4e74c3ab588e9b3805a6287.jpg)
![[Python系列-16]:人工智能 - 数学基础 -6- 常见数学函数、激活函数大全_第13张图片](http://img.e-com-net.com/image/info8/0e02845d1ba449c79c07fa4ba6f63ced.jpg)
![[Python系列-16]:人工智能 - 数学基础 -6- 常见数学函数、激活函数大全_第14张图片](http://img.e-com-net.com/image/info8/f0a2823cdd364c3fb2d953b5688a426a.jpg)
![[Python系列-16]:人工智能 - 数学基础 -6- 常见数学函数、激活函数大全_第15张图片](http://img.e-com-net.com/image/info8/7dd18a8f5dd9493e87381f3f80447e76.jpg)
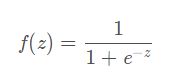
![[Python系列-16]:人工智能 - 数学基础 -6- 常见数学函数、激活函数大全_第16张图片](http://img.e-com-net.com/image/info8/3f0e80df8c7945f59ae48a662b8ce81c.jpg)
![[Python系列-16]:人工智能 - 数学基础 -6- 常见数学函数、激活函数大全_第17张图片](http://img.e-com-net.com/image/info8/40fe7e5d8d88434592156a440677d810.jpg)
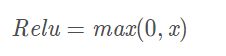
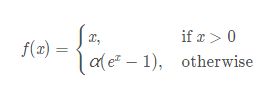
![[Python系列-16]:人工智能 - 数学基础 -6- 常见数学函数、激活函数大全_第18张图片](http://img.e-com-net.com/image/info8/685ddbe340a1429aaf4592677dd0cc32.jpg)
![[Python系列-16]:人工智能 - 数学基础 -6- 常见数学函数、激活函数大全_第19张图片](http://img.e-com-net.com/image/info8/39790bff76284231b3c33c7d84e319a0.jpg)
![[Python系列-16]:人工智能 - 数学基础 -6- 常见数学函数、激活函数大全_第20张图片](http://img.e-com-net.com/image/info8/8ffd01c5df3e4139b55369bb5f8af8c7.gif)