人工智能导论 第二章 搜索技术

2.1 搜索的基本概念

搜索：一种求解问题的一般方法

问题求解的基本方法：搜索法、归约法、归结法、推理法及产生式

基本问题：

1、是否一定能找到一个解

2、找到的是否是最佳解

3、时间和空间复杂度

4、是否会终止运行or死循环

主要过程：

1、从初始或目的状态出发，并将其作为当前状态

2、扫描操作算子集，将适用当前状态的一些操作算子作用于当前状态而得到新的状态，并建立指向父节点的指针

3、检查所生成的新状态是否满足结束状态。若满足，反向得出解答路径；否则将新状态定义为当前状态返回2

概念术语

搜索方向

（1）数据驱动：初始状态出发正向搜索

（2）目的驱动：从目的状态出发逆向搜索

（3）双向搜索 找到汇合点

盲目搜索与启发式搜索

（1）盲目搜索：不针对特定问题任何有关信息，按照固定步骤搜索

（2）启发式搜索：考虑特定问题可应用的知识，动态确定算子，优先选择合适算子，减少步骤

状态

表示系统状态、事实等叙述性知识的一组变量或数组

操作

表示引起状态变化的过程型知识的一组关系或函数

2.2 状态空间的搜索策略

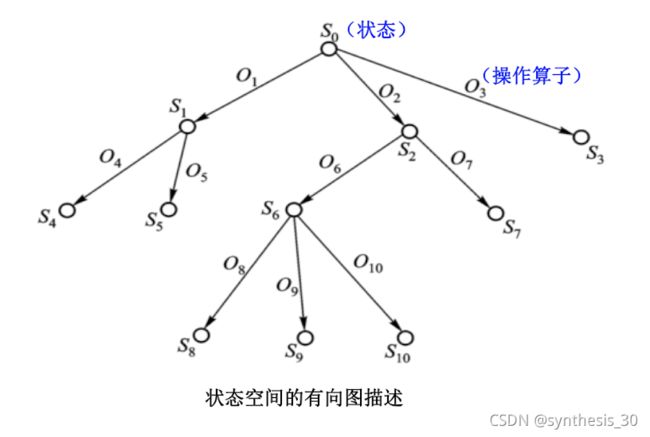
状态空间：利用状态变量和操作符号，标识系统或问题的有关知识的符号体系，三元组（S、F、G）

S：状态集合 F：操作算子的集合 G：目的状态集合

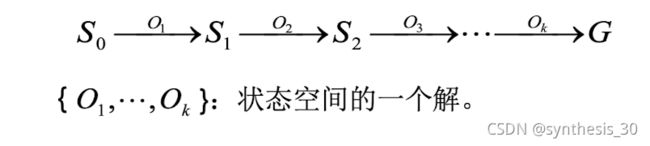
求解路径

从S0到G结点的路径，状态空间的一个解是一个有限的操作算子序列

 表示方法：图描述

八数码问题的图描述

TSP问题的图描述 

2.3 盲目搜索

回溯策略

从初始状态出发不停试探路径，直到到达目的或“不可解节点”。若遇到不可解节点就回溯到路径中最近的父节点上，查看该节点是否还有其他子节点未被扩展。

算法：

1、PS表：保存当前搜索路径上的状态，如果找到目的，PS就是解路径上的状态有序集

2、NPS表：新的路径状态表，包含等待搜索的状态，后裔状态还未被搜索到

3、NSS表：不可解状态集，列出找不到接替路径的状态。如果在搜索中扩展出他的元素，可立即排除

图搜索算法（DFS BFS 最好优先搜索）的回溯思想

（1）用NPS使算法可以回归到任意状态

（2）用NSS避免算法重新搜索无解路经

（3）PS表中记录当前搜索路径状态，满足目的时可以将其作为结果返回

（4）为避免死循环，需要对子状态及性能检查，看是否在3张表中

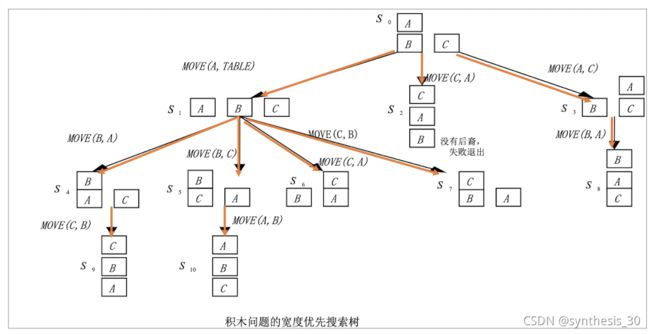
广度优先搜索策略

例题：机器人积木动作序列问题

算子MOVE（X，Y）的先决条件：

1、被搬动积木顶必为空

2、若Y是积木，Y顶部也必须为空

3、同状态下操作算子运用次数不得多于1次

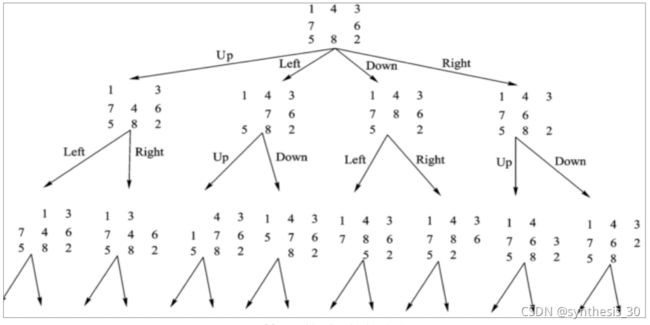
深度优先搜索策略

深度优先搜索中，当搜索到某一状态，其所有子状态及子状态的后裔状态必须先于该状态的兄弟状态被搜索。并且为了保证找到解，应选择合适的深度限制或不断加大深度限制值，反复搜索。

深度优先搜索并不能保证第一次搜索到某个状态时的路径是到这个状态的最短路径，如果算法多次搜索到同一个状态时应当保留最短路径

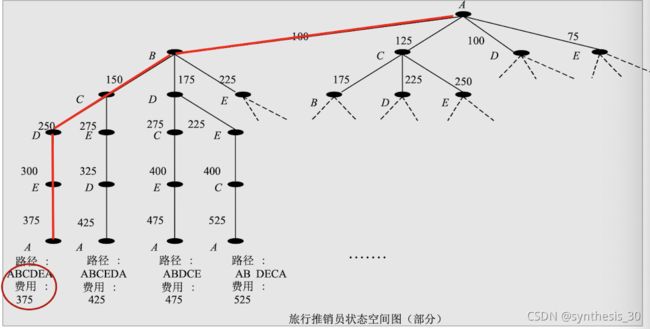
盲目搜索——代价树搜索 

代价树搜索：用于寻找最小代价路径问题，是推广版的BFS（如果权值都一致的话就是BFS）

比较图搜索与树搜索：

最短路径的图搜索：搜索算法认为一个状态只能对应搜索图中的一个节点

最短路径的树搜索 ：同一个状态可以多次出现在树中，相同状态可以同时出现在搜索中代表不同节点

实际操作中可以从搜索树构造搜索图搜索算法，从边缘集合中取出那些会导致搜索出现重复状态的节点。

搜索图是动机的角度，搜索树是实现的角度。

例题：卒子穿阵问题

2.4 启发式图搜索

启发式策略

启发：关于发现和发明操作算子及搜索方法的研究

在状态空间搜索中，启发式被定义成一系列操作算子，并能从状态空间中选择最有希望到达问题解的路径。

启发式策略：利用问题相关的启发信息进行搜索

运用启发策略的两种基本情况

1、一个问题由于在问题陈述和数据获取方面的模糊性，可能使它没有确定解

2、虽有可能有确定解，但是状态空间特别大，生成扩展的状态数会随搜索深度指数级增长

启发信息和估价函数

求解问题中利用的大多是非完备的启发信息

1、求解问题系统不能知道与实际问题有关的全部信息，无法知道所有状态空间，无法用一套算法求解所有问题

2、虽然理论上存在求解算法，但工程实践中不是效率太低就是无法实现

启发信息分类

1、陈述性 2、过程性

3、控制性（没有任何控制性知识作为搜索依据，所以每一步都是随意的；有充分的控制知识作为依据，因而搜索的每一步选择都是正确的）

估价函数：估计代搜索节点的有希望程度，并依次给它们拍定次序

估价函数f（n）从初始节点经过n节点到达目的节点的路径的最小代价估计值f=g+h（g越大先用宽度优先，h越大表示启发能力越强）

总结：利用知识来引导搜索，减少搜索范围，降低问题复杂度

启发信息的强度可以分为：强：降低搜索工作量，可能导致找不到最优解

弱：导致工作量加大，极限情况下可以盲目搜索，但可能找到最优解

引入启发知识，在保证找到最优解的情况下尽可能缩小搜索范围，提高搜索效率

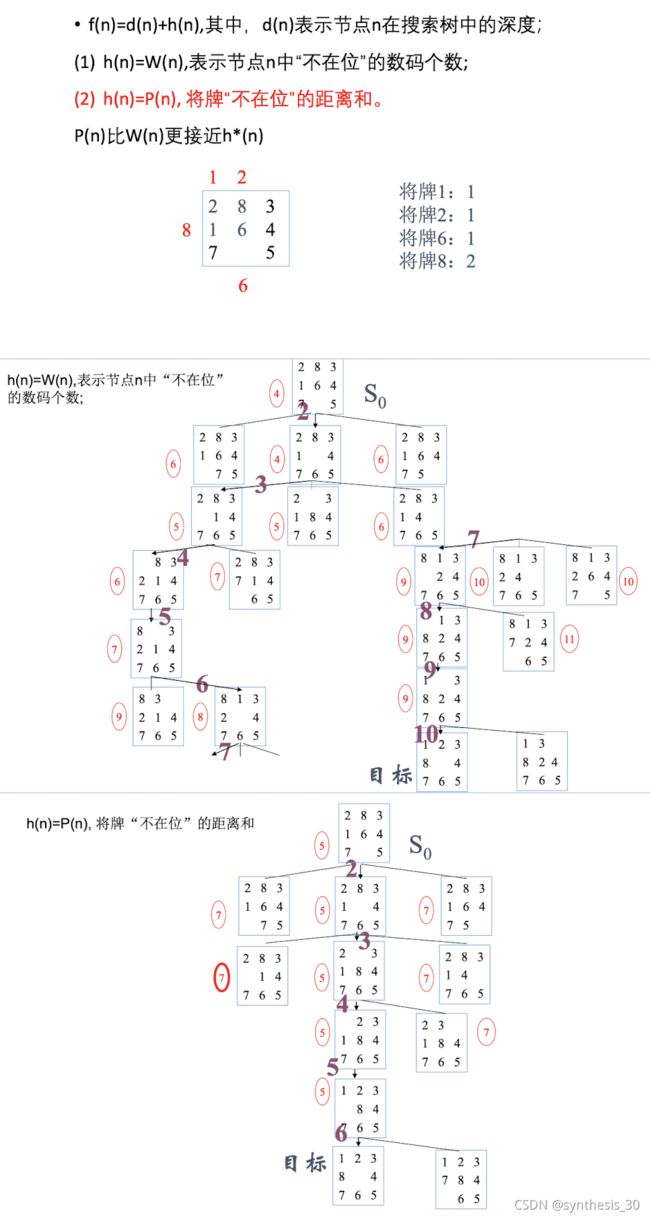
例题：八数码的估价函数

A搜索算法

启发式图搜索算法的基本特点：寻找并设计一个与问题相关的h（n）及构出f（n）=g+h，然后以f（n）的大小来排列待扩展状态的次序，每次选f值最小者进行

open表：保留所有已生成而未扩展的状态

closed表：记录已扩展过的状态

进入open表的状态是根据其估值的大小插入到表中合适的位置，每次从表中优先取出启发估价函数值最小的状态进行扩展。

每次重复时，A搜索算法从open表中取出第一个状态。如果该状态满足目标条件，则算法返回到该状态的搜索路径。

如果open表的第一个状态非目的状态，则算法通过一系列操作算子进行相应操作来产生其子状态。若某子状态在open&closed表中出现过，即该状态再一次被发现时 ，通过刷新祖先状态的历史记录，使算法可能找到更短路径。

A搜索算法接着open表中每个状态的估价函数值，按照值大小重新排序，将值最小的状态放在表头，使其第一个被扩展。

例题：利用A搜索算法求解八数码问题的搜索树，估价函数定义为f=d+w

d：为状态深度，每步代价为单位代价。w：以“不在位”的将牌数作为启发信息的量度。

 （A&A*搜索树）

A*搜索算法及其特性分析

若某一问题有解，A*一定能搜索到解且一定能得到最优解。

A算法没有对估价函数f（n）作任何限制，实际上估价函数对搜索过程也十分重要

A*就是对估价函数加上一些限制后得到的一种启发式搜索算法

可容性：启发函数不会高估从节点n到终止节点所应付出的代价

一致性：三角不等式h(n)<=c(n,a,n')+h(n') ，h（n）是从节点n到目标节点Gn所形成的具有最小开销代价的路径。

2.5 对抗搜索

也称博弈搜索，在竞争环境中智能体之间通过竞争实现相反的利益，一方最大化一方最小化

常见对抗搜索算法：

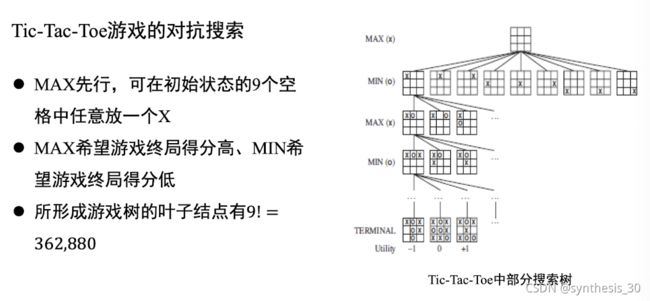
最小最大搜索：在对抗搜索中最为基本的一种让玩家来计算最优策略的方法

Alpha-Beta剪枝搜索：对最小最大搜索进行改进的算法，可在搜索中剪除不需要的分支节点，且不影响搜索结果。

蒙特卡洛树搜索：通过采样而非穷举的方法来实现搜索。

特点：目前主要讨论在确定的、全剧可观察的、竞争对手轮流行动，零和游戏下的对抗搜索

两人对决游戏可以如下形式化描述，转化为对抗搜索问题

零和博弈：损人利己 双赢博弈：利己不损人

MiniMax算法 

给定一个游戏搜索树，minimax算法通过每个节点的minimax值来决定最优策略。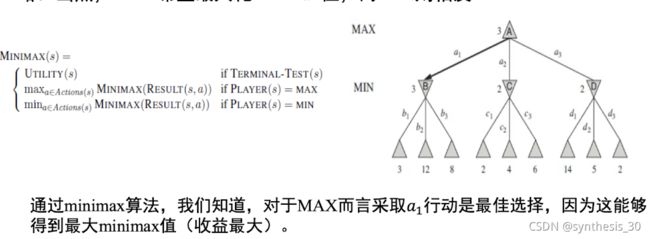

优点：简单有效；对手尽力而为时可返回最优结果

缺点：搜索树太大时，无法在有效时间内返回结果

改进：alpha-beta pruning减少节点；对节点进行采样而非逐一

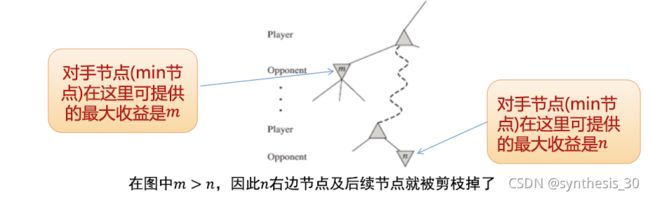
Alpha-Beta剪枝搜索

优化minimax，减少所搜索的搜索树节点数。所得结论与minimax结论相同，但剪去了不影响最终结果的分支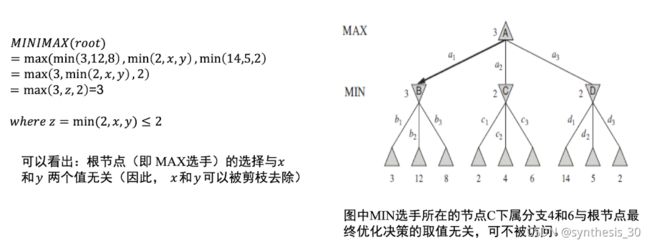 

 

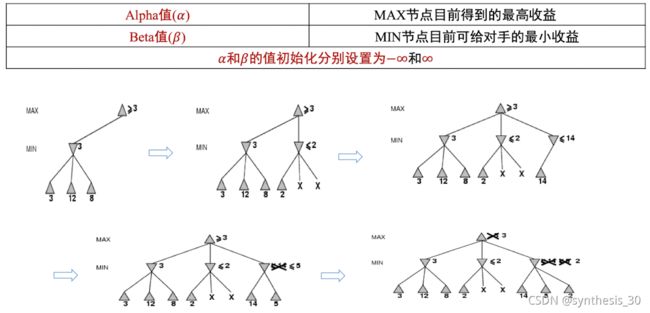
如何利用Alpha-Beta剪枝？

Alpha（a）：

玩家MAX（根结点）目前得到的最高收益；假设n是MIN节点，如果n的一个后续节点可提供的收益小于a，则n及其后续节点都可以剪掉

Beta（b）：

玩家MIN目前给对手的最小收益；假设n是MAX节点，如果n的一个后续节点提供收益大于b，则

及其后的节点都可以减掉

a、b初始化为+∞、-∞

 相当于：a是可能解法的最大上界，b是可能解法的最小下界。若N是可能解法路径中的一个节点，其产生的收益一定在【a，b】区间内

性质：剪枝本身不影响算法输出结果；节点先后次序会影响剪枝效率；最小时间复杂度O（b^(m/2)）,minimax algorithm: O(b^m) 

2.6 蒙特卡洛树搜索

蒙特卡洛规划（Monte-Carlo Planning）

单一状态蒙特卡洛规划：多臂赌博机

单一状态，k种行动（k个摇臂）

每次随机采样形式采取行动a，好比随机拉动第k个赌博机的摇臂，得到R（s，ak）的回报

问题：下一次需要拉动哪个臂膀才能获得最大回报呢

多臂赌博机问题

一种序列决策问题，需要在利用和探索之间保持平衡

利用：保证在过去决策中得到最佳回报

探索：寄希望在未来能够得到更大回报

悔值函数：在第t次对赌博机操作时，设知道哪个赌博机能够给出最大奖赏，则将得到的最大奖赏减去实际操作第It个赌博机所得到的奖赏，将n次操作的差值累加，就是悔值函数的值。

一个高手可以让悔值函数的方差最小

上限置信区间策略（Upper Confidence Bound Strategies，UCB）

UCB可以在探索-利用之间取得平衡，是一种较为成功的策略学习方法

蒙特卡洛树搜索UCT

将UCB应用于游戏树的搜索方法，在2006年提出。

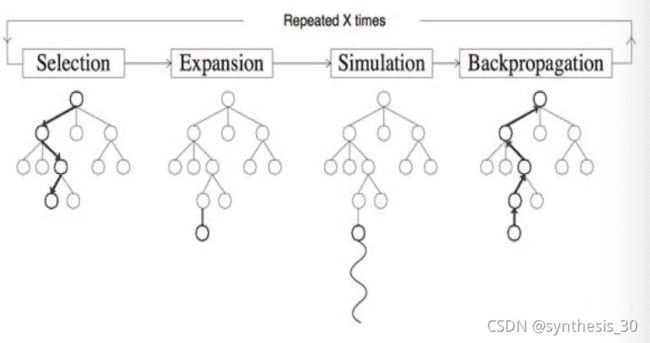
包括4步骤：选择、扩展、模拟、反向传播

 

两种策略学习机制：

搜索树机制：从已有的搜索树中选择或创建一个叶子结点（选择&拓展），搜索树策略需要在利用和探索之间保持平衡

模拟策略：从非叶子结点出发模拟游戏，得到游戏仿真结果 

使用蒙特卡洛树搜索的原因：

MCTS基于采样来得到结果，而非穷尽湿枚举。

例子：围棋