SVM 原理详细推导
SVM 原理详细推导
- 1 硬间隔最大化
-
- 1.1 函数间隔与几何间隔
- 1.2 间隔最大化
- 1.3 凸二次规划问题求解
- 1.4 一个求解例子
- 2 软间隔最大化
- 3 线性不可分问题
- 参考
SVM 是一个分类模型,如果训练数据可以完全用一个超平面分开,则称数据集为完全线性可分的,这时可以采用硬间隔最大化建立带约束问题的最优化,此优化为凸二次规划,凸二次规划问题可以通过拉格朗日对偶性转为拉格朗日函数,转而用SMO算法求解;但现实中大部分数据集不满足完全线性可分,也就是有一些数据会分错,这时可以通过一个松弛变量,让问题同样转为凸二次规划问题;但有许多问题就是线性不可分的,这时就需要将输入向量转为更高维的向量,使得向量在高维空间为线性可分,这就要用到核技巧
1 硬间隔最大化
输入数据 { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . ( x N , y N ) (x_1,y1),(x_2,y_2),...(x_N,y_N) (x1,y1),(x2,y2),...(xN,yN)} 为线性可分数据集(即存在一个超平面将数据集完全分开), 可用一个超平面 w x + b = 0 wx+b=0 wx+b=0(由法向量 w w w 和截距 b b b 确定)将数据集分为两部分,法向量指向的一侧是正类,另一部分是负类
1.1 函数间隔与几何间隔
超平面 w x + b = 0 wx+b=0 wx+b=0 确定之后, ∣ w x i + b ∣ |wx_i+b| ∣wxi+b∣ 值就可以表示 x i x_i xi 点距超平面的远近 (两者相减 ( w x i + b ) − ( w x + b ) = ( w x i + b ) − 0 = w x i + b (wx_i+b)-(wx+b)=(wx_i+b)-0=wx_i+b (wxi+b)−(wx+b)=(wxi+b)−0=wxi+b)。 w x i + b wx_i+b wxi+b 符号与 y i y_i yi 相同( y i y_i yi 取值 +1 或 -1, y∈{1,-1})两者相乘即为绝对距离 ∣ w x i + b ∣ |wx_i+b| ∣wxi+b∣,超平面与点的间隔为函数间隔:

所有点中与超平面最小距离定义为 γ ^ \hatγ γ^:

在函数间隔中,如果同比例改变超平面的法向量 w w w 和截距 b b b ,比如同时乘 2,超平面没变但函数间隔却增大了 2 倍。可以对w 施加约束,使得函数间隔为确定值,这时侯函数间隔成为几何间隔,也即点到平面的距离:
γ i = ( w ∗ x i + b ∣ ∣ w ∣ ∣ ) γ_i= (\frac{w*x_i+b}{||w||}) γi=(∣∣w∣∣w∗xi+b)
∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣为 w w w 的 L 2 L_2 L2 范数,同样 y i y_i yi与距离同符号,距离的绝对值为
γ i = y i ( w ∗ x i + b ∣ ∣ w ∣ ∣ ) γ_i= y_i(\frac{w*x_i+b}{||w||}) γi=yi(∣∣w∣∣w∗xi+b)
几何间隔的最小值为
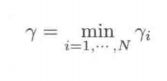
1.2 间隔最大化
实际上几何间隔 γ i γ_i γi 也表示将样本点分开时的确信程度, γ i γ_i γi 值越大,则分开的确信程度也越大,为使得所有点到超平面的几何距离最大化,就需要使得最小的几何间隔 γ γ γ 最大,(注: s.t.表示满足的条件,所有点到平面的距离都应该大于等于最小距离):

函数间隔与几何间隔满足如下关系(带帽的为函数间隔):

最小几何间隔与最小函数间隔关系就为:
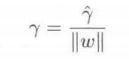
根据以上函数间隔与几何间隔关系,函数

就可以变为:

因为求以上极值的方法,与函数间隔的实际大小没有关系,所以可以假设最小函数距离为 γ ^ = 1 \hatγ=1 γ^=1
另外,求 m a x ( 1 ∣ ∣ w ∣ ∣ ) max (\frac{1}{||w||}) max(∣∣w∣∣1) ,也即是求 m i n ( 1 2 ∣ ∣ w ∣ ∣ 2 ) min(\frac{1}{2}{||w||^2}) min(21∣∣w∣∣2) ,于是优化问题转化为:

这是一个凸二次规划问题
1.3 凸二次规划问题求解
上一小节的原始问题为凸二次规划问题,原始问题需要用到拉格朗日对偶性转为拉格朗日函数,通过求解拉格朗日函数得到原始问题的最优解。同时,转为对偶问题还有其它优点:1、对偶问题更容易求解, 2、引入核函数,将svm 推广到非线性分类问题

首先构建拉格朗日函数,将原始问题转为对偶的极大极小值问题,通过把 α 当作常数,w,b为变量求极小值,随后对包含 α 变量的极小值求极大值:

最后求解 α ∗ α ^* α∗ 需要用到 SMO 算法,求出 α ∗ α ^* α∗ 之后就可以求得 w ∗ w^* w∗ 和 b ∗ b^* b∗, 这时的解一定满足 KKT 条件
观察 KKT 第三个条件
α ∗ ( y i ( w ∗ x i + b ∗ ) − 1 ) = 0 α^*(y_i(w^*x_i+b^*)-1)=0 α∗(yi(w∗xi+b∗)−1)=0
当 ( y i ( w ∗ x i + b ∗ ) − 1 ) > 0 (y_i(w^*x_i+b^*)-1)>0 (yi(w∗xi+b∗)−1)>0 时,必有 α ∗ = 0 α^*=0 α∗=0; ( y i ( w ∗ x i + b ∗ ) − 1 ) = 0 (y_i(w^*x_i+b^*)-1)=0 (yi(w∗xi+b∗)−1)=0 时, α ∗ α^* α∗ 可以不必为 0,
将 w ∗ w* w∗和 b ∗ b* b∗代入 w x + b wx+b wx+b 中, 最后的预测公式就为 f ( x ) = s i g n ( ∑ 1 N α ∗ y i ( x ⋅ x i ) + b ∗ ) f(x) = sign(\sum _{1}^{N}α ^*y_i(x\cdot x_i)+b^*) f(x)=sign(∑1Nα∗yi(x⋅xi)+b∗) 。预测公式中除了满足 y i ( w ∗ x i + b ∗ ) − 1 = 0 y_i(w^*x_i+b^*)-1=0 yi(w∗xi+b∗)−1=0 的 α ∗ α^* α∗ 不为 0 之外,其它的 α ∗ α^* α∗ 均为 0,也即预测结果仅由满足 ( y i ( w ∗ x i + b ∗ ) − 1 ) = 0 (y_i(w^*x_i+b^*)-1)=0 (yi(w∗xi+b∗)−1)=0 的点决定,满足此公式的点也即为支持向量
1.4 一个求解例子
待补充
2 软间隔最大化
在实际情况中,并不是所有点都能正确地分为正类或负类,也即不满足函数间隔大于等于 1 的约束条件,为了解决这个问题,可以为每个样本的函数间隔加一个松弛变量 ξ i ≥ 0 ξ_i≥0 ξi≥0 ,使得函数间隔加上松弛变量大于等于 1,约束条件变为:
y i ( w ∗ x i + b ) + ξ i ≥ 1 y_i(w*x_i+b)+ξ_i≥1 yi(w∗xi+b)+ξi≥1
同时对于每一个松弛变量都需要付出一个代价 ξ i ξ_i ξi,目标函数变为

C>0 称为惩罚函数,C 减小时,对误分类的惩罚减小,当模型过拟合时,我们可以减小 C 值
3 线性不可分问题
训练好的模型预测公式为
f ( x ) = s i g n ( ∑ 1 N α ∗ y i ( x ⋅ x i ) + b ∗ ) f(x) = sign(\sum _{1}^{N}α ^*y_i(x\cdot x_i)+b^*) f(x)=sign(1∑Nα∗yi(x⋅xi)+b∗)
实际中数据不一定线性可分,所以需要将输入向量 x 映射到高维空间中,使得数据在高维空间中线性可分,映射函数为 φ ( x ) φ(x) φ(x),映射后两个向量的点积称为核函数
K ( x , y ) = φ ( x ) ⋅ φ ( y ) K(x,y)=φ(x)\cdotφ(y) K(x,y)=φ(x)⋅φ(y)
将核函数引入我们的预测函数中,由此函数变为
f ( x ) = s i g n ( ∑ 1 N α ∗ y i ( K ( x , x i ) + b ∗ ) f(x) = sign(\sum _{1}^{N}α ^*y_i(K(x,x_i)+b^*) f(x)=sign(1∑Nα∗yi(K(x,xi)+b∗)
从此函数可以看出其实我们并不正真需要计算x的实际映射结果 φ ( x ) φ(x) φ(x),只要知道两个向量映射后的点积即可,也即直接计算 K ( x , y ) K(x,y) K(x,y)。可以形象化的理解为向量 x 和 y都映射到高维空间后两者的点积即为核函数结果,我们不关于它们映射到了什么样的空间,只关注最后的结果
关于 SVM 的使用可以参考 scikit-learn 中 SVM 的使用
参考
1 《统计学习方法》 李航
2 SVM-支持向量机原理详解与实践

