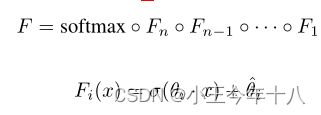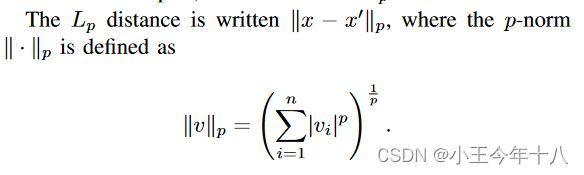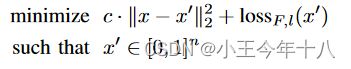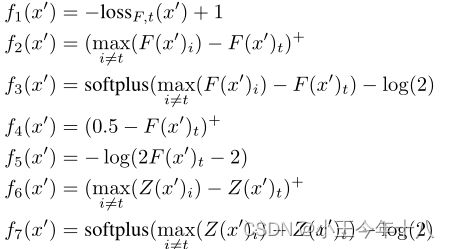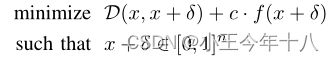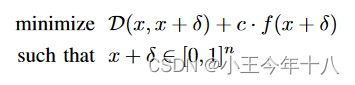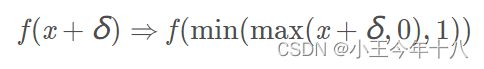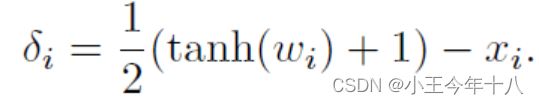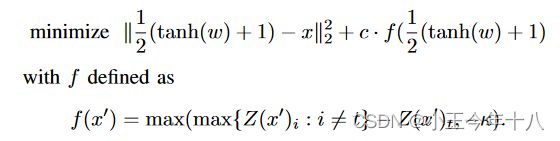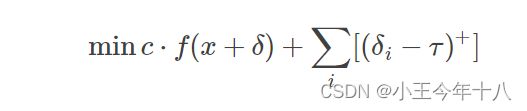C&W攻击算法
C&W是一种基于优化的攻击方式，它同时兼顾高攻击准确率和低对抗扰动的两个方面。首先对抗样本需要用优化的参数来表示，其次在优化的过程中，需要达到两个目标，目标一是对抗样本和对应的干净样本应该差距越小越好；目标二是对抗样本应该使得模型分类错，且错的那一类的概率越高越好。
目录
主要贡献
神经网络
对抗样本
距离度量
攻击算法
L-BFGS
Fast Gradient Sign
JSMA
Deep fool
C&W攻击算法
常数c的选择
盒约束问题
攻击
L2攻击
L0攻击
L∞攻击
主要贡献
本文作者还将L0，L2，L∞这三种距离度量引入到了C&W攻击中，这三种攻击的加入使得在较小的扰动下，就能有较高的攻击准确率。
模型蒸馏是对抗样本的有效的防御手段，CW攻击可以攻破防御性蒸馏中模型，高置信度的使模型出现误分类。
在定义攻击中，作者提出了七个优化目标，并系统地评估了目标函数的选择，目标函数的选择可以显著地影响攻击的效果，实验显示论文中的优化目标函数 f(6) 是所有优化目标中效果最好的。
神经网络
文章重点研究了神经网络作为m-class分类器的应用。用softmax函数计算网络的输出。
可以表示为：
其中F为包含softmax函数的完整神经网络，Z(x)=Z为除了softmax之外的所有层的输出。softmax函数的输入称为logits。
神经网络通常由层组成。
本文主要使用了ReLU激活函数，
对抗样本
文章考虑三种不同的方法来选择目标类，在有针对性的攻击中:
- 平均情况：随机选择不正确的标签
- 最好情况：选择攻击难度最小的标签
- 最坏情况：选择攻击难度最难的标签
距离度量
本文中所用到的距离度量的方式属于Lp规范
攻击算法
L-BFGS
Szegedy提出了盒约束的对抗样本生成的方法
考虑求解的问题，将其转换成为了
是将一个图像映射到正实数的函数，常用交叉熵损失函数。c是一个常数，使用二分搜索或者其他一维优化方法自适地更新c。
Fast Gradient Sign
该方法与L- bfgs方法有两个关键区别:首先，它针对L∞距离度量进行了优化，其次，它主要设计为快速，而不是产生非常接近的对抗示例。
JSMA
Papernot等人引入了一种在L0距离下优化的攻击，称为基于雅可比矩阵的显著映射攻击(JSMA)。 这是一种贪婪算法，每次选择一个像素修改，每次迭代增加分类目标。使用梯度计算显著性图，在显著图的位置上修改像素，能对模型分类错误产生巨大影响。
Deep fool
Deepfool是一种基于超平面分类的攻击算法。这是我之前的阅读笔记。
C&W攻击算法
D代表二者之间的距离，可以是各种范数。
C：分类器 t代表想要的target label
![x+\delta \in [0,1]^{n}](http://img.e-com-net.com/image/info8/cd1202ae08184fbfa169118b9f9c2f78.gif){kind=small}
限制增加扰动后值的范围
约束C(x+δ)=t是高度非线性的，现有算法难以解决，定义一个目标函数f，当且仅当 f(x+δ)≤0时， C(x+δ)=t。f有许多可能的选择
其中s是正确的分类
是max(e,0)的缩写 。softplus(x)=log(1+exp(x)),
是对于x的交叉熵损失。此时，函数可以写成：
其中c>0是一个适当选择的常数在c>0时上面二者是等价的，再用Lp范数实例化距离度量D之后，整个问题就变成了在给定x之后，找一个δ，其中δ：
上述提到七种目标函数中，f2，f3,f4效果欠佳，f6在这七种策略中表现最好：需要的扰动一般是最小，且成功率高
常数c的选择
我们发现选择c的最佳方法通常是使用c的最小值，实验中，选择二分查找来确定c
盒约束问题
为了解决0≤xi+δ≤1,本文采用了三种方法来解决。
Projected gradient descent：每实施一步梯度下降，就把计算的结果限制在box内，该方法的缺点就是每次传入下一步的结果都不是真实值。对于使用复制更新其的梯度下降不适用。
Clipped gradient descent：并没有真正地裁减x而是直接把约束加入到目标函数中，即
这种方法，只是对目标函数进行了约束，可能会存在xi+δ超过最大值的情况，这样就会出现梯度为0的结果，以至于x i即使减少，从梯度角度也无法检测到。
Change of variables：通过引入变量 使得xi+δ 满足box约束，其方法为
实验结果表明，Projected gradient descent在处理盒约束是优于另外两种的，但是Change of variables寻求的扰动一般都是比较小的。
攻击
L2攻击
这个f其实就是之前测试中的f6，是最佳目标函数。只是对k解除了必须为0的约束。
这个公式的优点是他允许人们控制期望的置信度。
参数κ的目的是控制对抗样本的强度：κ越大，对抗样本的分类越强。这使我们可以通过增加κ来生成高可信度的对抗样本
由于梯度下降的贪婪搜索不能保证找到最优解，并且可能陷入局部极小值。采用多起点梯度下降：选择多个接近原始图像的随机起点，对这些点进行梯度下降，进行固定次数的迭代。
L0攻击
因为L0距离是无法微分的，所以作者采用迭代的方法，使用L2 Attack来确定哪些像素不重要，对不重要的像素点就固定着。
L∞攻击
该攻击方法不是完全可微的。
在每次迭代之后，如果对所有的i都有
,将
减少0.9倍并重复;否则，终止搜索。
再次，我们必须选择一个好的常数 c用于
攻击。采用与 L0攻击相同的方法:首先将c设置为非常低的值，然后以此c值运行攻击。如果失败， 加倍c并重试，直到成功。如果c超过固定阈值，中止搜索。
在每次迭代中使用热启动进行梯度下降，作者指出该算法的速度与之前的L2算法(使用单个起点)一样快。