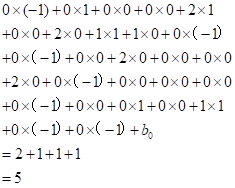【深度学习】卷积神经网络CNN入门介绍
一、卷积神经网络的引入
1.1 卷积神经网络的结构
如下所示,
其中第一层为卷积层,第二层为池化层,又称为降采样层或者下采样层,第三层为卷积层,第四层为池化层,最后把池化的结果拉平成一条长向量,传入到底层全连接层中,最后输出结果。
所有的用于图像分类的卷积神经网络,结构都是大同小异的。
基本结构都是如下所示,
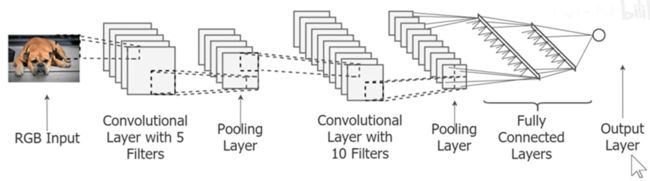
卷积 → \rightarrow →池化 → \rightarrow →卷积 → \rightarrow →池化 → \rightarrow →全连接 → \rightarrow →全连接 → \rightarrow →输出
卷积方式可以多种,信息传递的流或者路径也可以不同,但基本结构都是一样。
1.2 卷积神经网络各层的作用
卷积层:用于提取图像的底层特征;
池化层:用于防止过拟合的产生,并减少数据维度;
全连接层:用于汇总之前的卷积层和池化层得到的图像的底层的特征和信息。
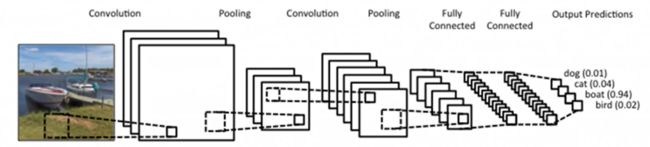
输出可以是softmax输出,比如多种输出,如猫,狗和鸟的分类输出,也可以是sigmoid二分类输出,比如输出是不是狗。
如果我们用softmax分类的话,相当于是一个归一化,输出的是每一个种类对应原图中的概率,概率最大的就是所属的类。
1.3 卷积核
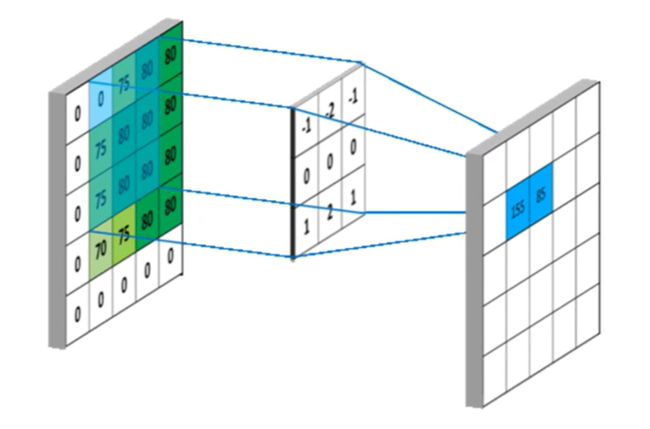
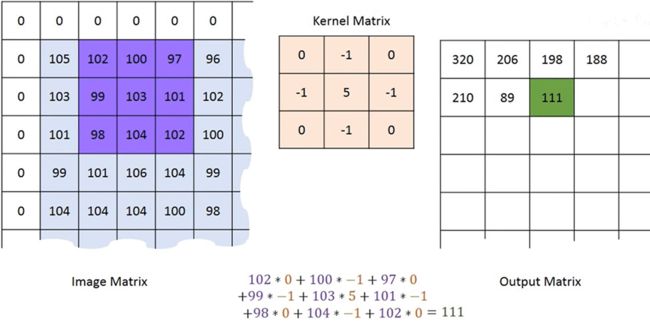
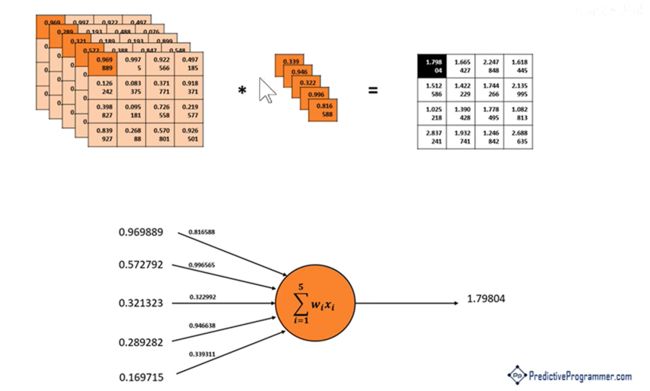
中间那层随着浮动位置变化并不会改变,称为卷积核,卷积核在原图上进行滑动,与对应元素的进行相乘,最后把乘积的和求出来。
卷积核光顾到的地方叫做感受野,就好比我们人眼看东西,目光注视到了那一块,我们就感受到了那一块。
我们定格一个瞬间:
下图演示了卷积运算的操作。与原图相比,这个外面补了一圈0,这个叫做padding。
前面可以发现,输入图像与卷积核进行卷积后的结果中损失了部分值,输入图像的边缘被“修剪”掉了(边缘处只检测了部分像素点,丢失了图片边界处的众多信息)。这是因为边缘上的像素永远不会位于卷积核中心,而卷积核也没法扩展到边缘区域以外。
这个结果我们是不能接受的,有时我们还希望输入和输出的大小应该保持一致。为解决这个问题,可以在进行卷积操作前,对原矩阵进行边界填充(Padding),也就是在矩阵的边界上填充一些值,以增加矩阵的大小,通常都用“0”来进行填充的。
通过填充的方法,当卷积核扫描输入数据时,它能延伸到边缘以外的伪像素,从而使输出和输入size相同。
我们来看一次2*2的卷积核,输出叫做feature map。
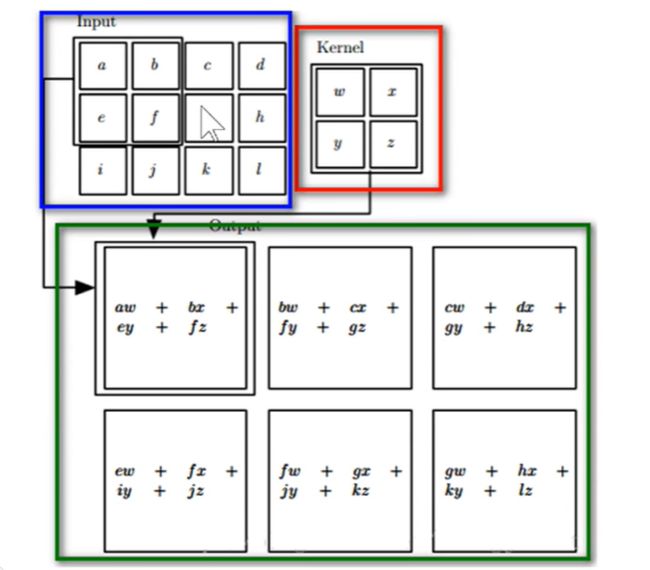

也就是说,卷积这个操作,把大的原始图像转换为小的输出。有多少个卷积核就有多少个feature map。
我们用很多个卷积核生成很多个feature map,小feature map来表示对原始的图像进行压缩和特征提取,这就是卷积做的工作。
二、卷积中各种参数的交互式演示
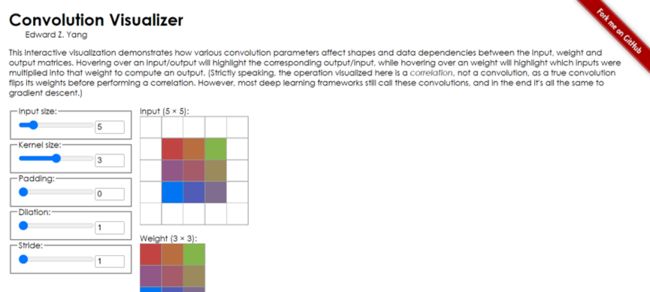
推荐一个在线网页,演示了卷积神经网络各种参数的交互式演示。
https://ezyang.github.io/convolution-visualizer/index.html
白色表示输入的图片,比如input size=5,那么白色的输入区域就是5*5。
卷积核为3,就是图中3*3的彩色图片。
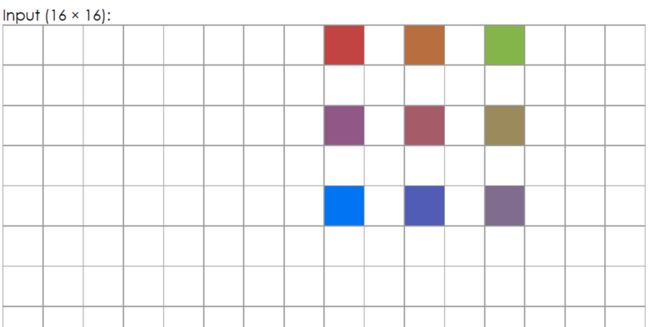
我们增加一层padding:

Dilation表示棋盘,表示我们的卷积核不再是连续的一片,而是跨像素的感受野。它可以捕捉图像中更有效的信息。
Stride表示步长,表示每步按多少的步长进行滑动。
这个网页只是展示了一个通道的图像,以及一个卷积核。
三、多通道图像的卷积
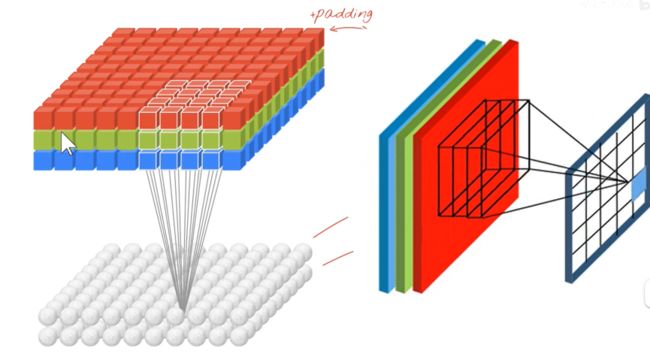
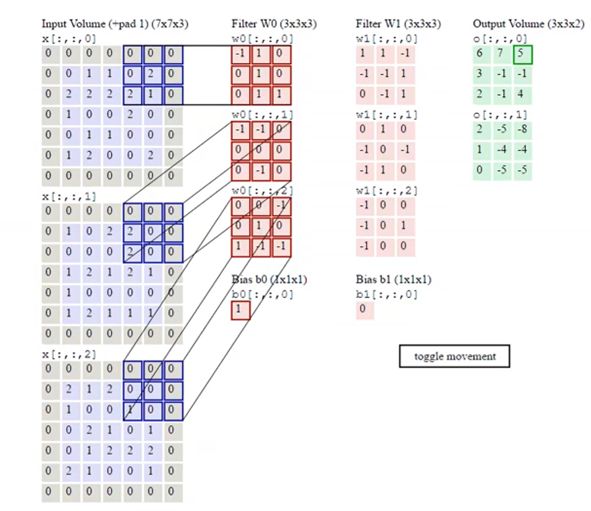
刚刚我们讲解的是二维卷积核在二维图像上的卷积的结果。我们平常见到的大部分彩色图片都是R、G、B三个通道的,在这种情况下,我们的卷积核也要变为R、G、B三个通道的。
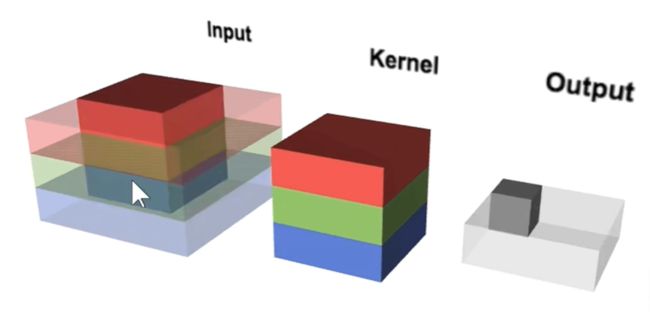
上图中,卷积核中的红色的权重与原图中红色通道的像素进行卷积,绿色的权重与原图中蓝色通道的像素进行卷积,蓝色的权重与原图中蓝色通道的像素进行卷积。
现在是第二个卷积核对图像进行卷积。
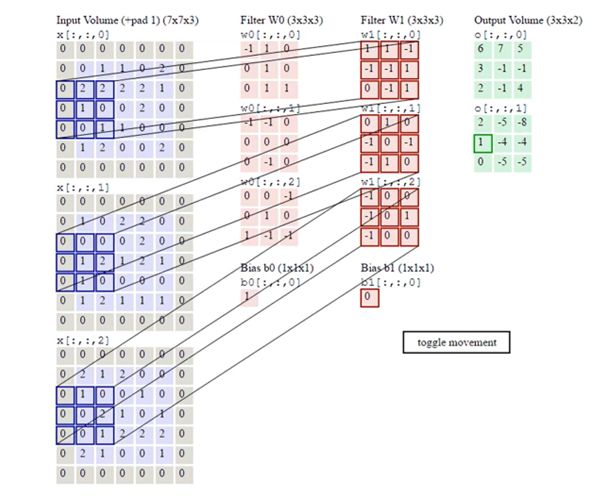
下面的 b 0 b_0 b0和 b 1 b_1 b1为偏置项,需要加上。
卷积是在在提取原图像上的底层特征,有两种情况:
在真实的卷积神经网络里,卷积核不需要我们自己去设置,而是通过机器学习的方法自己找到的。
四、池化层与全连接层
我们已经知道了卷积是怎么回事,每一个卷积核都会生成一个feature map。在真实的卷积神经网络里,卷积核的个数个数是非常多的,每一层都有32、64或256个卷积核。拿上图来说,如果我们有256个卷积核,那么最后就会生成44256个特征图,这样的参数的个数就远远超过了原图的个数。
所以我们需要想办法把生成的feature map的维度降下来,尽量进行数据压缩。这样也可以有效的防止过拟合,这样就有了池化的概念。
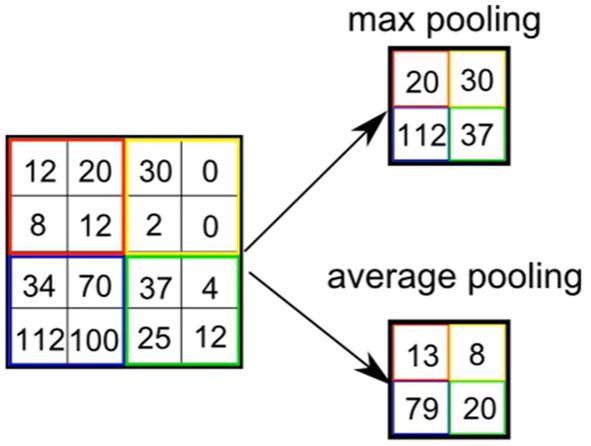
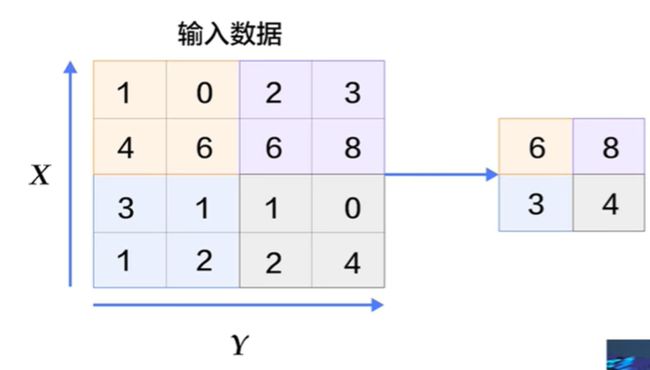
左边是特征图,用一个大框框起来,然后我们选择在里面选择一个值来代表。
下面是一个池化的案例:
用的最多的是最大池化。
五、池化的作用
- 减少参数量
- 防止过拟合
- 可以为卷积神经网络带来平移不变性
如下面的是卷积后的4,上面的小一点的是池化后的4。
有了池化层,把池化层拉平成一个长向量,然后喂给全连接神经网络。
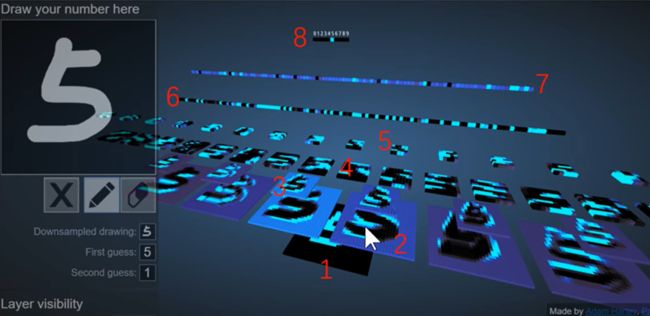
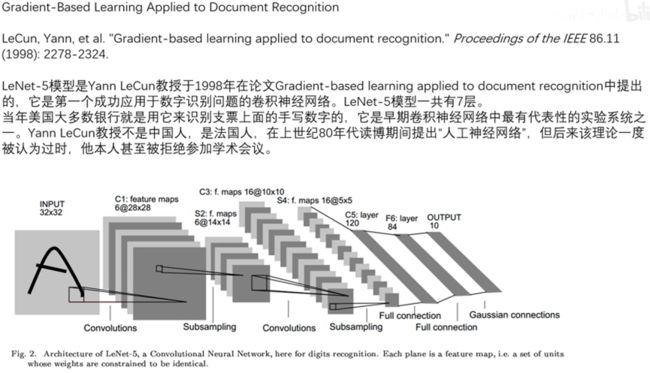
第一层为输入,第二次为卷积层,第三层为池化层,第四层为卷积层,第五层为池化层,第六层为全连接层,第七层全连接,第八层为输出。
步骤如下总结:
1) 把手写字体图片转换成像素矩阵;
2) 对像素矩阵进行第一层卷积运算,生成六个feature map;
3) 对每个feature map进行下采样(也叫做池化),在保留feature map特征的同时缩小数据量。生成六个小图,这六个小图和上一层各自的feature map长的很像,但是尺寸缩小了。
4) 对六个小图进行第二层卷积运算,生成更多的feature map;
5) 对第二次卷积生成的feature map进行下采样;
6) 第一层全连接层;
7) 第二层全连接层;
8) 高斯连接层,输出分类结果。
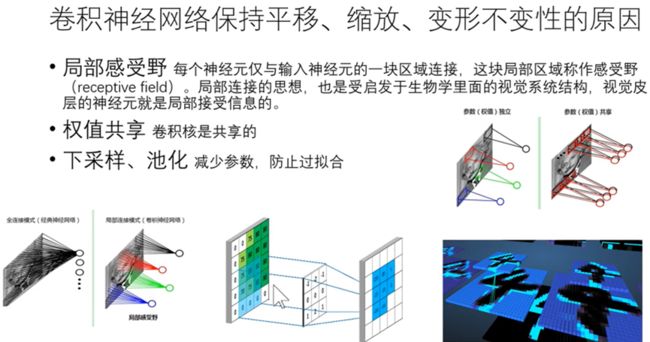
六、卷积神经网络各层的作用
解释了为什么具有平移不变性。
七、卷积神经网络的鼻祖
高斯连接层现在不怎么使用了,现在大家一般都使用softmax层。