基于kd树的KNN算法原理以及python实现
k k k近邻算法
算法描述
目标
k k k近邻算法也是一个分类算法,其最终的目的是预测输入的点所属的类别
思想
k k k近邻算法的思想就是将输入的点的类别预测为其周围大多数点的类别,物以类聚
策略
我们在二维的空间下分析策略
如图,有多个实例(点),每个点属于一种类别
这时我们输入一个需要预测的点,则根据其附近类别最多的点决定将其分为紫色
算法
根据以上策略,我们不难得出k近邻算法
-
输入
训练数据集 T = ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) T={(x_1,y_1),(x_2,y_2),...,(x_N,y_N)} T=(x1,y1),(x2,y2),...,(xN,yN)。其中 x i x_i xi是特征向量, y i y_i yi是实例对应的类别。 y i ∈ Y = { c 1 , c 2 , . . . , c k } y_i\in{Y}=\{c_1,c_2,...,c_k\} yi∈Y={c1,c2,...,ck};
需要预测的实例特征向量 x x x
-
输出
实例 x x x所属的类 y y y
-
过程
- 根据给定的距离度量找到训练集 T T T中与 x x x最临近的 k k k个点,涵盖这 k k k个点的 x x x的邻域记作 N k ( x ) N_k(x) Nk(x)
- 在 N k ( x ) N_k(x) Nk(x)中找到个数最多的类别 y y y作为 x x x的类别预测,决策规则如下
y = a r g m a x c j ∑ x i ∈ N k ( x ) I ( y i = c j ) , i = 1 , 2 , . . . , N ; j = 1 , 2 , . . . , k (1) y=\underset{c_j}{argmax}\sum_{x_i\in{N_k(x)}}I(y_i=c_j),i=1,2,...,N;j=1,2,...,k\tag{1} y=cjargmaxxi∈Nk(x)∑I(yi=cj),i=1,2,...,N;j=1,2,...,k(1)
这个算法过程中有两个问题
- 距离度量是什么
- k k k选取几个
距离度量
算法中要找到最邻近的 k k k个点,那么就要有一个距离的度量方法
度量方法有很多种,欧式距离,曼哈顿距离等,这些距离都有一个通式
L p ( x i , x j ) = ( ∑ l = 1 n ∣ x i l − x j l ∣ p ) 1 p (2) L_p(x_i,x_j)=(\sum_{l=1}^n|x_i^{l}-x_j^{l}|^p)^{\frac{1}{p}}\tag{2} Lp(xi,xj)=(l=1∑n∣xil−xjl∣p)p1(2)
其中 x i x_i xi和 x j x_j xj均为特征向量。 x i = ( x i ( 1 ) , x i ( 2 ) , . . . , x i ( n ) ) T x_i=(x_i^{(1)},x_i^{(2)},...,x_i^{(n)})^T xi=(xi(1),xi(2),...,xi(n))T
当p=1时,就是曼哈顿距离
当p=2时,就是欧氏距离,也就是我们熟知的直线距离
一般我们选择欧式距离当作度量单位,也就是所谓的直线距离
k的选择
k的选取很重要,不能过大也不能过小
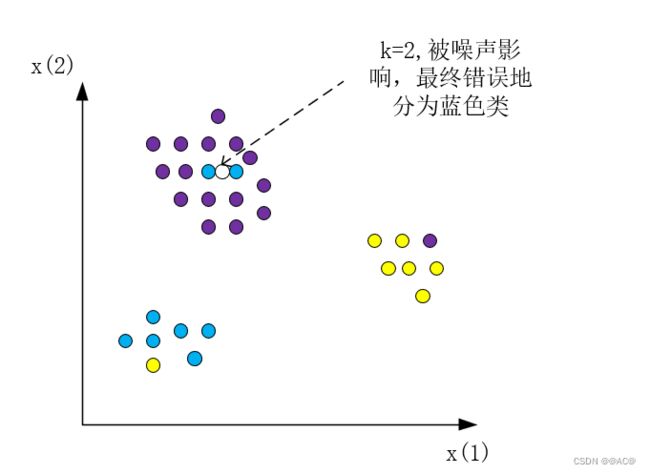
如果k选取过小,则容易被噪声影响。如下,只有与输入实例较近的训练实例会对预测产生影响,如果较劲的实例是噪音,就有可能误分类
如果k选取过大,这时离输入实例较远的点也对实例产生了影响,有可能产生误差
一般都先取一个比较小的k值,然后使用交叉验证法选取最优的k值
k d kd kd树优化
引言
由算法描述我们可以知道,实现 k k k近邻算法,我们需要针对训练数据进行快速 k k k近邻搜索,也就是找到离输入点最近的 k k k个点
k k k近邻算法最简单的是线性扫描,计算输入点到每个训练实例的距离,然后比较,但这样训练集大的时候会非常耗时
为了提高这个搜索效率,减少计算距离次数,有很多方法, k d kd kd树就是其中一个
k d kd kd树定义
k d kd kd树是一种对空间中的实例点进行存储以便对其进行快速检索的树形数据结构,是二叉树,表示对 k k k维空间进行划分
这个 k k k不是 k k k临近那个 k k k,而是表示空间的维度
构造 k d kd kd树
根据 k d kd kd树的定义,我们很容易得到构造 k d kd kd树的方法
我们一个实例,即特征向量有多个特征,每个特征代表空间的一个维度,一个坐标轴
x = ( x ( 1 ) , x ( 2 ) , . . . , x ( k ) ) T x=(x^{(1)},x^{(2)},...,x^{(k)})^T x=(x(1),x(2),...,x(k))T
构造 k d kd kd树就是不断用垂直于坐标轴的超平面将 k k k维空间进行切分,构成一系列 k k k维超矩形区域, k d kd kd树每个节点对应一个 k k k维度的超矩形区域
算法描述
-
输入: k k k维空间数据集 T = { x 1 , x 2 , . . . , x N } T=\{x_1,x_2,...,x_N\} T={x1,x2,...,xN}
其中 x i = ( x i ( 1 ) , x i ( 2 ) , . . . x i ( k ) ) T , i = 1 , 2 , . . . N x_i=(x_i^{(1)},x_i^{(2)},...x_i^{(k)})^T,\ \ i=1,2,...N xi=(xi(1),xi(2),...xi(k))T, i=1,2,...N
-
输出: k d kd kd树
-
过程
-
开始: 构造根节点,
根结点对应包含T(所有实例)的K维空间的超矩形区域选择 x ( 1 ) x^{(1)} x(1)为坐标轴, T T T中所有实例的 x ( 1 ) x^{(1)} x(1)坐标的中位数作为切分点,用切分点与坐标轴 x ( 1 ) x^{(1)} x(1)垂直的超平面将根节点对应的超矩形区域分成两个区域
x ( 1 ) x^{(1)} x(1)比切分点的 x ( 1 ) x^{(1)} x(1)小的切到左边,大的切到右边
落在切分超平面上的点就是根节点
如果有多余的切分点,那么这里切分点只留一个其他的分到左边或者右边
-
重复: 对生成的子节点重复上面的切分步骤,直到划分的两个子区域没有实例
对深度为 j j j的节点,选 x l x^l xl为切分坐标轴, l = j ( m o d k ) + 1 l=j(modk)+1 l=j(modk)+1
落在超平面上的节点保存在该节点
-
构造例子
给定一个二位空间数据集如下,构造一个 k d kd kd树
T = { ( 2 , 3 ) T , ( 5 , 4 ) T , ( 9 , 6 ) T , ( 4 , 7 ) T , ( 8 , 1 ) T , ( 7 , 2 ) T } T=\{(2,3)^T,(5,4)^T,(9,6)^T,(4,7)^T,(8,1)^T,(7,2)^T\} T={(2,3)T,(5,4)T,(9,6)T,(4,7)T,(8,1)T,(7,2)T}
解
-
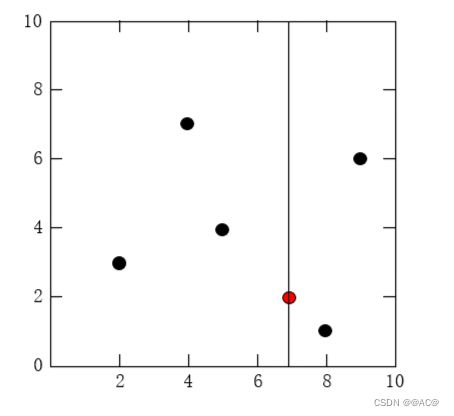
首先我们选择 x ( 1 ) x^{(1)} x(1)轴对T进行划分,中位数是7,以点 ( 7 , 2 ) T (7,2)^T (7,2)T作为切分点,沿着垂直于 x ( 1 ) x^{(1)} x(1)轴的超平面将矩形区域分为两个超矩形区域。
-
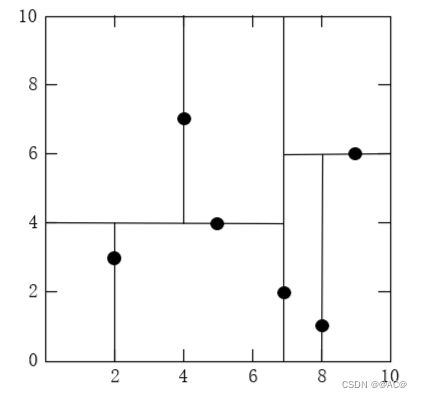
对于左边部分,其深度为1,选择 x ( 2 ) x^{(2)} x(2)轴进行划分,中位数是4,点 ( 5 , 4 ) T (5,4)^T (5,4)T作为切分点,此时 ( 5 , 4 ) T (5,4)^T (5,4)T对应了左边整个超矩形
对应的概念在后面很重要
- 一直划分下去,最后构造的 k d kd kd树结果如下
用树的形式表示如下
搜索 k d kd kd树
目的
搜索 k d kd kd树,最终目的是为了帮助我们找到 k k k个与输入点邻近的点,但是为了方便理解,这里先讲解一下如何搜索最邻近的点
算法描述-最邻近点
-
输入:已构造的 k d kd kd树;目标点 x x x
-
输出: x x x的最邻近点
-
过程
-
在 k d kd kd中找出其对应超矩形区域包含目标点 x x x的叶结点
从根结点开始,递归向下访问
与 k d kd kd树构造时类似,如果目标点当前维度小于切分点的坐标,则移动到左结点,大于则移动到右结点,直到找到叶结点
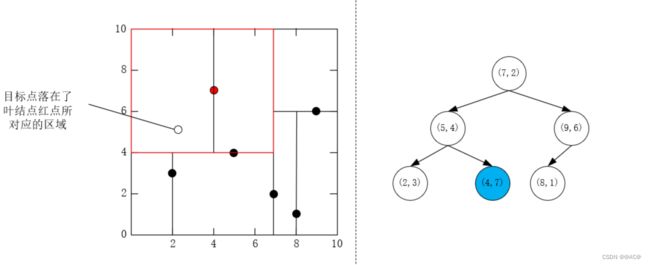
-
将找到的叶结点标记为"当前最近点"
在这片区域内,这个叶结点是与目标节点最近的(叶结点所对应的区域只有一个点,就是他自己)
但是可能这个区域旁边的区域的结点会比这个结点离目标节点更近,所以该结点是"当前最近点",而不是最近点
-
递归向上回退,对于回退到的每个结点
-
如果该结点保存的实例比"当前最近点"距离目标点更近,则以该点做为"当前最近点"
-
且由于我们是从一个区域回退到该点,所以还应检查该点另一个子结点对应的区域(如果有的话):
只需检查另一个子结点对应的区域是否与
以目标点为球心、以目标点与"当前最近点"间的距离为半径的超球体相交"相交直接用距离比较就行
如果相交,则有可能在另一个子结点对应的区域内存在距目标点更近的点,需要移动到另一个子结点进行近邻搜索
如果不相交,则继续向上回退
因为不相交时,那片区域一定不会有比"当前最近点"更近的点了
-
- 回退到根结点时搜索结束,最后的"当前最近点"为 x x x的最近邻点
-
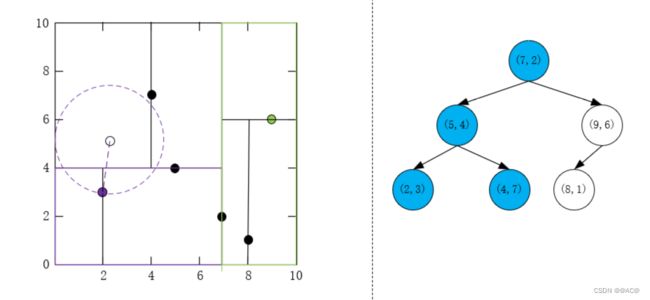
过一遍例子
上面的算法过程中的图是辅助理解,下面来过一遍例子,训练实例如下,输入是 ( 2.2 , 4 , 5 ) T (2.2,4,5)^T (2.2,4,5)T
T = { ( 2 , 3 ) T , ( 5 , 4 ) T , ( 9 , 6 ) T , ( 4 , 7 ) T , ( 8 , 1 ) T , ( 7 , 2 ) T } T=\{(2,3)^T,(5,4)^T,(9,6)^T,(4,7)^T,(8,1)^T,(7,2)^T\} T={(2,3)T,(5,4)T,(9,6)T,(4,7)T,(8,1)T,(7,2)T}
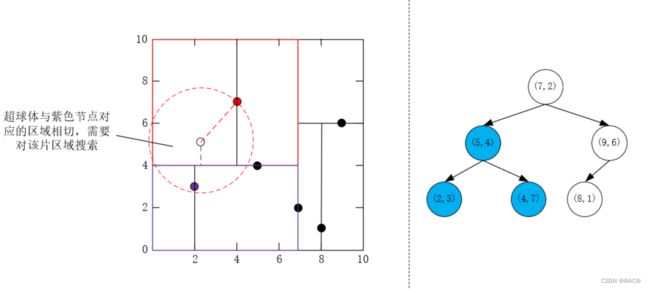
- 首先根据划分搜索到第一个结点为 ( 4 , 7 ) T (4,7)^T (4,7)T,将其当作"当前最近点"
- 回退到其父节点 ( 5 , 4 ) T (5,4)^T (5,4)T,其与目标点的距离比"当前最近点"到目标点的距离大,不操作
- 考虑 ( 5 , 4 ) T (5,4)^T (5,4)T的另一个子节点 ( 2 , 3 ) T (2,3)^T (2,3)T,其对应区域与超球体相交,该区域有可能有更近的点,对其进行近邻搜索
找到比"当前最近点"距离目标点更近的点,更新"当前最近点"
-
回退到点 ( 7 , 2 ) T (7,2)^T (7,2)T,其与目标点的距离比"当前最近点"到目标点的距离大,不操作
-
检查点 ( 9 , 6 ) T (9,6)^T (9,6)T对应的区域,与超球体不相交,里面不可能有比"当前最近点"更近的点,不搜索
- 回退到根节点,最终得到最近点 ( 2 , 3 ) T (2,3)^T (2,3)T
时间复杂度
由上述算法我们可以发现,若一个节点另一个子区域与超球体不相交,则可以直接省掉一刻子树,大大缩短了搜搜时间
如果实例点随机分布, k d kd kd树的平均搜索复杂度是 O ( l o g N ) O(logN) O(logN)
k d kd kd 树更适用于训练实例数远大于空间维数时的近邻搜索,当空间维数接近训练实例数时,它的效率会迅速几乎接近线性扫描
算法描述- k k k近邻点
思想
在了解了如何寻找最近邻点之后,下面来看看怎么找 k k k个近邻点
一种简单的方法是直接进行k次最邻近搜索,下面看看另一种方法怎么做
其基本思想是,维护一个数组,存放与目标点最相邻的k个点
每次回退到一个结点时:
- 如果数组没满,那么直接将结点放入数组
- 如果数组满了,那么用
数组中距离目标点最远的结点的到目标点的距离与当前结点到目标点的距离比较判断是否用当前结点更新数组 - 如果数组没满,直接进入该结点的另一个子节点的区域
- 如果数组满了,则用
数组中距离目标点最远的结点的与目标点形成超球体和该节点另一个子节点的区域比较是否相交,相交则进入另一篇区域相交说明数组中至少有一个点会被另一片区域中的点替代
最后剩下的数组里的 k k k个点就是答案
算法
-
输入:已构造的 k d kd kd树;目标点 x x x
-
输出: x x x的 k k k个邻近点
-
过程
-
在 k d kd kd中找出其对应超矩形区域包含目标点 x x x的叶结点
-
维护一个大小为 k k k的大顶堆,将找到的叶结点插入到堆中
堆的目的是降低时间复杂度
-
递归向上回退,对于回退到的每个结点
-
检查堆是否已满
如果此时堆没满,将该结点插入堆中,更新堆;
如果堆满了,若
该结点到目标点的距离比堆顶的点到目标点的距离小,将堆顶从堆中删除,将该结点插入到堆中,更新堆 -
检查该点另一个子节点对应的区域
- 如果堆没满,直接移动到另一个子结点进行近邻搜索
- 如果堆满了,只需检查另一个子结点对应的区域是否与``以目标点为球心、以目标点与堆顶点间的距离为半径的超球体相交"`
- 如果相交,需要移动到另一个子结点进行近邻搜索
- 如果不相交,则继续向上回退
-
-
最后得到的堆就是 k k k个近邻的点
-
例子
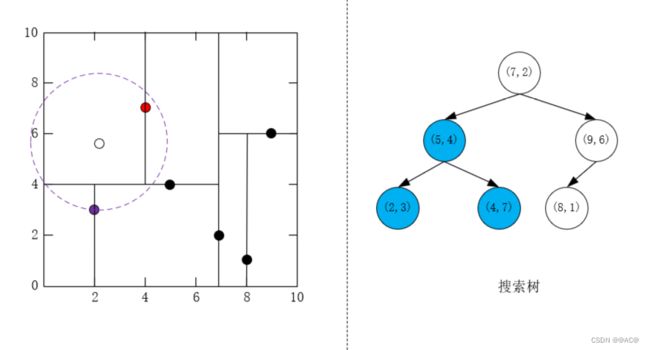
训练数据集如下, k k k为2,输入点为 ( 2.1 , 4.7 ) T (2.1,4.7)^T (2.1,4.7)T
T = { ( 2 , 3 ) T , ( 5 , 4 ) T , ( 9 , 6 ) T , ( 4 , 7 ) T , ( 8 , 1 ) T , ( 7 , 2 ) T } T=\{(2,3)^T,(5,4)^T,(9,6)^T,(4,7)^T,(8,1)^T,(7,2)^T\} T={(2,3)T,(5,4)T,(9,6)T,(4,7)T,(8,1)T,(7,2)T}
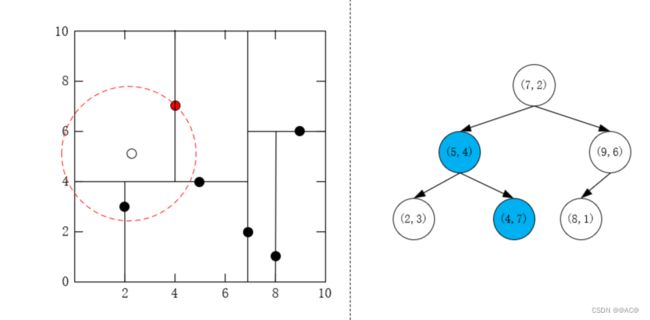
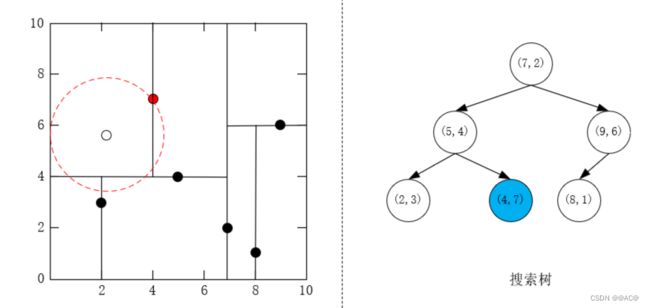
- 一开始搜索到 ( 4 , 7 ) T (4,7)^T (4,7)T,堆大小为1,入堆(堆就不画了)
- 回退到其父节点,堆大小为1,未满, ( 5 , 4 ) T (5,4)^T (5,4)T入堆,并更新堆,此时最大距离点改变
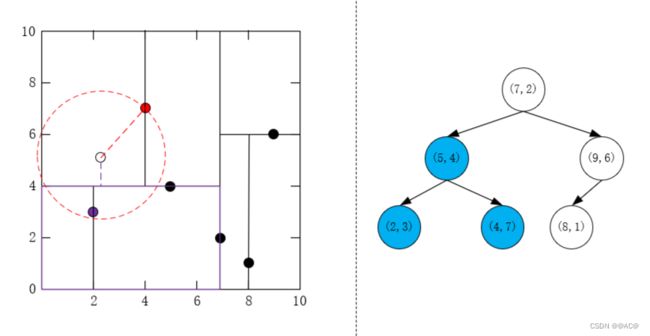
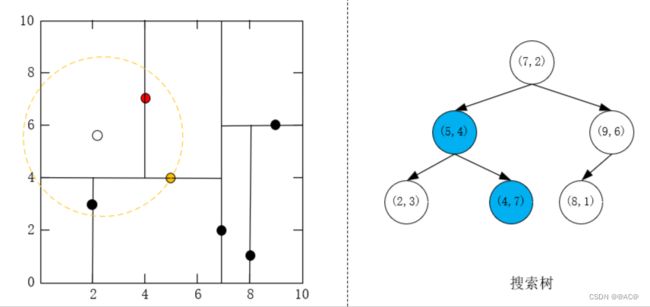
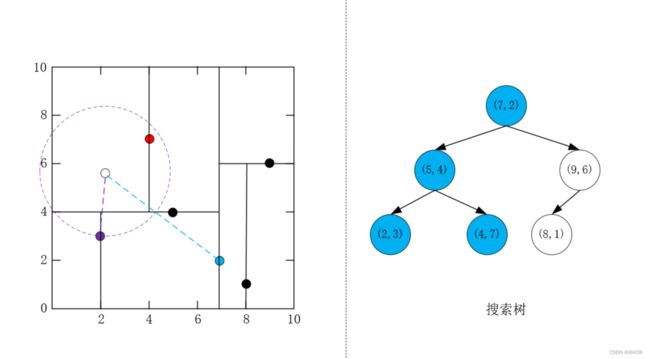
- 由于堆已满且超球体与 ( 5 , 4 ) T (5,4)^T (5,4)T的另一个子节点对应区域相交,则到另一个子节点对应的区域搜索;
发现 ( 2 , 3 ) T (2,3)^T (2,3)T比 ( 5 , 4 ) T (5,4)^T (5,4)T距离目标点近,更新堆
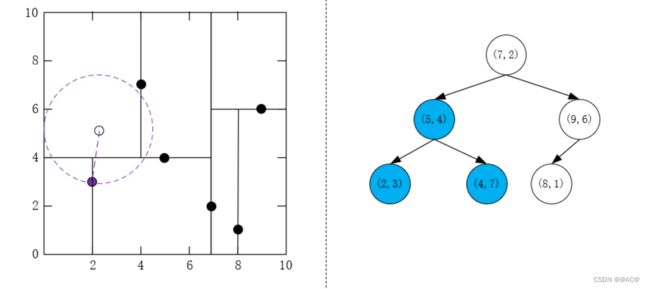
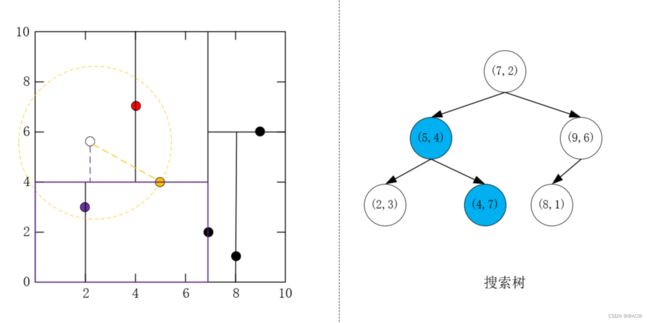
- 回退到 ( 7 , 2 ) T (7,2)^T (7,2)T,由于堆已满,且 ( 7 , 2 ) T (7,2)^T (7,2)T到目标点的距离大于堆顶到目标点的距离,不操作
-
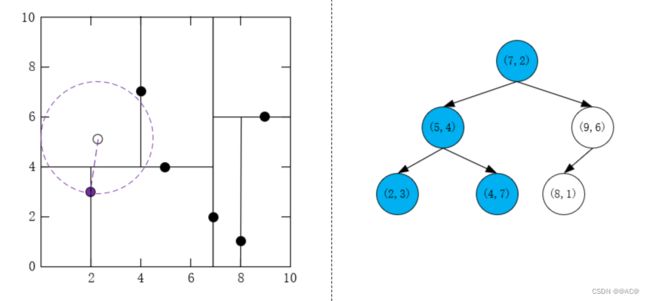
检查 ( 9 , 6 ) T (9,6)^T (9,6)T对应的区域,由于堆已满且该区域与超球体不相交,不移动到 ( 9 , 6 ) T (9,6)^T (9,6)T区域搜索

-
至此搜索结束,搜索到的最终结点是 ( 5 , 4 ) T , ( 2 , 3 ) T {(5,4)^T,(2,3)^T} (5,4)T,(2,3)T
python代码实现
kd树代码-k近邻
import queue
import numpy as np
import heapq
import pandas as pd
'''kd树的结点类'''
class KDNode:
'''
kd树构造函数
:param dim: 结点分割的维度
:param value: 当前结点对应实例
:param label: 当前结点对应实例的类别
:param left: 结点左孩子
:param right: 结点右孩子
:param dist: 当前结点到目标点的距离
'''
def __init__(self, dim, value, label, left, right):
self.dim = dim
self.value = value
self.label = label
self.left = left
self.right = right
self.dist = 1.7976931348623157e+308 # 初始化为最大值,这个不重要,会被覆盖的
'''反着重写结点的比较函数,用于制造大根堆,因为heapq只能搞小根堆'''
def __lt__(self, other):
if self.dist>other.dist:
return True
else:
return False
'''kd树'''
class KDTree:
'''
初始化参数并生成kd树
其中实例和标签(类别)分别输入
:param values: 实例
:param labels: 类别
'''
def __init__(self, values, labels):
self.values = np.array(values)
self.labels = np.array(labels)
self.dim_len = len(self.values[0]) if len(self.values) > 0 else 0 # 特征向量的维度,命名避免与k近邻的k混淆
# 创建kd树
self.root = self.create_KDTree(self.values, self.labels, 0)
self.k = 0 # knn搜索个数
self.knn_heap = [] # 临时存放knn结果的堆,注意这里默认是小顶堆,下面要用相反数
'''
递归创建kd树
:param values: 实例
:param labels: 类别
:return: 该树的根节点
'''
def create_KDTree(self, values, labels, depth):
if len(labels) == 0:
return None
dim = depth % self.dim_len # 当前划分维度,注意这里不用+1,因为数组从0开始
# 对实例和类别按实例某特征排序,不懂可参考 http://t.csdn.cn/8ZItF
sort_index = values[:, dim].argsort()
values = values[sort_index]
labels = labels[sort_index]
mid = len(labels) // 2 # 双除号向下取整
node = KDNode(dim, values[mid], labels[mid], None, None)
node.left = self.create_KDTree(values[0:mid], labels[0:mid], depth + 1) # 递归创建左子树
node.right = self.create_KDTree(values[mid + 1:], labels[mid + 1:], depth + 1) # 递归创建右子树
return node
'''距离度量,这里使用欧氏距离'''
def dist(self, p1, p2):
return np.sqrt(np.sum((p1 - p2) ** 2))
"""
k近邻搜索的初始化
主要作用是对搜索进行兜底
:param target: 目标点
:param k: 需要搜索近邻点的数量
:return: 返回找到的实例和实例对应的标签组成的元组
"""
def search_KNN(self, target, k):
# 兜底
if self.root is None:
raise Exception('KD树不可为空')
if k > len(self.values):
raise ValueError('k值需小于等于实例数量')
if len(target) != len(self.root.value):
raise ValueError('目标点的维度和实例的维度大小需要一致')
# 初始化并开始搜索
self.k = k
self.knn_heap = []
self.search_KNN_core(self.root, target)
res_values = []
res_labels = []
# 将结果转换一下
for i in range(len(self.knn_heap)):
res_values.append(self.knn_heap[i].value)
res_labels.append(self.knn_heap[i].label)
# print(res_labels)
return (np.array(res_values),np.array(res_labels))
'''
k近邻搜索核心逻辑代码,由search_KNN调用
:param root: 当前便利到的结点
:param target: 目标点
'''
def search_KNN_core(self, node, target):
if node is None:
return []
value = node.value
dim = node.dim
# 先往其中一个区域搜索
if (target[dim] < value[dim]):
ath_child = node.right # 另一片区域对应结点
if node.left is not None:
self.search_KNN_core(node.left, target)
else:
ath_child = node.left # 另一片区域对应结点
if node.right is not None:
self.search_KNN_core(node.right, target)
# 处理本结点
node.dist = self.dist(value, target) # 结算本结点到目标节点的距离
# 判断是否需要更新堆
if len(self.knn_heap) < self.k: # 堆没满直接进堆
heapq.heappush(self.knn_heap, node)
else: # 堆若满则需要判断更新
fathest_node_in_k = heapq.heappop(self.knn_heap) # 已经找到的实例中距离目标点最远的实例
if node.dist < fathest_node_in_k.dist:
heapq.heappush(self.knn_heap, node)
else:
heapq.heappush(self.knn_heap, fathest_node_in_k)
if ath_child is not None:
fathest_node_in_k = heapq.heappop(self.knn_heap) # 获取堆顶供下面使用
heapq.heappush(self.knn_heap,fathest_node_in_k)
# 如果另一片区域与(以目标点为球心,以搜索到的集合中距离目标点最远的点到目标点的距离为半径)的超球体相交,则进入另一个子节点对应的区域搜索
# 如果堆没满,也进入另一篇区域
if len(self.knn_heap) < self.k or abs(ath_child.value[dim] - target[dim]) < fathest_node_in_k.dist:
self.search_KNN_core(ath_child, target)
'''先序输出,测试用'''
def print_KDTree(self):
stk = []
p = self.root
while len(stk) != 0 or p is not None:
# 走到子树最左边
while p is not None:
stk.append(p)
p = p.left
if len(stk) != 0:
cur_node = stk[len(stk) - 1]
stk.pop()
print(cur_node.value)
# 若有则进入右子树,进行新一轮循环
if cur_node.right is not None:
p = cur_node.right
# 一些测试的代码
# if __name__ == '__main__':
# # 创建kd树
# df = pd.DataFrame(pd.read_excel('./data/knn.xlsx'))
# values = df.values[:, :-1]
# labels = df.values[:, -1]
# kdtree = KDTree(values, labels)
# # kdtree.print_KDTree()
# kdtree.search_KNN([2.1,4.7], 5)
基于kd树的knn
真正用到knn还是用sklearn,这里只是写一下锻炼一下python
这个选k值的过程有点胡来,因为刚接触MLqaq
from statistics import mode
import numpy
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from sklearn.metrics import precision_score
from kd_tree import KDTree
plt.rcParams['font.sans-serif'] = ['SimHei']
class KNN:
def __init__(self, values, labels):
self.values = np.array(values)
self.labels = np.array(labels)
self.k = 1 # 初始化k值
self.min_correct_rate = 0.83 # 能接受的最小准确率,自行调整
self.train() # 训练出k值
self.kd_tree = KDTree(self.values, self.labels) # 创建全数据kd树
'''训练主要目的是为了选取k值'''
def train(self):
train_len = int(len(self.values) * 0.7) # 70%做训练集
# 训练集
train_values = self.values[:train_len]
train_labels = self.labels[:train_len]
# 验证集
verify_values = self.values[:train_len + 1]
verify_labels = self.labels[:train_len + 1]
# 创建kd树
self.kd_tree = KDTree(train_values, train_labels)
# 调参
correct_rate = 0
while correct_rate < self.min_correct_rate:
res_labels = self.predict(verify_values)
# 计算准确率
correct_rate = self.cal_correct_rate(verify_labels, res_labels)
self.k += 1
print("训练完成,验证集准确率为:{0},k为:{1}".format(correct_rate, self.k))
'''
knn入口
:param target: 目标点,一个或者多个
'''
def predict(self, target):
if target is None:
return
target = np.array(target)
shape = target.shape
if len(shape) == 1: # 只有一个实例
return self.predict_core(target)
else:
res = []
for i in range(shape[0]):
res.append(self.predict_core(target[i]))
res = np.array(res)
return res
'''
knn的核心方法
:param target: 这里target只能是一个实例
'''
def predict_core(self, target):
# 获取k个最邻近点对应的标签
knn_labels = self.kd_tree.search_KNN(target, self.k)[1]
# 取出k个点中最多的类别最为答案
return mode(knn_labels)
'''
precision_score老报错,自己写一个计算准确率
origin可以互换predict
'''
def cal_correct_rate(self, origin, predict):
Len = len(origin)
count = 0
for i in range(Len):
if origin[i] == predict[i]:
count += 1
return count / Len
if __name__ == '__main__':
# 读取数据
df = pd.DataFrame(pd.read_csv('./data/knn_data_2')) # 二维鸢尾花数据
# df = pd.DataFrame(pd.read_csv('./data/knn_data_3')) # 三维鸢尾花
values = df.values[:, :3]
labels = df.values[:, -1]
train_len = int(len(values) * 0.9)
# 测试集
test_values = values[:train_len]
test_labels = labels[:train_len]
# 训练集
train_values = values[:train_len + 1]
train_labels = labels[:train_len + 1]
# 二维数据下的散点图
# x1_min, x1_max = values[:, 0].min() - 0.5, values[:, 0].max() + 0.5 # 第一维坐标最大最小值
# x2_min, x2_max = values[:, 1].min() - 0.5, values[:, 1].max() + 0.5 # 第二维坐标最大最小值
# plt.scatter(values[:, 0], values[:, 1], c=labels, edgecolor="k")
# plt.xlim(x1_min, x1_max)
# plt.ylim(x2_min, x2_max)
# plt.xlabel("特征1")
# plt.ylabel("特征2")
# plt.show()
knn = KNN(train_values, train_labels)
res = knn.predict(test_values)
correct_rate = knn.cal_correct_rate(test_labels, res)
print('测试集预测准确率为:{}'.format(correct_rate))