Python实现CART决策树
CART决策树
- 前言
- 一、CART决策树算法
- 二、Python代码实现
-
- 1.计算结点GINI值
- 2.分离数据集
- 3.选择最好的特征
- 4.生成决策树
- 5.测试决策树
- 6.决策树可视化
- 7.主程序部分
- CART决策分类树所有代码
- 三、运行结果
- 总结
前言
CART算法的全称是Classification And Regression Tree,采用的是Gini指数(选Gini指数最小的特征s)作为分裂标准,是一种实用的分类算法。
一、CART决策树算法
主要思路是对一个数据集选择几个属性作为特征,对于每个特征提出一个划分条件,根据这个条件将结点分为两个子节点,对于子节点同样利用下一个特征进行划分,直到某结点的Gini值符合要求,我们认为这个结点的不纯性很小,该节点已成功分类。如此反复执行,最后可以得到由若干个结点组成的决策树,其中的每个叶节点都是分类的结果。
某结点的Gini值的计算公式如下:

如果要对某种划分计算Gini值,可以利用加权平均,即:
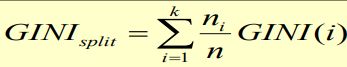
明确了Gini值的计算以及决策树的基本思路后,就可以继续向下看具体的代码实现了,本文没有使用sklearn库,如果读者只是需要使用该算法,而不想了解算法实际的实现思路的话,可以无需向下看了。
二、Python代码实现
主要分为6个步骤:
- 寻找到最佳属性
- 创建决策树
- 将上一结点分裂,分别计算左、右子节点的Gini值。
- 计算Gnin值有一种方法:将数据集对应这个属性的值排序,从头开始选择相邻两个值的平均值作为划分条件,计算该分发下的Gini值,如此遍历一遍,选出最小的一个Gini值对应的划分条件,作为该属性的最佳分裂条件
- 对于子节点,Gini值小于阈值,认为其是叶节点,结束这一方向的分裂。若Gini值大于阈值,认为分类还不够纯,需继续分裂,下一次分裂要使用不同的属性值。
- 递归调用创建决策树,就可以得到完整的决策树。
使用到的函数主要有5个:
- calcGini(dataSet) #计算结点GINI值
- splitDataSet(dataSet, n, value, type) #根据条件分离数据集
- FindBestFeature(dataSet) #选择最好的特征划分数据集,即返回最佳特征下标及传入数据集各列的Gini指数
- createTree(dataSet, features, decisionTree) #生成决策树。输入:训练数据集D,特征集A。输出:决策树T
- testTree(dataSet) #获得测试结果,给出混淆矩阵
1.计算结点GINI值
def calcGini(dataSet):
numTotal = dataSet.shape[0] # 记录本数据集总条数
length = len(dataSet[0]) # 计算特征列数
frequent_0 = 0.0 # 记录三种样本出现次数
frequent_1 = 0.0
frequent_2 = 0.0
for i in range(0,numTotal):
if dataSet[i][length-1] == '0.0':
frequent_0 += 1
elif dataSet[i][length-1] == '1.0':
frequent_1 += 1
elif dataSet[i][length-1] == '2.0':
frequent_2 += 1
gini = 1 - (frequent_0/numTotal)**2 - (frequent_1/numTotal)**2 - (frequent_2/numTotal)**2
return gini
2.分离数据集
def splitDataSet(dataSet, n, value, type):
subDataSet = []
numTotal = dataSet.shape[0] # 记录本数据集总条数
if type == 1: # type==1对应小于等于value的情况
for i in range(0,numTotal):
if float(dataSet[i][n]) <= value:
subDataSet.append(dataSet[i])
elif type == 2: # type==2对应大于value的情况
for i in range(0,numTotal):
if float(dataSet[i][n]) > value:
subDataSet.append(dataSet[i])
subDataSet = np.array(subDataSet) # 强制转换为array类型
return subDataSet,len(subDataSet)
3.选择最好的特征
def FindBestFeature(dataSet):
numTotal = dataSet.shape[0] # 记录本数据集总条数
numFeatures = len(dataSet[0]) - 2 # 计算特征列数
bestFeature = -1 # 初始化参数,记录最优特征列i,下标从0开始
columnFeaGini={} # 初始化参数,记录每一列x的每一种特征的基尼 Gini(D,A)
for i in range(1, numFeatures+1): # 遍历所有x特征列,i为特征标号
featList = list(dataSet[:, i]) # 取这一列x中所有数据,转换为list类型
featListSort = [float(x) for x in featList]
featListSort.sort() # 对该特征值排序
FeaGinis = []
FeaGiniv = []
for j in range(0,len(featListSort)-1): # j为第几组数据
value = (featListSort[j]+featListSort[j+1])/2
feaGini = 0.0
subDataSet1,sublen1 = splitDataSet(dataSet, i, value, 1) # 获取切分后的数据
subDataSet2,sublen2 = splitDataSet(dataSet, i, value, 2)
feaGini = (sublen1/numTotal) * calcGini(subDataSet1) + (sublen2/numTotal) * calcGini(subDataSet2) # 计算此分法对应Gini值
FeaGinis.append(feaGini) # 记录该特征下各种分法遍历出的Gini值
FeaGiniv.append(value) # 记录该特征下的各种分法
columnFeaGini['%d_%f'%(i,FeaGiniv[FeaGinis.index(min(FeaGinis))])] = min(FeaGinis) # 将该特征下最小的Gini值
bestFeature = min(columnFeaGini, key=columnFeaGini.get) # 找到最小的Gini指数对应的数据列
return bestFeature,columnFeaGini
4.生成决策树
def createTree(dataSet, features, decisionTree):
if len(features) > 2: #特征未用完
bestFeature, columnFeaGini = FindBestFeature(dataSet)
bestFeatureLable = features[int(bestFeature.split('_')[0])] # 最佳特征
NodeName = bestFeatureLable + '\n' +'<=' + bestFeature.split('_')[1] #结点名称
decisionTree = {NodeName: {}} # 构建树,以Gini指数最小的特征bestFeature为子节点
else:
return decisionTree
LeftSet, LeftSet_len = splitDataSet(dataSet, int(bestFeature.split('_')[0]), float(bestFeature.split('_')[1]), 1)
RightSet, RightSet_len = splitDataSet(dataSet, int(bestFeature.split('_')[0]), float(bestFeature.split('_')[1]), 2)
del (features[int(bestFeature.split('_')[0])]) # 该特征已为子节点使用,则删除,以便接下来继续构建子树
if calcGini(LeftSet) <= 0.1 or len(features) == 2:
L_lables_grp = dict(Counter(LeftSet[:,-1]))
L_leaf = max(L_lables_grp, key=L_lables_grp.get) # 获得划分后出现概率最大的分类作为结点的分类
decisionTree[NodeName]['Y'] = L_leaf # 设定左枝叶子值
elif calcGini(LeftSet) > 0.1:
dataSetNew = np.delete(LeftSet, int(bestFeature.split('_')[0]), axis=1) # 删除此最优划分x列,使用剩余的x列进行数据划分
L_subFeatures = features[:]
decisionTree[NodeName]['Y'] = {'NONE'}
decisionTree[NodeName]['Y'] = createTree(dataSetNew, L_subFeatures, decisionTree[NodeName]['Y']) #递归生成左边的树
if calcGini(RightSet) <= 0.1 or len(features) == 2:
R_lables_grp = dict(Counter(RightSet[:,-1]))
R_leaf = max(R_lables_grp, key=R_lables_grp.get) # 获得划分后出现概率最大的分类作为结点的分类
decisionTree[NodeName]['N'] = R_leaf # 设定右枝叶子值
elif calcGini(RightSet) > 0.1:
dataSetNew = np.delete(RightSet, int(bestFeature.split('_')[0]), axis=1) # 删除此最优划分x列,使用剩余的x列进行数据划分
R_subFeatures = features[:]
decisionTree[NodeName]['N'] = {'NONE'}
decisionTree[NodeName]['N'] = createTree(dataSetNew, R_subFeatures, decisionTree[NodeName]['N']) #递归生成右边的树
return decisionTree
5.测试决策树
def testTree(dataSet):
numTotal = dataSet.shape[0] # 记录本数据集总条数
testmemory = []
label = dataSet[:,-1]
TP = 0
FP = 0
TN = 0
FN = 0
for i in range(0,numTotal):
if float(dataSet[i][4]) <= 0.001444: #标准差
if float(dataSet[i][1]) <= 0.01022: #均值
if float(dataSet[i][6]) <= -0.589019: #峰度
testmemory.append('0.0')
else:
if float(dataSet[i][3]) <= -0.001811: #四分位差
if float(dataSet[i][2]) <= -0.000026: #中位数
testmemory.append('0.0')
else:
testmemory.append('2.0')
else:
if float(dataSet[i][2]) <= 0.007687: #中位数
if float(dataSet[i][5]) <= 0.452516: #偏度
testmemory.append('0.0')
else:
testmemory.append('0.0')
else:
testmemory.append('2.0')
else:
testmemory.append('2.0')
else:
if float(dataSet[i][3]) <= -0.013691: # 四分位差
testmemory.append('1.0')
else:
if float(dataSet[i][5]) <= 1.462280: #偏度
if float(dataSet[i][6]) <= -1.034223: # 峰度
if float(dataSet[i][1]) <= 0.009173: # 均值
if float(dataSet[i][2]) <= -0.004193: # 中位数
testmemory.append('2.0')
else:
testmemory.append('2.0')
else:
testmemory.append('0.0')
else:
testmemory.append('2.0')
else:
if float(dataSet[i][1]) <= -0.023631: # 均值
testmemory.append('2.0')
else:
testmemory.append('1.0')
for i in range(0, numTotal):
if (testmemory[i] == '1.0') and (label[i] == '1.0'):
TP += 1
elif (testmemory[i] == '1.0') and (label[i] != '1.0'):
FP += 1
elif (testmemory[i] != '1.0') and (label[i] != '1.0'):
TN += 1
elif (testmemory[i] != '1.0') and (label[i] == '1.0'):
FN += 1
print('TP:%d' % TP) #真阳性
print('FP:%d' % FP) #假阳性
print('TN:%d' % TN) #真阴性
print('FN:%d' % FN) #假阴性
cm = confusion_matrix(label, testmemory, labels=["0.0", "1.0", "2.0"])
plt.rc('figure', figsize=(5, 5))
plt.matshow(cm, cmap=plt.cm.cool) # 背景颜色
plt.colorbar() # 颜色标签
# 内部添加图例标签
for x in range(len(cm)):
for y in range(len(cm)):
plt.annotate(cm[x, y], xy=(y, x), horizontalalignment='center', verticalalignment='center')
plt.ylabel('True Label')
plt.xlabel('Predicted Label')
plt.title('decision_tree')
plt.savefig(r'confusion_matrix')
6.决策树可视化
可视化部分基本摘自《机器学习实战》第三章。
matplotlib.rcParams['font.family']='SimHei' # 用来正常显示中文
plt.rcParams['axes.unicode_minus']=False # 用来正常显示负号
decisionNode = dict(boxstyle="sawtooth", fc="0.8")
leafNode = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-")
def getNumLeafs(myTree):
numLeafs = 0
firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[
key]).__name__ == 'dict': # test to see if the nodes are dictonaires, if not they are leaf nodes
numLeafs += getNumLeafs(secondDict[key])
else:
numLeafs += 1
return numLeafs
def getTreeDepth(myTree):
maxDepth = 0
firstStr = list(myTree.keys())[0] # myTree.keys()[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[
key]).__name__ == 'dict': # test to see if the nodes are dictonaires, if not they are leaf nodes
thisDepth = 1 + getTreeDepth(secondDict[key])
else:
thisDepth = 1
if thisDepth > maxDepth: maxDepth = thisDepth
return maxDepth
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
xytext=centerPt, textcoords='axes fraction',
va="center", ha="center", bbox=nodeType, arrowprops=arrow_args)
def plotMidText(cntrPt, parentPt, txtString):
xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0]
yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1]
createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)
def plotTree(myTree, parentPt, nodeTxt): # if the first key tells you what feat was split on
numLeafs = getNumLeafs(myTree) # this determines the x width of this tree
# depth = getTreeDepth(myTree)
firstStr = list(myTree.keys())[0] # myTree.keys()[0] #the text label for this node should be this
cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.yOff)
plotMidText(cntrPt, parentPt, nodeTxt)
plotNode(firstStr, cntrPt, parentPt, decisionNode)
secondDict = myTree[firstStr]
plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD
for key in secondDict.keys():
if type(secondDict[
key]).__name__ == 'dict': # test to see if the nodes are dictonaires, if not they are leaf nodes
plotTree(secondDict[key], cntrPt, str(key)) # recursion
else: # it's a leaf node print the leaf node
plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW
plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD
def createPlot(myTree):
fig = plt.figure(1, facecolor='white')
fig.clf()
axprops = dict(xticks=[], yticks=[])
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) # no ticks
# createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses
plotTree.totalW = float(getNumLeafs(myTree))
plotTree.totalD = float(getTreeDepth(myTree))
plotTree.xOff = -0.5 / plotTree.totalW;
plotTree.yOff = 1.0;
plotTree(myTree, (0.5, 1.0), '')
plt.show()
7.主程序部分
trainingData, testingData= read_xslx(r'e:/Table/机器学习/1109/attribute_113.xlsx')
features = list(trainingData[0]) # x的表头,即特征
trainingDataSet = trainingData[1:] # 训练集
bestFeature, columnFeaGini=FindBestFeature(trainingDataSet)
decisionTree = {}
decisiontree = createTree(trainingDataSet, features, decisionTree) # 建立决策树,CART分类树
print('CART分类树:\n', decisiontree)
testTree(testingData)
createPlot(decisiontree)
CART决策分类树所有代码
# -*- coding: utf-8 -*- 支持文件中出现中文字符
#########################################################################
"""
Created on Mon Nov 16 21:26:00 2020
@author: ixobgenw
代码功能描述: (1)计算结点GINI值
(2)分离数据集
(3)选择最好的特征
(4)生成决策树
(5)测试决策树
"""
#####################################################################
import xlrd
import numpy as np
from collections import Counter
import matplotlib.pyplot as plt
import matplotlib
#可视化部分
####################################################################################################################
matplotlib.rcParams['font.family']='SimHei' # 用来正常显示中文
plt.rcParams['axes.unicode_minus']=False # 用来正常显示负号
decisionNode = dict(boxstyle="sawtooth", fc="0.8")
leafNode = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-")
def getNumLeafs(myTree):
numLeafs = 0
firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[
key]).__name__ == 'dict': # test to see if the nodes are dictonaires, if not they are leaf nodes
numLeafs += getNumLeafs(secondDict[key])
else:
numLeafs += 1
return numLeafs
def getTreeDepth(myTree):
maxDepth = 0
firstStr = list(myTree.keys())[0] # myTree.keys()[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[
key]).__name__ == 'dict': # test to see if the nodes are dictonaires, if not they are leaf nodes
thisDepth = 1 + getTreeDepth(secondDict[key])
else:
thisDepth = 1
if thisDepth > maxDepth: maxDepth = thisDepth
return maxDepth
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
xytext=centerPt, textcoords='axes fraction',
va="center", ha="center", bbox=nodeType, arrowprops=arrow_args)
def plotMidText(cntrPt, parentPt, txtString):
xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0]
yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1]
createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)
def plotTree(myTree, parentPt, nodeTxt): # if the first key tells you what feat was split on
numLeafs = getNumLeafs(myTree) # this determines the x width of this tree
# depth = getTreeDepth(myTree)
firstStr = list(myTree.keys())[0] # myTree.keys()[0] #the text label for this node should be this
cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.yOff)
plotMidText(cntrPt, parentPt, nodeTxt)
plotNode(firstStr, cntrPt, parentPt, decisionNode)
secondDict = myTree[firstStr]
plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD
for key in secondDict.keys():
if type(secondDict[
key]).__name__ == 'dict': # test to see if the nodes are dictonaires, if not they are leaf nodes
plotTree(secondDict[key], cntrPt, str(key)) # recursion
else: # it's a leaf node print the leaf node
plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW
plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD
def createPlot(myTree):
fig = plt.figure(1, facecolor='white')
fig.clf()
axprops = dict(xticks=[], yticks=[])
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) # no ticks
# createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses
plotTree.totalW = float(getNumLeafs(myTree))
plotTree.totalD = float(getTreeDepth(myTree))
plotTree.xOff = -0.5 / plotTree.totalW;
plotTree.yOff = 1.0;
plotTree(myTree, (0.5, 1.0), '')
plt.show()
####################################################################################################################
#读取excel文件,70%为训练集,30%为测试集
####################################################################################################################
def read_xslx(xslx_path):
trainingdata = [] # 先声明一个空list
testingdata = []
data = xlrd.open_workbook(xslx_path) # 读取文件
table = data.sheet_by_index(0) # 按索引获取工作表,0就是工作表1
for i in range(int(0.7*table.nrows)): # table.nrows表示总行数
line = table.row_values(i) # 读取每行数据,保存在line里面,line是list
trainingdata.append(line) # 将line加入到trainingdata中,trainingdata是二维list
trainingdata = np.array(trainingdata) # 将trainingdata从二维list变成数组
for i in range(int(0.7*table.nrows),int(table.nrows)): # table.nrows表示总行数
line = table.row_values(i) # 读取每行数据,保存在line里面,line是list
testingdata.append(line) # 将line加入到testingdata中,testingdata是二维list
testingdata = np.array(testingdata) # 将testingdata从二维list变成数组
return trainingdata,testingdata
####################################################################################################################
#计算结点GINI值
####################################################################################################################
def calcGini(dataSet):
numTotal = dataSet.shape[0] # 记录本数据集总条数
length = len(dataSet[0]) # 计算特征列数
frequent_0 = 0.0 # 记录三种样本出现次数
frequent_1 = 0.0
frequent_2 = 0.0
for i in range(0,numTotal):
if dataSet[i][length-1] == '0.0':
frequent_0 += 1
elif dataSet[i][length-1] == '1.0':
frequent_1 += 1
elif dataSet[i][length-1] == '2.0':
frequent_2 += 1
gini = 1 - (frequent_0/numTotal)**2 - (frequent_1/numTotal)**2 - (frequent_2/numTotal)**2
return gini
####################################################################################################################
#根据条件分离数据集
####################################################################################################################
def splitDataSet(dataSet, n, value, type):
subDataSet = []
numTotal = dataSet.shape[0] # 记录本数据集总条数
if type == 1: # type==1对应小于等于value的情况
for i in range(0,numTotal):
if float(dataSet[i][n]) <= value:
subDataSet.append(dataSet[i])
elif type == 2: # type==2对应大于value的情况
for i in range(0,numTotal):
if float(dataSet[i][n]) > value:
subDataSet.append(dataSet[i])
subDataSet = np.array(subDataSet) # 强制转换为array类型
return subDataSet,len(subDataSet)
####################################################################################################################
#选择最好的特征划分数据集,即返回最佳特征下标及传入数据集各列的Gini指数
####################################################################################################################
def FindBestFeature(dataSet):
numTotal = dataSet.shape[0] # 记录本数据集总条数
numFeatures = len(dataSet[0]) - 2 # 计算特征列数
bestFeature = -1 # 初始化参数,记录最优特征列i,下标从0开始
columnFeaGini={} # 初始化参数,记录每一列x的每一种特征的基尼 Gini(D,A)
for i in range(1, numFeatures+1): # 遍历所有x特征列,i为特征标号
featList = list(dataSet[:, i]) # 取这一列x中所有数据,转换为list类型
featListSort = [float(x) for x in featList]
featListSort.sort() # 对该特征值排序
FeaGinis = []
FeaGiniv = []
for j in range(0,len(featListSort)-1): # j为第几组数据
value = (featListSort[j]+featListSort[j+1])/2
feaGini = 0.0
subDataSet1,sublen1 = splitDataSet(dataSet, i, value, 1) # 获取切分后的数据
subDataSet2,sublen2 = splitDataSet(dataSet, i, value, 2)
feaGini = (sublen1/numTotal) * calcGini(subDataSet1) + (sublen2/numTotal) * calcGini(subDataSet2) # 计算此分法对应Gini值
FeaGinis.append(feaGini) # 记录该特征下各种分法遍历出的Gini值
FeaGiniv.append(value) # 记录该特征下的各种分法
columnFeaGini['%d_%f'%(i,FeaGiniv[FeaGinis.index(min(FeaGinis))])] = min(FeaGinis) # 将该特征下最小的Gini值
bestFeature = min(columnFeaGini, key=columnFeaGini.get) # 找到最小的Gini指数对应的数据列
return bestFeature,columnFeaGini
####################################################################################################################
#生成决策树。输入:训练数据集D,特征集A。输出:决策树T
####################################################################################################################
def createTree(dataSet, features, decisionTree):
if len(features) > 2: #特征未用完
bestFeature, columnFeaGini = FindBestFeature(dataSet)
bestFeatureLable = features[int(bestFeature.split('_')[0])] # 最佳特征
NodeName = bestFeatureLable + '\n' +'<=' + bestFeature.split('_')[1] #结点名称
decisionTree = {NodeName: {}} # 构建树,以Gini指数最小的特征bestFeature为子节点
else:
return decisionTree
LeftSet, LeftSet_len = splitDataSet(dataSet, int(bestFeature.split('_')[0]), float(bestFeature.split('_')[1]), 1)
RightSet, RightSet_len = splitDataSet(dataSet, int(bestFeature.split('_')[0]), float(bestFeature.split('_')[1]), 2)
del (features[int(bestFeature.split('_')[0])]) # 该特征已为子节点使用,则删除,以便接下来继续构建子树
if calcGini(LeftSet) <= 0.1 or len(features) == 2:
L_lables_grp = dict(Counter(LeftSet[:,-1]))
L_leaf = max(L_lables_grp, key=L_lables_grp.get) # 获得划分后出现概率最大的分类作为结点的分类
decisionTree[NodeName]['Y'] = L_leaf # 设定左枝叶子值
elif calcGini(LeftSet) > 0.1:
dataSetNew = np.delete(LeftSet, int(bestFeature.split('_')[0]), axis=1) # 删除此最优划分x列,使用剩余的x列进行数据划分
L_subFeatures = features[:]
decisionTree[NodeName]['Y'] = {'NONE'}
decisionTree[NodeName]['Y'] = createTree(dataSetNew, L_subFeatures, decisionTree[NodeName]['Y']) #递归生成左边的树
if calcGini(RightSet) <= 0.1 or len(features) == 2:
R_lables_grp = dict(Counter(RightSet[:,-1]))
R_leaf = max(R_lables_grp, key=R_lables_grp.get) # 获得划分后出现概率最大的分类作为结点的分类
decisionTree[NodeName]['N'] = R_leaf # 设定右枝叶子值
elif calcGini(RightSet) > 0.1:
dataSetNew = np.delete(RightSet, int(bestFeature.split('_')[0]), axis=1) # 删除此最优划分x列,使用剩余的x列进行数据划分
R_subFeatures = features[:]
decisionTree[NodeName]['N'] = {'NONE'}
decisionTree[NodeName]['N'] = createTree(dataSetNew, R_subFeatures, decisionTree[NodeName]['N']) #递归生成右边的树
return decisionTree
####################################################################################################################
#获得测试结果
####################################################################################################################
def testTree(dataSet):
numTotal = dataSet.shape[0] # 记录本数据集总条数
testmemory = []
label = dataSet[:,-1]
TP = 0
FP = 0
TN = 0
FN = 0
for i in range(0,numTotal):
if float(dataSet[i][4]) <= 0.001444: #标准差
if float(dataSet[i][1]) <= 0.01022: #均值
if float(dataSet[i][6]) <= -0.589019: #峰度
testmemory.append('0.0')
else:
if float(dataSet[i][3]) <= -0.001811: #四分位差
if float(dataSet[i][2]) <= -0.000026: #中位数
testmemory.append('0.0')
else:
testmemory.append('2.0')
else:
if float(dataSet[i][2]) <= 0.007687: #中位数
if float(dataSet[i][5]) <= 0.452516: #偏度
testmemory.append('0.0')
else:
testmemory.append('0.0')
else:
testmemory.append('2.0')
else:
testmemory.append('2.0')
else:
if float(dataSet[i][3]) <= -0.013691: # 四分位差
testmemory.append('1.0')
else:
if float(dataSet[i][5]) <= 1.462280: #偏度
if float(dataSet[i][6]) <= -1.034223: # 峰度
if float(dataSet[i][1]) <= 0.009173: # 均值
if float(dataSet[i][2]) <= -0.004193: # 中位数
testmemory.append('2.0')
else:
testmemory.append('2.0')
else:
testmemory.append('0.0')
else:
testmemory.append('2.0')
else:
if float(dataSet[i][1]) <= -0.023631: # 均值
testmemory.append('2.0')
else:
testmemory.append('1.0')
for i in range(0, numTotal):
if (testmemory[i] == '1.0') and (label[i] == '1.0'):
TP += 1
elif (testmemory[i] == '1.0') and (label[i] != '1.0'):
FP += 1
elif (testmemory[i] != '1.0') and (label[i] != '1.0'):
TN += 1
elif (testmemory[i] != '1.0') and (label[i] == '1.0'):
FN += 1
print('TP:%d' % TP) #真阳性
print('FP:%d' % FP) #假阳性
print('TN:%d' % TN) #真阴性
print('FN:%d' % FN) #假阴性
cm = confusion_matrix(label, testmemory, labels=["0.0", "1.0", "2.0"])
plt.rc('figure', figsize=(5, 5))
plt.matshow(cm, cmap=plt.cm.cool) # 背景颜色
plt.colorbar() # 颜色标签
# 内部添加图例标签
for x in range(len(cm)):
for y in range(len(cm)):
plt.annotate(cm[x, y], xy=(y, x), horizontalalignment='center', verticalalignment='center')
plt.ylabel('True Label')
plt.xlabel('Predicted Label')
plt.title('decision_tree')
plt.savefig(r'confusion_matrix')
####################################################################################################################
trainingData, testingData= read_xslx(r'e:/Table/机器学习/1109/attribute_113.xlsx')
features = list(trainingData[0]) # x的表头,即特征
trainingDataSet = trainingData[1:] # 训练集
bestFeature, columnFeaGini=FindBestFeature(trainingDataSet)
decisionTree = {}
decisiontree = createTree(trainingDataSet, features, decisionTree) # 建立决策树,CART分类树
print('CART分类树:\n', decisiontree)
testTree(testingData)
createPlot(decisiontree)
三、运行结果
CART分类树:
{‘标准差\n<=0.001444’: {‘Y’: {‘均值\n<=0.010220’: {‘Y’: {‘峰度\n<=-0.589019’: {‘Y’: ‘0.0’, ‘N’: {‘四分位差\n<=-0.001811’: {‘Y’: {‘中位数\n<=-0.000026’: {‘Y’: ‘0.0’, ‘N’: ‘2.0’}}, ‘N’: {‘中位数\n<=0.007687’: {‘Y’: {‘偏度\n<=0.452516’: {‘Y’: ‘0.0’, ‘N’: ‘0.0’}}, ‘N’: ‘2.0’}}}}}}, ‘N’: ‘2.0’}}, ‘N’: {‘四分位差\n<=-0.013691’: {‘Y’: ‘1.0’, ‘N’: {‘偏度\n<=1.462280’: {‘Y’: {‘峰度\n<=-1.034223’: {‘Y’: {‘均值\n<=0.009173’: {‘Y’: {‘中位数\n<=-0.004193’: {‘Y’: ‘2.0’, ‘N’: ‘2.0’}}, ‘N’: ‘0.0’}}, ‘N’: ‘2.0’}}, ‘N’: {‘均值\n<=-0.023631’: {‘Y’: ‘2.0’, ‘N’: ‘1.0’}}}}}}}}
 混淆矩阵:
混淆矩阵:
如果将“1”看做一类,“0”和“2”看做一类,结果为:
TP:13
FP:0
TN:74
FN:3
