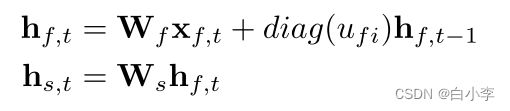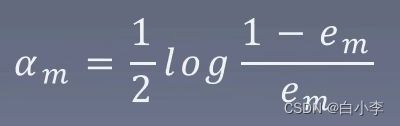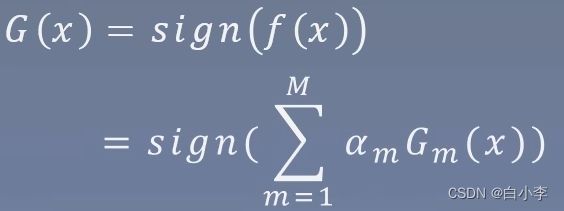2022/11/20周报

目录

文献阅读

1、题目和摘要

2、问题的提出

3、梯度时间反向传播以及解决梯度消失和消除问题

4、与单层RNN比较

5、网络结构和实验

深度学习（提升方法）

1、提升方法的基本思路

2、Bagging和Boosting

3、AdaBoost

文献阅读

1、题目和摘要

独立递归神经网络 (IndRNN): 构建更长更深的RNN

2、问题的提出

递归神经网络在处理序列数据方面得到了广泛的应用。 然而，由于重复权重的重复算法，RNNs普遍存在梯度消失和爆炸问题，并且难以学习长期模式，因此很难训练RNNs。 长短时记忆(LSTM)和门控循环单元(GRU)是为了解决这些问题而发展起来的，但双曲正切和sigmoid作用函数的使用导致了分层的梯度衰减。因此，构建一个高效可训练的深度网络是非常需要的。除此之外，现有的RNN模型具有相同的组合，其中反复出现的连接缠绕着所有的神经元。这使得解释和理解训练神经元的角色变得困难。

IndRNN的优点：

1、梯度随时间的反向传播可以有效地解决梯度消失和爆炸问题。

2、由于各层神经元的独立性，各层INDRNN神经元的行为易于解释。

3、使用IndRNN可以保持长时记忆，以处理长序列。实验证明，INDRNN可以很好地处理5000步以上的序列，而LSTM只能处理小于1000步的序列。

4、IndRNN能以RELU等非饱和函数作为激活函数，训练健壮。

5、多层IndRNN可以有效地堆叠，尤其是在层上有剩余连接的情况下，以增加网络的深度。

3、梯度时间反向传播以及解决梯度消失和消除问题

对于每一层中的梯度反向传播，由于在一层中神经元之间没有相互作用，因此IndRNN的梯度可以由每一个神经元间接计算。

梯度仅涉及可以容易调节的标量值un的指数项，而激活函数的梯度通常在一定范围内。与普通RNN相比，IndRNN的梯度直接取决于循环权重的值，而不是矩阵积。因此，IndRNN的训练比传统的RNN具有更强的鲁棒性。

 

对于解决梯度随时间的爆炸和消失问题，我们只需要调节指数项到适当的范围

 特别是对于多层RNN，具有relu激活功能的循环权重范围的约束可以放宽到|Un| ∈ [0,(T−t)√γ]。当重复权重为0时，神经元只使用当前输入的信息，而不保留过去的任何信息。 这样，不同的神经元就可以学习保持不同长度的记忆。

4、与单层RNN比较

将两层IndRNN与传统的单层RNN进行了比较。为简单起见，IndRNN和传统RNN都忽略了偏差项。假设一个简单的N神经元两层网络，其中第二层的递归权重为零，这意味着第二层只是随时间共享的完全连接的层。

两层IndRNN的第一层和第二层可以是分别由 以下 两个公式表示。

 这仅施加了递归权重 (U) 可对角化的约束。因此，简单的两层IndRNN网络可以表示具有可对角化递归权重 (U) 的传统RNN网络。换句话说，在线性激活下，具有可对角化递归权重 (U) 的传统RNN是两层IndRNN的特例，其中第二层的递归权重为零，而第二层的输入权重是可逆的。

尽管各层IndRNN神经元之间是相互独立的，但多层IndRNN能很好地表达跨通道信息。

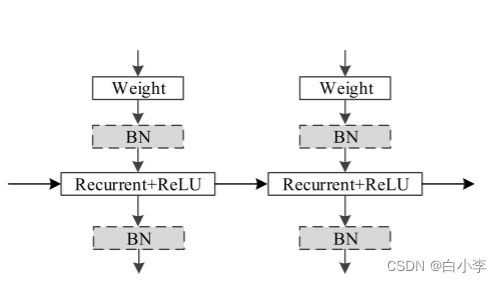
5、网络结构和实验

其中“weight”和“Recurrent+Relu”表示输入的过程和以Relu为激活函数的每一步的循环过程。 通过堆叠这个基本架构，可以构建一个深度的INDRNN网络。 使用sigmoid和双曲正切函数衰减层上梯度的基于LSTM的体系结构相比，非饱和激活函数 (例如remu) 减少了层上的梯度消失问题。此外，在IndRNN网络中，也可以在激活功能之前或之后使用以 “BN” 表示的批归一化。

 实验采用加法问题进行评估模型

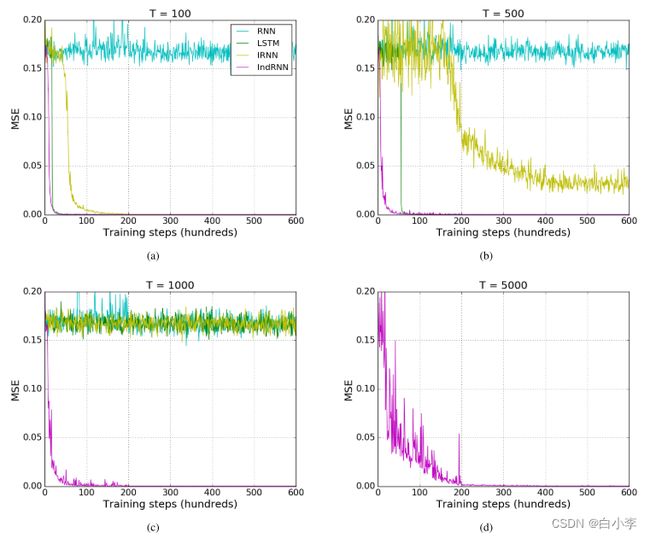
在（a）、（b）、（c）看出对于短序列(t=100)，大多数模型（带有TANH的前Cept RNN）表现良好，因为它们收敛到一个非常小的误差（比基线小得多）。 当序列长度增加时，IRNN模型和LSTM模型收敛困难，当序列长度达到1000时，RNN模型和LSTM模型不再能够最小化误差。 然而，所提出的IndRNN仍然可以很快收敛到一个小误差。 这表明，与传统的RNN和LSTM相比，所提出的INDRNN可以对更长时间的记忆进行建模。

对（d）看普通的RNN和LSTM只能保持一个中等范围的内存（大约500-1000个时间步）。 为了评价所提出的IN-DRNN模型对非常长时记忆的影响，在图进行了长度为5000的序列实验 2(d).可以看出，IndRNN仍然可以很好地对其进行建模。

 文章本文提出了一种独立递归神经网络(INDRNN)，其中一层神经元之间是相互独立的。 解释了IndRNN在时间 过程中的梯度反向传播，提出了一种有效地解决梯度消失和爆炸问题的调节技术。 与现有的RNN模型包括LSTM和GRU相比，InDRNN可以处理更长的时间序列。将基本的INDRNN堆叠起来构造深层网络，特别是结合层上的残差约束，对深层网络进行快速训练。 此外，每一层神经元之间的独立性允许更好地解释神经元。多个基本任务的实验验证了所提出的INDRNN相对于现有RNN模型的优势。

深度学习（提升方法）

1、提升方法的基本思路

将弱可学习算法提升为强可学习算法，其中提升方法是集成学习的一种。

所谓弱可学习，是指学习的正确率仅略优于随机猜测的多项式学习算法；强可学习指正确率较高的多项式学习算法。集成学习的泛化能力一般比单一的基分类器要好，这是因为大部分基分类器都分类错误的概率远低于单一基分类器的。

集成学习的主要类别：序列方法和并行方法。

Bagging和Boosting都是将已有的分类或回归算法通过一定方式组合起来，形成一个性能更加强大的分类器，更准确的说这是一种分类算法的组装方法，即将弱分类器组装成强分类器的方法。

2、Bagging和Boosting

在训练集上：

Bagging：每个训练集都是从原始训练集中有放回的选取出来的，每个训练集各不相同且相互独立。

Boosting：每一轮的训练集不变，只是训练集中每个样例在分类器中的权重发生变化。而权值是根据上一轮的分类结果进行调整。

在样本权值上：

Bagging：使用均匀取样，每个样例的权重相等。

Boosting：根据每一轮的训练不断调整权值，分类错误的样本拥有更高的权值。

在所使用的预测函数上(弱分类器)：

Bagging：所有预测函数的权重相等。

Boosting：每个弱分类器都有相应的权重，对于分类误差小的分类器会有更大的权重。

在并行计算上：

Bagging：各个预测函数可以并行生成，数据集、模型独立，没有系列关系

Boosting：各个预测函数只能顺序生成，后一个模型需要前一个模型的参数结果。

这两种方法都是把若干个分类器整合为一个分类器的方法，通过不同的整合方式，得到不同的效果，将不同的分类算法套入到此类算法框架中一定程度上会提高了原单一分类器的分类效果，提升了原有算法的性能，但是也增大了计算量。

3、AdaBoost

算法步骤：

1）初始化训练数据的权值分布

 2）对m=1，2····，M

a)使用具有权值分布Dm的训练数据集学习，得到基本分类器

Gm(x) : X->{-1, +1}

b)计算Gm(x)在训练数据集上的分类误差率

 

c)计算Gm(x)在训练数据集上的分类误差

 d)更新训练数据集的权值分布，Zm是规范化因子，它使D(m+1)成为一个概率分布。

 （3）构建基本分类器的先行组合

 

得到最终分类器