【机器学习】主成分分析

有任何的书写错误、排版错误、概念错误等，希望大家包含指正。

维数灾难

在高维情形下出现的数样本稀疏、距离计算困难等问题，是所有机器学习方法共同面临的的严重障碍，被称为“维数灾难”或“维数危机”（curse of dimensionality）。

为了方便思考，我们对离散属性（样本特征）进行分析。属性 $a_1$ 的可选值数量为 $10$ 个，那么想要覆盖整个由 $a_1$ 构成的属性空间，需要 $10$ 个在属性 $a_1$ 取值不同的样本即可；增加一个可选值数量同样为 $10$ 的属性 $a_2$，此时属性空间是由 $a_1$ 和 $a_2$ 构成的二维空间，需要 $10^2$ 个在属性 $a_1$ 或属性 $a_2$ 上取值不同的样本。故，对于 $d$ 维属性空间，需要的样本个数为 $10^d$ ，显然覆盖整个属性空间的样本个数是随着维度增加而指数级增长的。

所需样本的个数增长是迅速的，但是实际我们能够拥有的训练样本数量相对较少的，导致训练样本在属性空间中的分布是稀疏的，也更容易找到一个超平面将训练样本分开。因为随着属性数量趋向于无限大，样本密度非常稀疏，训练样本被分错的可能性趋向于零。当我们将高维空间的分类结果映射到低维空间时，会出现一个严重的问题，样本几乎被非线性分类器完美分类，低维中的分类决策面变得非常复杂，甚至出现单个样本与其他样本被决策面隔开的情况，这就是我们常说的“过拟合”现象（over-fitting）。

缓解维数灾难的两个重要途径是降维（dimension reduction）和特征选择（feature selection）。其中降维一般是通过某种数学变换将原始高维属性空间转变为一个低维“子空间”，在这个子空间中样本密度大幅提高，距离计算也变得更为容易。之所以可以进行降维操作，是因为很多时候，人们观测或收集到的数据样本虽然是高维的，但与学习任务密切相关的也许仅是某个低维分布，即高维空间中的一个低维“嵌入”（embedding）。可以理解为尽管观测样本的属性非常多，但是仅需其中的少量属性就可以训练出最佳分类器或预测器。

下面我们将介绍降维中的经典算法，主成分分析（Principal Component Analysis，PCA）。

主成分分析

主成分分析的主要思想是，首先对给定样本进行中心化，使得样本的每一个属性的均值变为 $0$。之后对样本进行正交变换，原来由线性相关变量表示的样本，通过正交变换变成若干个线性无关的新（抽象）属性表示的样本。新属性是可能的正交变换中原属性的方差和（信息保存）最大的，方差表示在新属性上信息的大小。。将新变量依次称为第一主成分、第二主成分等。这就是主成分分析的基本思想。通过主成分分析，可以利用主成分近似地表示原始数据，这可理解为发现数据的"基本结构" ；也可以把数据由少数主成分表示，这可理解为对数据降维。

注意：

主成分分析的第一步，也可以选择对原始数据进行标准化，而不是中心化，下面公式的推导采用的是中心化；

原样本经过正交变换后，得到的新属性一般是没有具体含义的，或者是我们无法用语言理解的，故称为抽象属性；

在信息论中，数据越混乱提供的信息越多，因为方差是对变量混乱程度的表达，所以方差越大，保留的信息量越大；

降维是通过选出几个主成分来实现的，如果选出全部主成分就起不到我们想要的降维效果了。

几何解释

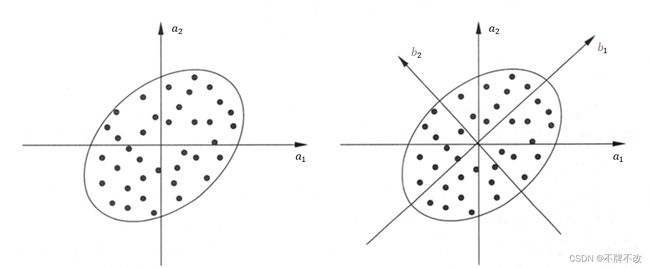
下面给出主成分分析的直观解释。假设存在一些二维样本，对这些样本进行进行中心化（或规范化）后如图 $1$ 左子图所示。主成分分析希望找到若干正交坐标轴，使样本在新坐标系下的方差尽可能大。对比图 $1$ 右子图的 $b_1$ 轴和 $b_2$ 轴，显然将样本投影到 $b_2$ 轴比投影到 $b_1$ 轴更加聚集，保留的信息也就更少。极端一点来理解，如果样本投影到 $b_1$ 轴没有发生任何重叠，但是投影到 $b_2$ 轴的样本完全重叠成一个点，对比两种投影方式，想要通过投影后的样本恢复得到原始样本信息，用投影到 $b_1$ 轴的样本进行恢复会更加准确。

当然，在选取投影面（轴）时不能仅仅对比 $b_1$ 和 $b_2$ 两个轴，而是从全部可能的轴中选择最佳的轴。 从下图中可以看到我们认为 $b_1$ 是最佳的轴，获取到的第一个轴 $b_1$ 被称为第一主成分。接下来是确定第二、三、…… 主成分，次主属性要在保证与前面全部主成分正交的前提下投影方差最大，之所以要求正交，是因为希望新属性线性无关。对于图 $1$ 的二维样本而言，确定了第一主成分 $b_1$ 后，只能选择唯一的与 $b_1$ 正交的 $b_2$ 作为第二主成分，且仅包括这两个主成分。

图 1    主成分分析的示例

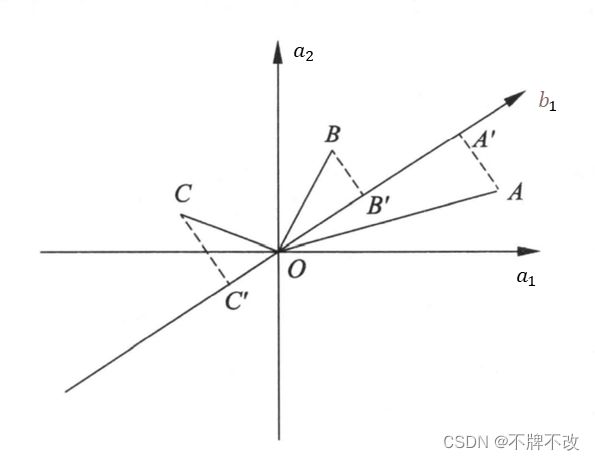
再看看最大方差的几何解释。假设有两个属性 $a_1$ 和 $a_2$，三个样本点 $A$、$B$ 和 $C$，样本分布在由 $a_1$ 和 $a_2$ 组成的坐标系中，如图 $2$ 所示。对坐标系进行旋转变换，得到新的坐标轴 $b_1$，表示新的属性 $b_1$。样本点 $A$、$B$、$C$ 在 $b_1$ 轴上投影，得到 $b_1$ 轴的坐标值 $A^{\prime }$、$B^{\prime }$、$C^{\prime }$。坐标值的平方和 $O{A}^{\prime 2}+O{B}^{\prime 2}+O{C}^{\prime 2}$ 表示样本在新属性上的方差和。主成分分析旨在选取正交变换中方差最大的变量，作为第一主成分， 也就是旋转变换中坐标值的平方和最大的轴。注意到旋转变换中样本点到原点的距离的平方和 $O{A}^2+O{B}^2+O{C}^2$ 保持不变，根据勾股定理，坐标值的平方和 $O{A}^{\prime 2}+O{B}^{\prime 2}+O{C}^{\prime 2}$ 最大等价于样本点到 $b_1$ 轴的距离的平方和 $A{A}^{\prime 2}+B{B}^{\prime 2}+C{C}^{\prime 2}$ 最小。所以，等价地， 主成分分析在旋转变换中选取离样本点的距离平方和最小的轴，作为第一主成分。第二主成分等的选取，在保证与己选坐标轴正交的条件下，类似地进行。

因为已经对原坐标系下的样本进行了中心化，所以在计算投影后样本在 $b_1$ 上的方差时，无需再进行中心化，此时的坐标值已经是中心化后的值了，故直接平方再累加就是样本方差。具体证明也非常简单，不再展示。

严谨的来说，样本方差的平方项系数应该为 $\frac{1}{n-1}$，数据总体方差的平方项系数应该为 $\frac{1}{n}$，但是我们有时候会忽略系数，并且讨论”数据总体“而不是”样本“，这些约定都是为了方便处理和理解，所以见到忽略系数的方差也不要差异，它们只是相差一个倍数。

图 2    主成分的几何解释

两个角度

上面仅从几何角度解释了 PCA 的思想，接下来我们从”最大投影方差“和”最小重构代价“两个角度来介绍数学推导。

首先我们规定常用符号。数据集 $D=\{(x_1,y_1),(x_2,y_2),\dots ,(x_n,y_n)\}$，向量 $x_i\in {\mathbb{R}}^p$ 为样本，$y_i\in \mathbb{R}$ 为标签，$i=1,2,\dots ,n$；$W\in {\mathbb{R}}^p$ 为模型参数（权重）。

记
$$\begin{gathered} X={\left(\begin{array}{cccc}{x}_1& x_2& \dots & x_n\end{array}\right)}^T=\left(\begin{array}{c}{x}_1^T\\ x_2^T\\ ⋮\\ x_n^T\end{array}\right)={\left(\begin{array}{cccc}{x}_{11}& x_{12}& \dots & x_{1p}\\ x_{21}& x_{22}& \dots & x_{2p}\\ ⋮& ⋮& & ⋮\\ x_{n1}& x_{n2}& \dots & x_{np}\end{array}\right)}_{n\times p} \\ Y={\left(\begin{array}{cccc}{y}_1& y_2& \dots & y_n\end{array}\right)}_{n\times 1}^T \end{gathered}$$

令
$$1_n=\left(\begin{array}{c}1\\ 1\\ ⋮\\ 1\end{array}\right)$$
那么，样本均值可以表示为
$$\begin{array}{rl}{\bar{X}}_{p\times 1}& =\frac{1}{n}\sum _{i=1}^n{x}_i\\ & =\frac{1}{n}\left(\begin{array}{cccc}{x}_1& x_2& \dots & x_n\end{array}\right)\left(\begin{array}{c}1\\ 1\\ ⋮\\ 1\end{array}\right)\\ & =\frac{1}{n}{X}^T{1}_n\end{array}$$
样本方差（协方差矩阵）表示为
$$\begin{array}{rl}{S}_{p\times p}& =\frac{1}{n}\sum _{i=1}^n(x_i-\bar{X})(x_i-\bar{X}{)}^T\\ & =\frac{1}{n}\left(\begin{array}{cccc}{x}_1-\bar{X}& x_2-\bar{X}& \dots & x_n-\bar{X}\end{array}\right)\left(\begin{array}{c}(x_1-\bar{X}{)}^T\\ (x_2-\bar{X}{)}^T\\ ⋮\\ (x_n-\bar{X}{)}^T\end{array}\right)\\ & =\frac{1}{n}(\left(\begin{array}{cccc}{x}_1& x_2& \dots & x_n\end{array}\right)-\bar{X}{1}_n^T)(\left(\begin{array}{c}{x}_1^T\\ x_2^T\\ ⋮\\ x_n^T\end{array}\right)-1_n{\bar{X}}^T)\\ & =\frac{1}{n}(X^T-\bar{X}{1}_n^T)(X-1_n{\bar{X}}^T)\\ & =\frac{1}{n}(X^T-\frac{1}{n}{X}^T{1}_n{1}_n^T)(X-\frac{1}{n}{1}_n{1}_n^{T}X)\\ & =\frac{1}{n}{X}^T(I_n-\frac{1}{n}{1}_n{1}_n^T)(I_n-\frac{1}{n}{1}_n{1}_n^T)X\end{array}$$
令
$$H=I_n-\frac{1}{n}{1}_n{1}_n^T$$

矩阵 $H$ 称为中心化矩阵，其作用是通过数据左乘 $H$ 实现将一组数据中心化，即 $HX$ 。

矩阵 $H$ 具有如下性质：

1. $H^T=(I_n-\frac{1}{n}{1}_n{1}_n^T{)}^T=(I_n-\frac{1}{n}{1}_n{1}_n^T)=H$
2. $H^2=H$

证明：
$$\begin{array}{rl}{H}^2& =(I_n-\frac{1}{n}{1}_n{1}_n^T)(I_n-\frac{1}{n}{1}_n{1}_n^T)\\ & =I_n-\frac{2}{n}{1}_n{1}_n^T+\frac{1}{n^2}{1}_n{1}_n^T{1}_n{1}_n^T\end{array}$$
其中 $1_n{1}_n^T{1}_n{1}_n^T=1_n(1_n^T{1}_n)1_n^T=n{1}_n{1}_n^T$ 为元素全是 $n$ 的矩阵

可得
$$\begin{gathered} \frac{1}{n^2}{1}_n{1}_n^T{1}_n{1}_n^T=\frac{1}{n}\left(\begin{array}{cccc}1& 1& \dots & 1\\ 1& 1& \dots & 1\\ ⋮& ⋮& & ⋮\\ 1& 1& \dots & 1\end{array}\right) \\ \frac{2}{n}{1}_n{1}_n^T=\frac{2}{n}\left(\begin{array}{cccc}1& 1& \dots & 1\\ 1& 1& \dots & 1\\ ⋮& ⋮& & ⋮\\ 1& 1& \dots & 1\end{array}\right) \end{gathered}$$
故
$$H^2=I_n-\frac{1}{n}\left(\begin{array}{cccc}1& 1& \dots & 1\\ 1& 1& \dots & 1\\ ⋮& ⋮& & ⋮\\ 1& 1& \dots & 1\end{array}\right)=I_n-\frac{1}{n}{1}_n{1}_n^T=H$$

将 $H$ 代入 $S$ 中得
$$S=\frac{1}{n}{X}^{T}HHX=\frac{1}{n}{X}^{T}HX$$

最大投影方差

上面提到 PCA 是希望找到方差最大的投影面，假设我们要找的第一主成分为 $u_1$，满足 $||u_1|{|}_2=1$。将中心化后的样本 $x_i^{\prime }=x_i-\bar{X}$ 投影到 $u_1$ 上的值的含义为样本 $x^{\prime }$ 在轴 $u_1$ 上的分量或坐标值，即 $x^{\prime T}{u}_1$。对于已经中心化的数据来说，将投影后的数据依然是中心化的，那么投影后的这些样本在 $u_1$ 轴上坐标值的方差为 $\frac{1}{n}(x^{\prime T}{u}_1{)}^2$。

根据最大投影方差的思想，定义损失函数
$$\begin{gathered} J=\frac{1}{n}\sum _{i=1}^n((x_i-\bar{X}{)}^T{u}_1{)}^2 \\ s.t.u_1^T{u}_1=1 \end{gathered}$$
其中，$J$ 可以进一步变形
$$\begin{array}{rl}J& =\frac{1}{n}\sum _{i=1}^n((x_i-\bar{X}{)}^T{u}_1{)}^T((x_i-\bar{X}{)}^T{u}_1)\\ & =\frac{1}{n}\sum _{i=1}^n{u}_1^T(x_i-\bar{X})(x_i-\bar{X})u_1\\ & =u_1^T(\frac{1}{n}\sum _{i=1}^n(x_i-\bar{X})(x_i-\bar{X}{)}^T)u_1\\ & =u_1^{T}S{u}_1\end{array}$$
最大化投影后的方差就是最大化损失函数，所以
$$\begin{gathered} {\hat{u}}_1=\mathrm{a}\mathrm{r}\mathrm{g}\underset{u_1}{\max }{u}_1^{T}S{u}_1 \\ s.t.u_1^T{u}_1=1\text{\hspace{1em}(1)} \end{gathered}$$
定义拉格朗日函数
$$L(u_1,\lambda )=u_1^{T}S{u}_1+\lambda (1-u_1^T{u}_1)$$
对 $u_1$ 计算偏导，得
$$\frac{\partial L}{\partial u_1}=2S{u}_1-2\lambda u_1$$
令偏导等于 $0$，得
$$\begin{array}{rl}S{u}_1& =\lambda u_1\\ u_1^{T}S{u}_1& =\lambda \end{array}\text{\hspace{1em}(2)}$$
可见，$\lambda$ 为协方差矩阵 $S$ 的特征值，$u_1$ 既是特征向量也是第一主成分。式 $(1)$ 中的 $u_1^{T}S{u}_1$ 为我们要最大化的目标，亦式 $(2)$ 的左侧部分，因此最大的特征值 ${\lambda }_1$ 对应的特征向量 $u_1$ 为第一主成分。

接着求第二主成分 $u_2$，第二主成分不仅要保证 $||u_2|{|}_2=1$，而且需要满足与第一主成分正交，即 $u_2^T{u}_1=0$。对应式 $(1)$ 可得
$$\begin{gathered} {\hat{u}}_2=\mathrm{a}\mathrm{r}\mathrm{g}\underset{u_2}{\max }{u}_2^{T}S{u}_2 \\ s.t.u_2^T{u}_2=1,u_2^T{u}_1=0 \end{gathered}$$
定义拉格朗日函数
$$L(u_2,\lambda ,\varphi )=u_2^{T}S{u}_2+\lambda (1-u_2^T{u}_2)-\varphi u_2^T{u}_1$$

注意，此时 $u_1$ 已经计算出来了，是已知的。

对 $u_2$ 计算偏导，并令其等于 $0$，得
$$2S{u}_2-2\lambda u_2-\varphi u_1=0\text{\hspace{1em}(3)}$$
将方程左乘 $u_1^T$ 有
$$2u_1^{T}S{u}_2-2\lambda u_1^T{u}_2-\varphi u_1^T{u}_1=0$$
此式前两项为 $0$，且 $u_1^T{u}_1=1$，导出 $\varphi =0$，因此式 $(3)$ 变为
$$\begin{gathered} S{u}_2-\lambda u_2=0 \\ {u}_2^{T}S{u}_2=\lambda \end{gathered}$$
这与式 $(2)$ 类似，可以认为第二主成分为第二大特征值 ${\lambda }_2$ 对应的单位向量 $u_2$。

按照上面的方法我们可以递推的求得第一、第二、直到第 $p$ 主成分，分别为 $u_1$，$u_2$，$...$，$u_p$，对应协方差矩阵 $S$ 的按对应特征值从大到小排列的特征向量。并且，第 $k$ 主成分的方差等于 $S$ 的第 $k$ 个特征值。

整体看一下，对协方差矩阵进行特征值分解，分解得到的特征值表示样本投影到不同坐标轴上的方差，方差越大说明投影后样本的信息保留越完整，因此，我们可以选出最大的若干个特征值对应的特征向量作为坐标轴，将样本投影到新的低维坐标系中，从而实现降维。

最小重构代价

就像之前提到的，若投影后数据越分散，则重构越容易；若数据越集中，甚至重合到一个点，便很难重构回去。因此最小重构代价的思想也是在寻找投影后数据最分散的坐标轴。

中心化后的样本 $x_i^{\prime }=x_i-\bar{X}$，$x_i^{\prime }$ 在新坐标系中可以表示为每个坐标轴上的坐标值 $x_i^{\prime T}{u}_k$ 与标准基向量 $u_k$ 的乘积之和，即 $x_i^{\prime }={\sum }_{k=1}^p(x_i^{\prime T}{u}_k)u_k$ 。假设特征向量 $u_i$ 按照特征值 ${\lambda }_i$ 从大到小排列， $u_1$ 对应的 ${\lambda }_1$ 最大， $u_p$ 对应的 ${\lambda }_p$ 最小。我们将样本从 $p$ 维降至 $q(q<p)$ 维，则降维（重构）后的样本 ${\hat{x}}_i^{\prime }={\sum }_{k=1}^q(x_i^{\prime T}{u}_k)u_k$ 。

最小重构代价的思想是将降维后的 ${\hat{x}}_i^{\prime }$ 还原为 $x_i^{\prime }$ 所需代价最小，我们用二者的相似程度来度量代价，相似程度的度量方式为二范数平方。故，损失函数为
$$\begin{array}{rl}J& =\frac{1}{n}\sum _{i=1}^n||x_i^{\prime }-{\hat{x}}_i^{\prime }|{|}_2^2\\ & =\frac{1}{n}\sum _{i=1}^n||\sum _{k=1}^p(x_i^{\prime T}{u}_k)u_k-\sum _{k=1}^q(x_i^{\prime T}{u}_k)u_k|{|}_2^2\\ & =\frac{1}{n}\sum _{i=1}^n||\sum _{k=q+1}^p(x_i^{\prime T}{u}_k)u_k|{|}_2^2\end{array}$$
我们注意到 ${\sum }_{k=q+1}^p(x_i^{\prime T}{u}_k)u_k$ 是一个向量，可以理解为该向量是在标准正交基 $\{u_k\}(k=q+1,\dots ,p)$ 构成的坐标系中坐标为 $(x_i^{\prime T}{u}_{q+1},x_i^{\prime T}{u}_{q+2},\dots ,x_i^{\prime T}{u}_p)$ 的向量。在标准正交基下，对该向量求二范数的平方可以简化表示坐标值的平方和，即 $||{\sum }_{k=q+1}^p(x_i^{\prime T}{u}_k)u_k|{|}_2^2={\sum }_{k=q+1}^p(x_i^{\prime T}{u}_k{)}^2$ 。因此，损失函数变为
$$\begin{array}{rl}J& =\frac{1}{n}\sum _{i=1}^n\sum _{k=q+1}^p(x_i^{\prime T}{u}_k{)}^2\\ & =\sum _{k=q+1}^p\frac{1}{n}\sum _{i=1}^n(x_i^{\prime T}{u}_k{)}^2\\ & =\sum _{k=q+1}^p\frac{1}{n}\sum _{i=1}^n((x_i-\bar{X}{)}^T{u}_k{)}^2\\ & =\sum _{k=q+1}^p{u}_k^T(\frac{1}{n}\sum _{i=1}^n(x_i-\bar{X})(x_i-\bar{X}{)}^T)u_k\\ & =\sum _{k=q+1}^p{u}_k^{T}S{u}_k\end{array}$$
最佳投影面为
$$\begin{gathered} {\hat{u}}_k=\mathrm{a}\mathrm{r}\mathrm{g}\underset{u_k}{\min }\sum _{k=q+1}^p{u}_k^{T}S{u}_k \\ s.t.u_k^T{u}_k=1(k=q+1,q+2,\dots ,p) \end{gathered}$$
由于 $u_k$ 相互独立，因此可以转换为多个 $\mathrm{a}\mathrm{r}\mathrm{g}\min u_k^{T}S{u}_k$ 的带约束优化问题，对每一个优化问题单独求解
$$\begin{gathered} {\hat{u}}_k=\mathrm{a}\mathrm{r}\mathrm{g}\underset{u_k}{\min }{u}_k^{T}S{u}_k \\ s.t.u_k^T{u}_k=1 \end{gathered}$$
使用拉格朗日乘数法可以得到
$$u_k^{T}S{u}_k={\lambda }_k$$
其中，${\lambda }_k$ 表示协方差矩阵 $S$ 第 $k$ 大特征值。损失函数 $J$ 可以进一步化为
$$\begin{array}{rl}J& =\sum _{k=q+1}^p{u}_k^{T}S{u}_k\\ & =\sum _{k=q+1}^p{\lambda }_k\end{array}$$
这与“最大投影方差”中选出最大的 $q$ 个特征值对应的特征向量作为投影面类似，“最小重构代价”是丢弃最小的 $p-q$ 个特征值对应的特征向量，剩下的特征向量作为投影面，也就是对公式中最大化和最小化的理解。

算法流程

PCA 算法流程非常简洁。

$$\begin{array}{llccccccc}\text{输入:}& 样本集D=\{{x\text{x}x}_1,{x\text{x}x}_2,\cdot \cdot \cdot ,{x\text{x}x}_n\};& & & & & & & \\ & 低维空间维数q.& & & & & & & \\ \text{过程:}& & & & & & & & \end{array}$$

$$\begin{array}{rl}1:& 对所有样本进行中心化:x_i\leftarrow x_i-\frac{1}{n}{\sum }_{i=1}^n{x}_i;\\ 2:& 计算样本的协方差矩阵X{X}^T;\\ 3:& 对协方差矩阵X{X}^T做特征值分解;\\ 4:& 取最大的q个特征值所对应的特征向量u_1,u_2,\dots ,u_q\end{array}$$

$$\begin{array}{lcccccccc}\text{输出:}投影矩阵W=(u_1,u_2,\cdot \cdot \cdot ,u_k)& & & & & & & & \end{array}$$

算法 1    PCA 算法

其实也可以通过奇异值分解来实现 PCA 算法。首先，将数据 $X$ 中心化得到 $HX$，直接对 $HX$ 进行奇异值分解 $HX=U\Sigma V^T$。其中，$V$ 便是 PCA 算法中协方差矩阵 $S$ 的特征向量，${\Sigma }^T\Sigma$ 为特征值矩阵。

证明也非常简单。已知
$$S=\frac{1}{n}{X}^{T}HX$$
利用 $H$ 的对称性和幂等性，$S$ 进一步化为
$$\begin{array}{rl}S& =\frac{1}{n}{X}^T{H}^{T}HX\\ & =\frac{1}{n}(HX{)}^{T}HX\\ & =(U\Sigma V^T)U\Sigma V^T\\ & =V{\Sigma }^T{U}^{T}U\Sigma V^T\\ & =V{\Sigma }^T\Sigma V^T\end{array}$$
由于 ${\Sigma }^T\Sigma$ 为对角半正定矩阵，故
$$\begin{array}{rl}S& =V{\Sigma }^T\Sigma V^T\\ SV& =V({\Sigma }^T\Sigma )\\ SV& =({\Sigma }^T\Sigma )V\end{array}$$
可见，这与 PCA 中对协方差矩阵进行特征值分解等价。PCA 算法流程甚至可以减少至三步，当然，步数越少并不意味着效率更高，具体使用看具体场景。

主成分的个数

具体选择 $q$ 的方法，通常利用方差贡献率。记全部样本在原坐标系下第 $k$ 维分量，亦第 $k$ 维属性，为 $a_k$
$$a_k={\left(\begin{array}{c}{x}_{1k}\\ x_{2k}\\ ⋮\\ x_{nk}\end{array}\right)}_{n\times 1}$$
全部样本在第 $k$ 主成分的分量为 ${\hat{a}}_k$
$${\hat{a}}_k={\left(\begin{array}{c}{x}_1^T{u}_k\\ x_2^T{u}_k\\ ⋮\\ x_n^T{u}_k\end{array}\right)}_{n\times 1}$$
第 $q$ 主成分分量的方差贡献率定义为第 $q$ 个主成分分量的方差与所有方差之和的比，记作 ${\eta }_q$
$${\eta }_q=\frac{{\lambda }_q}{{\sum }_{i=1}^p{\lambda }_i}$$
其中，${\lambda }_k$ 表示协方差矩阵 $S$ 的第 $k$ 大特征值。

前 $q$ 个主成分分量的累计方差贡献率定义为 $q$ 个方差之和与所有方差之和的比
$$\sum _{i=1}^q{\eta }_i=\frac{{\sum }_{i=1}^q{\lambda }_i}{{\sum }_{i=1}^q{\lambda }_i}$$
通常取 $q$ 使得累计方差贡献率达到规定的百分比以上，例如 70%~80% 以上。累计方差贡献率反映了数据在主成分上保留信息的比例，但它不能反映对某个原有属性 $a_i$ 保留信息的比例，这时通常利用数据在前 $q$ 个主成分投影值对原有属性 $a_i$ 的贡献率。

这句话的含义为，累积方差贡献直接度量的是方差大小，即降维保留了多少主成分信息，但是主成分信息又不能与属性信息直接划等，因此度量属性信息的保留程度也非常有必要。

前 $q$ 个主成分分量 ${\hat{a}}_1,{\hat{a}}_2,\dots ,{\hat{a}}_q$ 对原有属性 $a_i$ 的贡献率定义为 $a_i$ 与 $({\hat{a}}_1,{\hat{a}}_2,\dots ,{\hat{a}}_q)$ 的相关系数的平方，记作 ${\mathcal{V}}_i$
$${\mathcal{V}}_i={\rho }^2(a_i,({\hat{a}}_1,{\hat{a}}_2,\dots ,{\hat{a}}_q))$$
计算公式为
$${\mathcal{V}}_i={\rho }^2(a_i,({\hat{a}}_1,{\hat{a}}_2,\dots ,{\hat{a}}_q))=\sum _{j=1}^q{\rho }^2(a_i,{\hat{a}}_j)$$
因为
$$\rho (a_i,{\hat{a}}_j)=\frac{\mathrm{c}\mathrm{o}\mathrm{v}(a_i,{\hat{a}}_j)}{\sqrt{\mathrm{v}\mathrm{a}\mathrm{r}(a_i)\mathrm{v}\mathrm{a}\mathrm{r}({\hat{a}}_j)}}=\frac{\mathrm{c}\mathrm{o}\mathrm{v}(X{e}_i,X{u}_j)}{\sqrt{{\sigma }_{ii}}\sqrt{{\lambda }_j}}$$
其中，$e_i$ 为基本单位向量，其第 $i$ 个分量为 $1$，其余为 $0$ ；${\sigma }_{ii}$ 表示协方差矩阵 $S$ 第 $i$ 行第 $i$ 列元素。再由协方差的性质
$$\mathrm{c}\mathrm{o}\mathrm{v}(X{e}_i,X{u}_j)=e_i^{T}S{u}_j={\lambda }_j{e}_i^T{u}_j={\lambda }_j{u}_{ij}$$
因此
$$\rho (a_i,{\hat{a}}_j)=\frac{\sqrt{{\lambda }_j}{u}_{ij}}{\sqrt{{\sigma }_{ii}}}$$
故 ${\mathcal{V}}_i$ 可以进一步变化为
$${\mathcal{V}}_i=\sum _{j=1}^q{\rho }^2(a_i,{\hat{a}}_j)=\sum _{j=1}^q\frac{{\lambda }_j{u}_{ij}^2}{{\sigma }_{ii}}$$
计算原有属性 $a_i$ 和降维后的 $q$ 个主成分分量的相关系数平方之和，可以感性地理解为，投影后每个分量都可能与原有属性存在一定的相关性，可能密切相关，可能完全无关，采用相关系数度量原有属性与每个分量的相关性，对它们平方求和，累积全部相关性作为对原有属性 $a_i$ 的保留程度。

REF

[1] 《统计学习方法（第二版）》李航著

[2] 《机器学习》周志华著

[3] 机器学习-降维 - bilibili

[4] 机器学习-白板推导系列(五)-降维（Dimensionality Reduction）笔记 - 知乎

[5] The Curse of Dimensionality in Classification