基于卷积神经网络的KBC
基于卷积神经网络的KBC
原文:
A Novel Embedding Model for Knowledge Base Completion Based on Convolutional Neural Network
摘要
本篇文章是将图片卷积的概念扩展并应用于知识图谱点的嵌入表示,简单来说,是对知识图谱中的每一个三元组组合而成的嵌入矩阵 ( v h , v r , v t ) ∈ R k × 3 , (v_h,v_r,v_t)\in R^{k \times 3}, (vh,vr,vt)∈Rk×3,k表示的是嵌入向量的维度,与不同的 1 × 3 1\times3 1×3的filters进行卷积运算,来提取嵌入三元组相同维度的关系。得到多个feature maps,然后将这些feature maps拼接在一起,得到三元组的一个嵌入向量表示,该嵌入表示在于一个权重向量做内积,得到的数值来对三元组进行打分,表示三元组的有效与否。
提出的方法
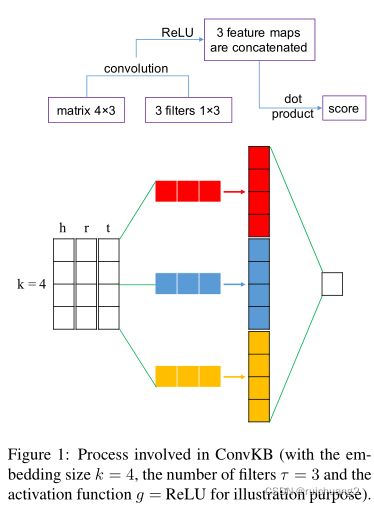
将知识图谱的三元组 ( v h , v r , v t ) (v_h,v_r,v_t) (vh,vr,vt)表示为矩阵的形式, A = [ v h , v r , v t ] ∈ R k × 3 A=[v_h,v_r,v_t] \in R^{k\times3} A=[vh,vr,vt]∈Rk×3,卷积核 ω ∈ R 1 × 3 \omega \in R^{1\times3} ω∈R1×3, ω \omega ω与A的每一行进行卷积运算,会得到一个k维的feature map,记为 v = [ v 1 , v 2 , . . . , v k ] ∈ R k v=[v_1,v_2,...,v_k]\in R_k v=[v1,v2,...,vk]∈Rk
v i = g ( ω ⋅ A i , : + b ) v_i=g(\omega \cdot A_{i,:}+b) vi=g(ω⋅Ai,:+b)
其中b是偏置项,g是激活函数。
用 Ω \Omega Ω和 τ = ∣ Ω ∣ \tau=|\Omega| τ=∣Ω∣分别表示卷积核集合和卷积核的个数。分别去和A进行卷积运算,运算结果直接拼接起来,得到一个向量 ∈ R τ k × 1 \in R^{\tau k \times 1} ∈Rτk×1,再和一个权重向量 w ∈ R τ k × 1 w\in R^{\tau k \times 1} w∈Rτk×1做内积运算,得到的值是对该三元组的打分:
f ( h , r , t ) = c o n c a t ( g ( [ v h , v r , v t ] × Ω ) ) T ⋅ w f(h,r,t)=concat(g([v_h,v_r,v_t]\times \Omega))^T\cdot w f(h,r,t)=concat(g([vh,vr,vt]×Ω))T⋅w
对于所有的三元组共享 Ω \Omega Ω和 w w w参数
最后,目标函数如下:
L = ∑ ( h , r , t ) ∈ G ∪ G ′ l o g ( 1 + e x p ( − l ( h , r , t ) ⋅ f ( h , r , t ) ) ) + λ 2 ∣ ∣ w ∣ ∣ 2 2 L=\sum_{(h,r,t) \in {G \cup G'}}log(1+exp(-l_(h,r,t) \cdot f(h,r,t)))+\frac{\lambda} {2} ||w||_2^2 L=(h,r,t)∈G∪G′∑log(1+exp(−l(h,r,t)⋅f(h,r,t)))+2λ∣∣w∣∣22
[1]: A Novel Embedding Model for Knowledge Base Completion Based on Convolutional Neural Network