R语言-基于集波士顿住房

1.使用数据集boston_housing_data.csv
大家可以在网上查找这个数据集，很好找到。

2.数据集中每一个属性的含义：

CRIM “numeric” 人均犯罪率

ZN “numeric” 超过2W5平方英尺的住宅用地所占比例

INDUS “numeric” 城市非零售业的商业用地比例

CHAS “integer” Charles河是否流经

NOX “numeric” 一氧化碳浓度

RM “numeric” 每栋住宅的平均房间数

AGE “numeric” 1940年以前建成的自住房比例

DIS “numeric” 到波士顿五个中心区域的加权平均距离

RAD “integer” 到达高速公路的便利指数

TAX “numeric” 每1W美元的全值财产税率

PIRATIO “numeric” 师生比

B “numeric” BK是黑人比例，越接近0.63越小，B=1000*（BK-0.63）^2

LSTAT “numeric” 低收入人口比例

MEDV “numeric” 自住房屋房价的平均房价单位为（1W美元）

3.导入数据

mydata<-read.table('D:/boston_housing_data.csv',

                   head=T,sep=','

                   ,stringsAsFactors = FALSE)

4.缺失值处理

首先使用is.na(mydata)，进行缺失值的处理，再使用代码na.omit(mydata)，删除缺失值，若不进行此步，就会出现错误提示：'x'里有无穷值或遗漏值。代码如下：

is.na(mydata) #查看是否有缺失值

newdata <- na.omit(mydata)  #删除缺失值

5.数据分析

在分析每一个属性之间的关联时，我在这里使用的是矩阵热图，首先引入corrplot函数包，将数据集变成相关系数矩阵：cor(newdata)，然后使用该包将相关系数热图显示出来

在图中，颜色越深代表两个关系中的相关系数越近，Boston的中位数房价（MEDV）一列中，与LSTAT、PTRATIO、RM等变量间的相关关系最大。

在这里矩阵图形默认为方形，也可以更改参数系数可以是圆形、方形、椭圆形、数值、阴影、颜色或饼图形，method = c("circle", "square", "ellipse", "number", "shade", "color", "pie")这些都是参数，现在可以将其改为椭圆形，代码：

corrplot(res, method = "ellipse",shade.col = NA, tl.col ="black", tl.srt = 45, order = "AOE")

显示图形如下图所示：

 

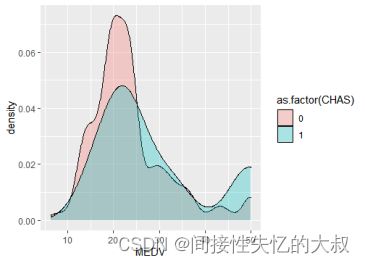
对表中参数发现有一个二值变量CHAS，在热度图中，它与其它属性的相关度都不是很大，CHAS是一个二值变量（即位于查尔斯河边记为1，否则记为0）。在这里我使用包ggplot2画图，图形如下图所示： 

通过图发现，CHAS=1时的房价分布与CHAS=2时房价分布基本相同。为了探究这一变量 对房价是否有显著影响，接下来将通过一系列检验方法验证。 将样本数据分为两个部分,CHAS=1为一组，CHAS=0为另一组。代码如下：

CHAS1<-subset(newdata,CHAS==1)

CHAS2<-subset(newdata,CHAS==0)

 6.样本检验

对于我个人来说，在我买房子的时候我首先看的是犯罪率，然后教育资源，空气质量和低收入人群，这四点对于我来说是比较重要的，犯罪率的高低可以直接影响房价，其余应该是属于间接性的，所以我对这几点先进行一个分析，代码如下：

somelist <- c(newdata$CRIM,newdata$PIRATIO,newdata$LSTAT,newdata$NOX)

colr <- c("blue","red","green","yellow")

plot(somelist,newdata$medv,col=colr,

     xlab = "影响因素",ylab = "房价")

我使用散点图进行分析，显示结果如下图所示：

可以发现在500~1250之间是对房价影响波动是最大的，人们更加重视的是犯罪率和空气质量，在达到1000时，房价有最高值。 

7.假设检验

通过Shapiro Wilk检验房价中位数是否服从正态分布。假设：

H0：房价中位数服从正态分布

H1：房价中位数不服从正态分布

代码：shapiro.test(scale(medv))，显示结果如下图所示：

由于P<0.001,拒绝原假设，即房价中位数数据不服从正态分布。

 

由于房价中位数不服从正态分布，因此采用Wilcoxn秩和检验方法检验在河边 的房价与不在河边的房价是否有显著差异。假设：

H0：在河边与不在河边的房价相同

H1：在河边与不在河边的房价不相同

代码：wilcox.test(CHAS1$MEDV,CHAS2$MEDV,alternative = "less")，结果如下图所示：

由于P>0.001，接受原假设，在河边的房价与不在河边的房价不具有显著差 异，因此在建立回归模型时考虑删除CHAS变量。

8.建立回归模型

代码：fit<-lm(medv~crim+zn+indus+nox+rm+dis+rad+tax+ptratio+b+lstat, data=newdata)

由其余变量来预测房价，使用summary()来查看描述统计量，显示结果如下图所示：

 

 9.异常值

使用car包作图，可以看出离群点，代码如下：

library(car)

influencePlot(fit, id.method="identify", main="Influence Plot", sub="Circle size is proportional to Cook's distance")

作图结果如下图所示：

如上图所示，纵坐标超过+2或小于–2的样本可被认为是离群点，水平轴超过 0.2或0.3的样本有高杠杆值。圆圈大小与影响成比例，圆圈很大的点可能强影响 点。下面用outlierTest()函数找到到具体离群值。代码如下，运行结果如下图所示：

outlierTest(fit)#求得最大标准化残差绝对值Bonferroni调整后的p值

 

连续使用outlierTest()函数检验得到所有异常点后进行删除。代码如下：

newdata<-newdata[-c(366,369,373,381,419,372,370,371,368,413,365),]

 10.检查共线性

vif(fit) #VIF值大于4表明存在多重共线性，如下图：

如上图结果所示，模型存在多重共线性，因此需要进行变量筛选。

11.变量选择

使用全子集回归，代码如下，显示结果如下图3-5所示：

leaps<-regsubsets(medv~crim+zn+indus+nox+rm+dis+rad+tax+ptratio+b+lstat,data=newdata, nbest=8)

plot(leaps, scale="adjr2")

上图结果表明删除变量CRIM,ZN,INDUS,RAD后的R方可以达到81%。

12.回归诊断 

 通过“残差拟合图”发现，残差值与拟合值存在一个曲线关系， 因此回归模型不满足线性假设。通过“正态Q-Q图”发现，图上的点应该落在呈45 度角的直线上，因此回归模型满足正态性。通过“位置尺度图”发现，图形显示非 水平趋势，因此回归模型不满足同方差性。接下来通过变量与房价中位数的散点图和核密度估计曲线判断变量之间的关系。如下图所示：

然后进行变量变换，改善模型效果，代码如下图所示： 

代码执行结果如下图所示：

 

可以发现一氧化氮浓度对房价的影响是趋于平缓的，每栋豪宅的房间数对房价的影响是上升趋势的，自建房比例对房价的影响不是很大，距离中心距离的距离越远，价格也是越低，对于师资比例来说，少的时候反而房价高一些，多了房价就下去了，对于犯罪率，犯罪率越高，房价越低，最高时，房子已经不值钱了。

总的来说，对房子价格的影响因素是多重的，二犯罪率对房价的影响最大，人们总是希望一个安全的地方成为自己的家园

 13.犯罪率对房价的影响

对此，犯罪率对房价也有很大的影响，可以使用直方图和散点图对两者之间的关系进行分析，如下图所示：

每个犯罪率对应的房价大概都呈正态分布，期望随着犯罪率的升高而降低，因为犯罪率越高，越没人敢住，自然没人买，房价就下降了。调查的地区大部分都在0附近，此处方差也比较大，波动较大，当CRIM>2时，方差比较稳定了。犯罪率在1~10之间的，地方还有几个地方房价很高，基本可以看作噪声。CRIM在25之后的地方数据量比较少。再查看直方图，发现332个地区都是犯罪率为0左右的。

 14.豪宅对房价的影响

首先查看散点图，代码如下：

plot(zn,medv)

如下图所示：

 

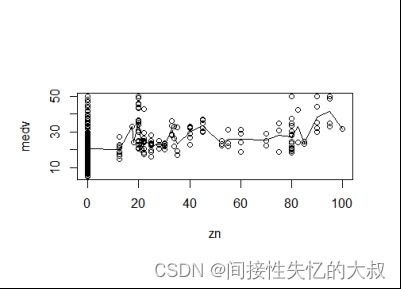
对上述的散点图添加一条趋势线，就可以很清晰的观察，代码如下：

lines(names(tapply(medv,zn,mean)),as.numeric(tapply(medv,zn,mean)));

显示结果如图所示：

 

 可以看到，大部分地区，豪宅都没有，房价在各个水平的变化基本都呈正态分布，且均值都相差不多，在85之后均值偏高，但数据量太小。所以基本可以认为此变量与房价没有关系。

15.商业用地对房价的影响

也是先查看商业用地与房价的散点图，可以得到大部分人都居住在18左右的地区，在0~4之间房价变化没有明显的规律（对样本进行一次观测，小概率事件基本不会发生，但房价在上下反复横条，所以很难说有规律），但如果把INDUS值分个类，按区间进行划分，可以想象出来，在每个区间基本是正太分布的，而且期望随着INDUS增加而降低直到INDUS达到8，之后降低的幅度不太大，甚至有些平稳。

代码如下：

plot(indus,medv)

length(unique(indus)); #计算INDUS变量有几种取值

tapply(medv,indus,mean); #各种取值的平均值

lines(names(tapply(medv,indus,mean)),as.numeric(tapply(medv,indus,mean)))#划线

运行结果如下图所示：

16.参考文献

[1] [美] 卡巴科弗（Robert I. Kabacoff） 著，王小宁，刘撷芯，黄俊文 等 译，《R语言实战》第二版，人民邮电出版社，2016-05-01，ISBN：9787115420572。

[2] 汪海波 著，《R语言统计分析与应用》，人民邮电出版社，2018-04-01，ISBN：9787115469823。

[3] 吴喜之 著，《多元统计分析——R与Python的实现》， 中国人民大学出版社，2019-01-01，ISBN：9787300266558。

[4] 薛薇 著，《R语言：大数据分析中的统计方法及应用》，电子工业出版社，2018-07-01，ISBN：9787121339158。

[5] 王斌会，《多元统计分析及R语言建模》(第五版)，暨南大学出版社，2016-03-01，ISBN：9787566817433。